
ローレンツ力による荷電粒子の運動問題
<この記事の内容>:前回扱った「電磁力とローレンツ力そしてフレミングの法則」の応用編です。
±の電荷(=荷電粒子)に働くローレンツ力によって、荷電粒子はさまざまな運動をします。
今回は例題を通して、それらの問題の解き方の手順やコツを紹介します。
<電磁気分野の予習・復習>:「高校物理/基礎(電磁気学)の解説記事総まとめ」左の記事でこれまでの電磁気シリーズの復習ができます。ぜひご利用ください。
目次(タップした所へ飛びます)
荷電粒子が受けるローレンツ力
この項では、まず”ローレンツ力の復習”を行い、次に→磁界が荷電粒子と垂直でない場合の力の向きと大きさの求め方を紹介します。
ローレンツ力の復習
さて、ローレンツ力とは正・負電荷が磁界の中を運動する際に受ける力でした。
$$その大きさは,f(N),q(C),v(m/s),B(T)$$
$$として:f=qvB\ldots (1)$$
で求めることができ、
さらに、その向きに関しては”フレミングの左手の法則”を用いて、
正電荷の時:
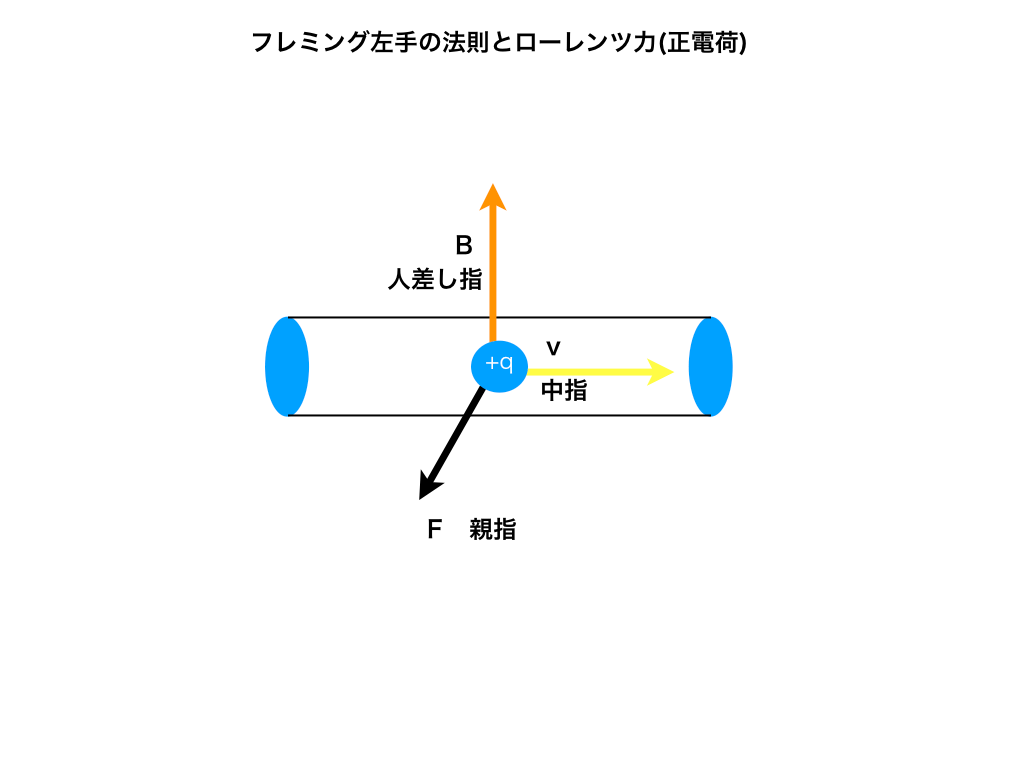
負電荷の時:
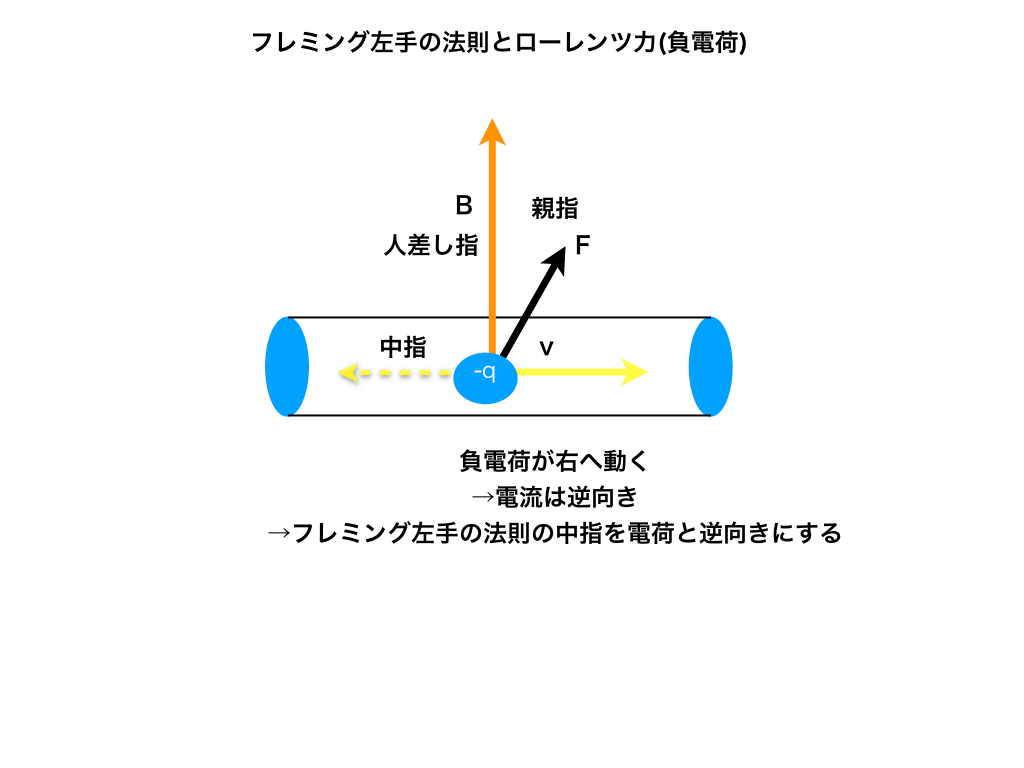
で定めることができました。「前回のローレンツ力の復習記事へ」<<さらに詳しくは左の記事を参照ください。
磁界と斜めに運動する荷電粒子
上の記事では、電荷の移動方向と磁界の向きが直交していました。
しかし、実際の入試問題などではこの2つがきっちり直交しない場合が非常に多いのです。
この項ではその際のローレンツ力の求め方を2stepで紹介します。
step1:速度の分解
そのようなときには、荷電粒子の速度vを磁場に”垂直な分”と“平行な分”に分解(ベクトルの分解)をします。
step2:三角比で分解した成分を求め公式に代入
そして、磁場⊥速度の成分だけを三角比を用いて計算し、①のBの値を変えることでローレンツ力f(N)を求めます。
これだけではイメージが湧きにくいかと思うので、具体的に見てみましょう。(参考:「物理で使う三角比とベクトルの基礎:力学・電磁気で困らないための数学」)
斜め方向への移動の具体例
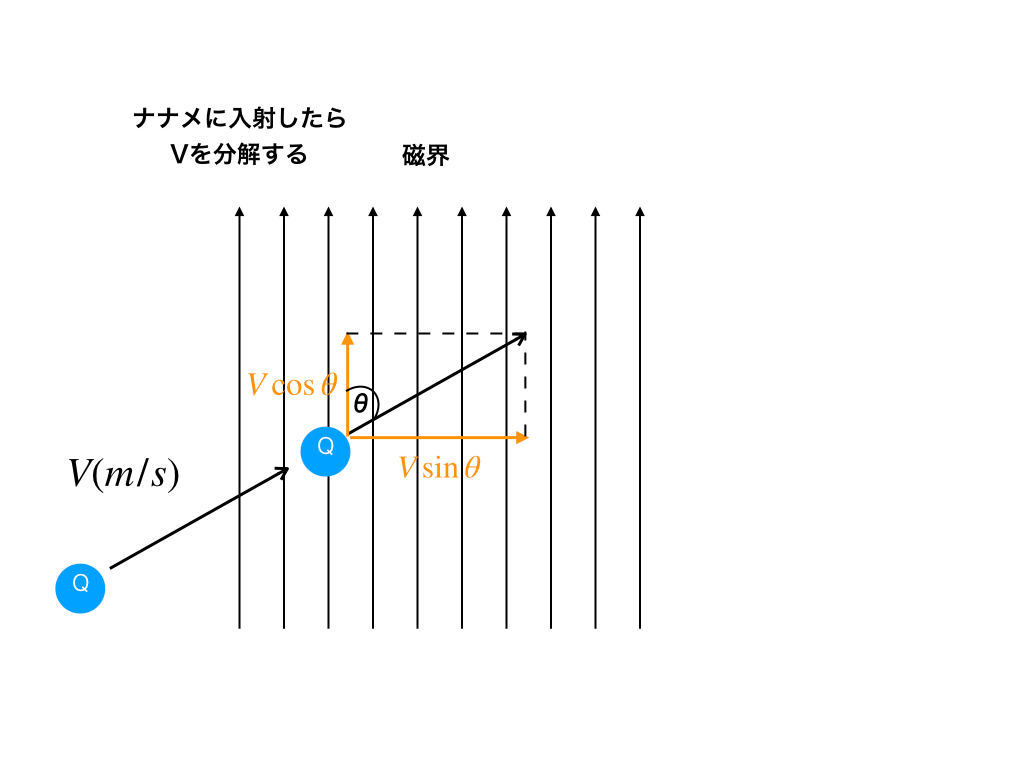
<図1:速度のうち斜め成分を分解する>
画面《上方向》へBがかかっており、そこにv(m/s)、+Q(C)の正電荷が磁場となす角θの向きへ進みます。
この際のローレンツ力を求めるためには、f=qvBの“vを分解して”磁場と垂直で影響をうける成分“v sinθ”のみを計算する事で
$$結果:f=qv\sinθB=qvB\sinθ$$
がこの荷電粒子が磁界から受ける力となります。
ローレンツ力と円運動
今回扱っているローレンツ力の運動の中でも、荷電粒子が等速円運動を行うタイプは頻出、かつ非常に重要なものです。
ここからは力学分野の復習を行いながら、典型的な例題を見て行きます。
等速円運動の復習
等速円運動とは、「力学:単振動の解説step0-2」で解説していますが、文字通り”同じ速度で”円運動することです。
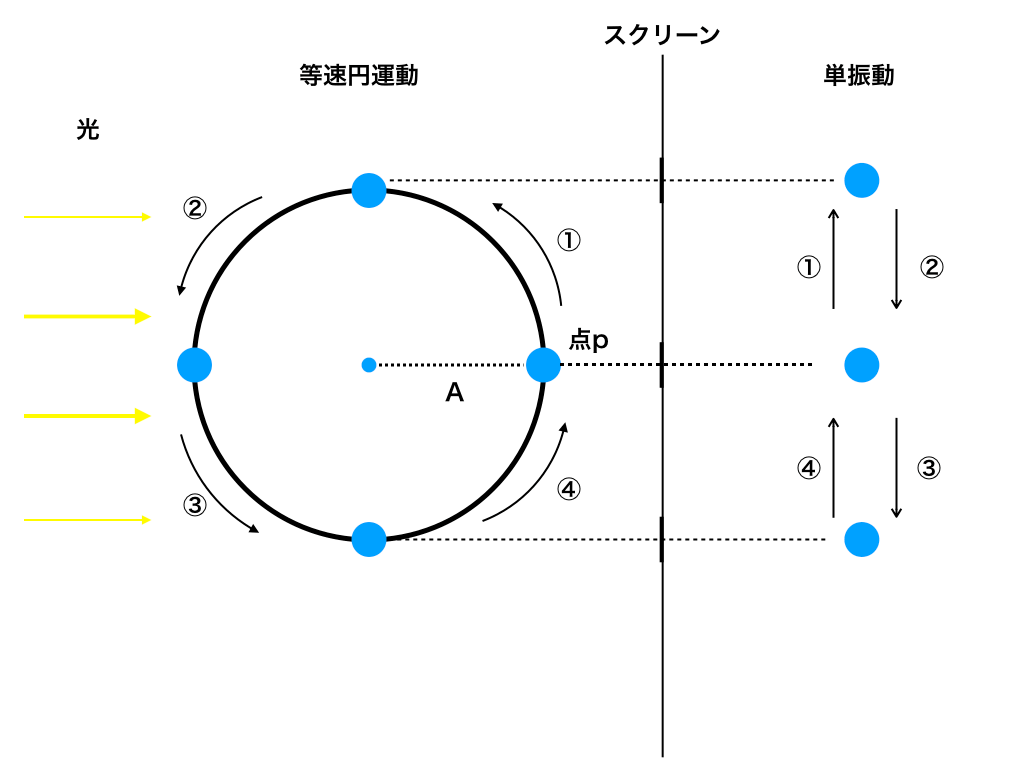
<円運動1の様子(と単振動)>
ここで、角速度ωとv、加速度aの関係は以下の図のようになります。
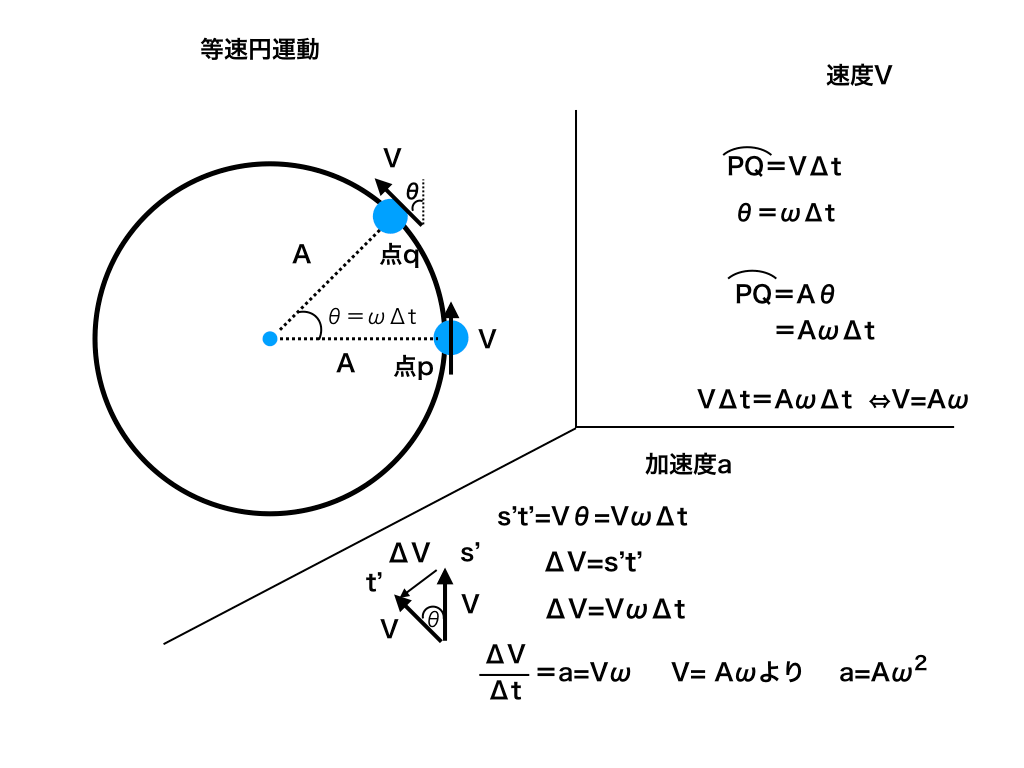
<等速円運動2>
荷電粒子と円運動
実際に確認問題を通して学んで行きます。
ここで扱う問題は基礎的ですが、荷電粒子が磁界だけでなく電場の影響を受ける事によって、3次元空間中をらせん運動するような応用問題に発展していきます。
問題
以下の図1のようにq(C)で質量m(g)の正電荷aが、点Oを中心、半径Rで反時計回りの等速円運動をしている。
磁場B(H)が図の奥から手前にかかっているとき、この円運動の
(一):向心力F
(二):角速度ω
(三):周期T
をそれぞれ求めよ。
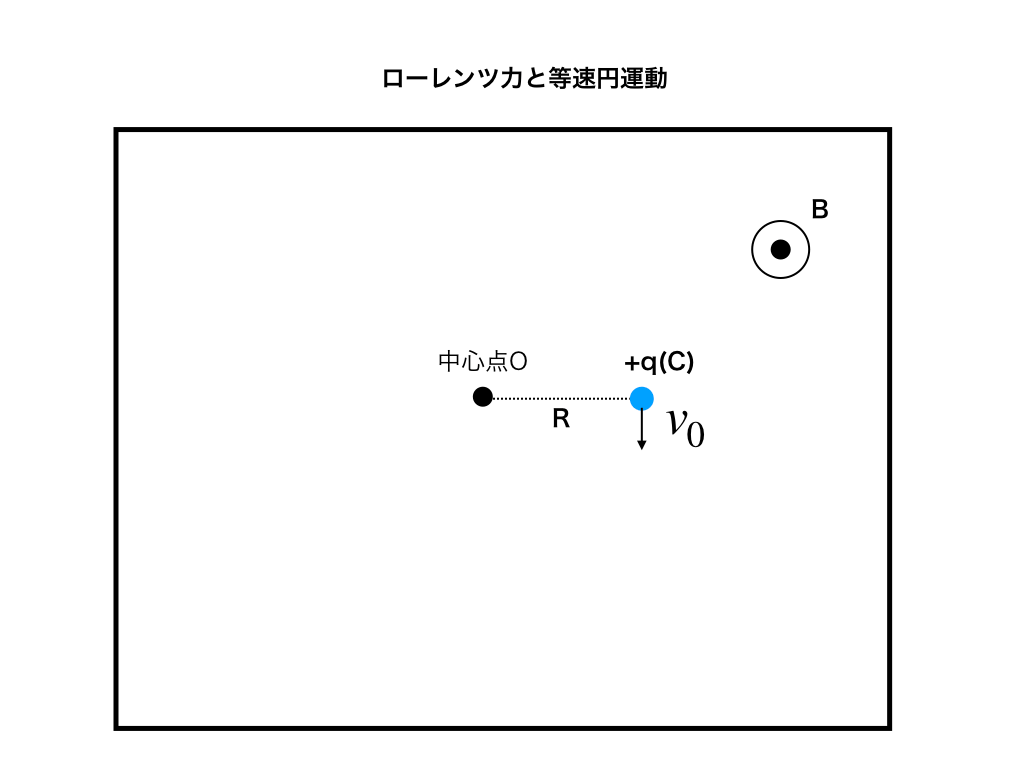
<問題図1>
解法と解説
次のように、フレミング左手の法則よりローレンツ力は常に中心点Oに向かって働きます。
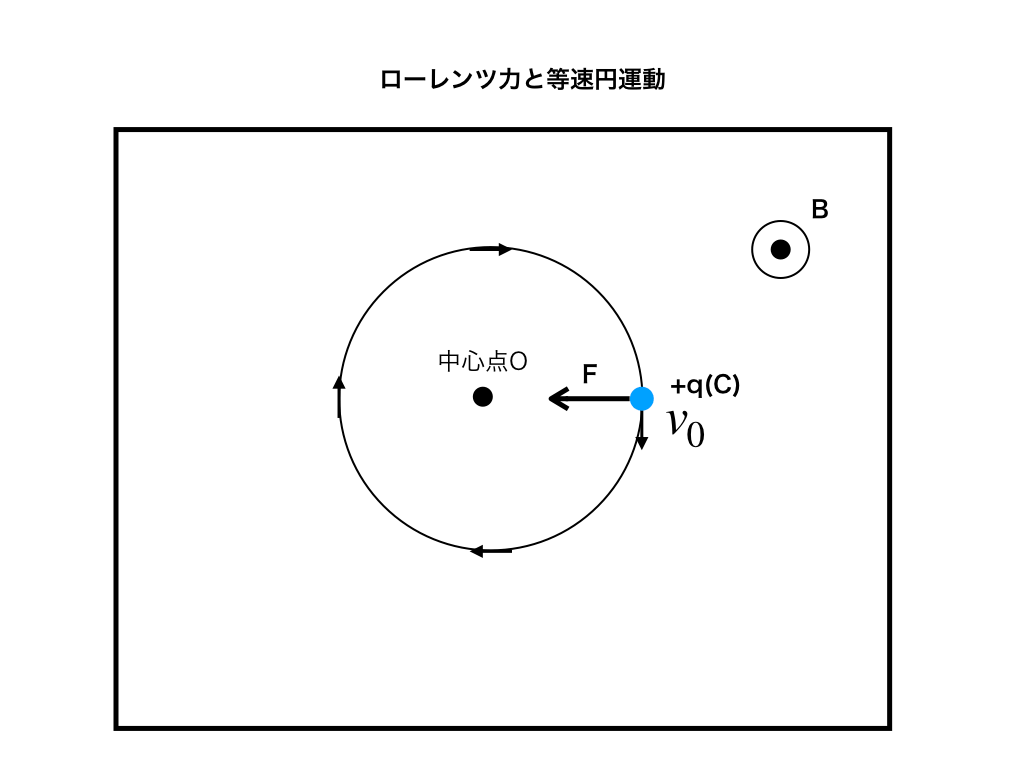
<向心力がローレンツ力の円運動>
すなわちこのローレンツ力が向心力であるので
$$(解答一):向心力F=qv_{0}B$$
角速度ω(rad/s)は単位を見るとわかるように、1秒あたりに進む弧度(ラジアン)を意味します。
(参考記事:「弧度法を徹底解説!度数法との違いや注意点」)
<図2>にある様にV=A(半径)・ωの式を使ってこの円運動は$$ω=\frac{V_{0}}{R}(rad/s)$$で計算出来ました。
(解答3):$$周期T=\frac{2\pi}{\omega}$$より、$$T=\frac{2π}{\frac{V_{0}}{R}}⇔\frac{2πR}{V_{0}}$$
まとめと次回へ
このようにして、荷電粒子の運動を介して力学分野と電磁気分野を融合させた問題は(特に難関校になるに連れて)頻出します。
ここではその基礎の基礎を学びました。
次回は、「荷電粒子の運動(応用編)」として、先ほど述べた3次元での“らせん運動”や電場の影響を受ける運動などを扱います。
電磁気分野の関連記事一覧
これまでの電気分野の記事は「高校物理・物理基礎の電磁気学総まとめ!」よりご覧ください。
<磁気分野:第1回>:「電流が作る磁界の向きと大きさを求めるコツ」
<第2回>:「フレミング左手の法則と電磁力/ローレンツ力の関係」
<第3回>:「今ここです」
<第4回>:「(予定)荷電粒子の運動(応用)らせん運動+α」
「スマナビング!」では、読者の皆さんのご意見やご感想の募集を行なっています。
ぜひコメント欄までお寄せください。

