
コンデンサーの仕組みと公式を理解しよう!(1)
コンデンサーの分野はただ公式を暗記しておけば良い、と言うわけではありません。
それぞれの公式には意味があり、コンデンサーの仕組みを理解することで自然と公式が頭に残ります。
「電池のした仕事」や「静電エネルギー」が苦手という人も多いですが、
これらも力学と対応させて考えることで理解しやすくなります。
*2019年12月12日加筆・更新
目次(タップした所へ飛びます)
コンデンサーの仕組みと公式
・(準備編)電場と電気力線のおさらい
・電池の役割と電流&コンデンサーが電気を貯める流れ
・コンデンサーが電気を貯めておける理由
・電気容量の公式
・Q=CV
・静電エネルギー(要注意!)
・電池のした仕事
(準備編)電場と電気力線のおさらい
今回は、コンデンサーの仕組みや公式の意味など理論編を解説して行きます。
以前の「ガウスの法則と電場・電気力線について」解説した記事を既読として進めるので、
まだ読んでいない方はぜひ先にご覧下さい。
電池の役割と電流&コンデンサーが電気を貯める流れ
さて、電池はコンデンサーを含む回路でどの様な役割を担って居るのでしょうか?
よく電池はポンプに例えられます。電圧の低いところから高いところへ電流を持ち(汲み)上げるからです。
実際には、電流は電子と逆向きに進みます。<追記:「電流とは何か?向きやI=envSの公式をわかりやすく解説」>
電池のプラス極側からマイナス極を経由して、電子が下側のコンデンサー板に集まります。
一方で、電池のプラス極と接続している上側のコンデンサー板(金属)は、相対的に電子<陽子となります。
結果的に、上側の金属板には”正の電荷+Q”を帯び、下側の金属板は”負の電荷-Q”を帯びることになります。
コンデンサーが電気を貯めておける理由
電池を外した後も、コンデンサーは電気をある程度貯めておけます。
それは、上側極板の正電荷と下側極板の負電荷がクーロン力(静電気力)で引き合っているからです。
電気容量C(単位F:ファラド)の公式の理解
では、1つ目の公式C=ε0S/dの式の意味を考えてみます。
電気容量は、そのコンデンサーがどれだけの電気を蓄えられるか、
その能力の大きさの様なものを表しています。
ここでのε0は真空中の誘電率で、単位は(F/m)、Sは極板の面積(m2)、dが極板間の距離(m)です。
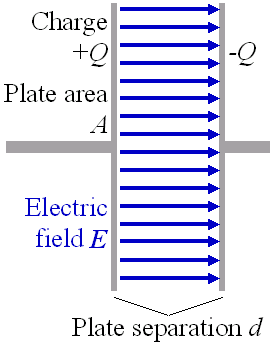
<図1>
$$C=\frac {\varepsilon _{0}S}{d}( F) $$
よく考えるとわかるのですが、コンデンサーは両極板間の“クーロン力”で電気を貯めて(引き止めて)いました。
$$<参考:クーロン力の公式F=ε_{0}\frac{qQ}{r^{2}} ,>$$
(rは電荷どうしの距離、ここではd)
つまり極板の面積が広ければ広い程、たくさんの陽子や電子を極板に並べることができます。
結果としてより強い力(=クーロン力)で極板同士が引き合い、
電荷を引き止めておける=沢山電気を貯める事が出来ます。
一方で極板間の距離が広いと、クーロン力は弱くなるので電荷を引き止める力が弱くなり、
結果として電気容量は小さくなります。
この様な理由で「電気容量は、極板の面積に比例し、極板間の距離に反比例する」と言えます。
電気容量についてさらに詳しく→コンデンサーの電気容量を徹底的に(コンデンサ第2回)
コンデンサーに蓄えられる電気量の重要公式
Q=CV
この式は、Q(電気量:単位C「クーロン」)は電気容量C(単位F)×電圧(単位V)を意味します。
電気量Qは、コンデンサーの電気容量Cを定数としてVに比例する。
つまり『電圧の値が大きければ大きいほど』また、『電気容量が大きければ大きいほど沢山の電気を貯める事ができる』という事を言っているわけです。
静電エネルギー
コンデンサーは、【静電エネルギー】というエネルギーを持っています。
これは、力学の位置エネルギーに似ているので、この二つを対応させながら見てみます。
力学においての位置エネルギーとは、重力に逆らって物体を持ち上げた仕事と等しい値になりました。
物体の質量をm(kg)、重力加速度をg(m/s2)、高さをh(m)とすると、
重力に逆らって外力がした仕事W=位置エネルギーU=mghと表せます。
一方で電気の世界では、Vが「電位(差):電気的な高さ」、Eが「電場:電気的な傾き」、qが「電荷の大きさ」と考える事が出来ます。
これについては→「電位と電場の違いを図と計算でイメージする」で詳しく解説しています。
また、コンデンサーの極板間距離をd(m)とすると、
クーロン力に逆らって下側極板から上側極板まで運ぶので、
(力学の世界)F=mg : U(力学の位置エネルギー)=mgh
(電気の世界)F=EQ :U(静電エネルギー)=Fd=EQd
ここでV=Edを代入すると、U=QV、、、とする人が多いのですが、
実際の静電エネルギーはU=(QV)/2 になるのです。
どこで間違えたのでしょうか??
先ほどからFに逆らってdだけ電荷を運ぶとして、(U=)W=Fd と計算していましたが、
そのF(クーロン力)を作り出すのは電場:Eでした。
そしてその電場を作り出すのは、上下の極板に存在する電荷±Qだったわけです。
しかしよく考えるとコンデンサーは初めから±Q(C)の電荷を持っていたわけではありません。
充電前は0(C)だったものが、徐々に電荷が増えて最終的にQ(C)になっただけです。
その最後の状態で計算したためU=QV という誤った答えを導いてしまったわけです。
正しい静電エネルギーの求め方
ではどうすれば正しく静電エネルギーを求められるのでしょうか。
それは、Q(C)を微小なq(C)を集めたものと考えることで解決できます。
初めV=0、E=0の時にqをdだけ持ち上げた時の仕事は0(J)です。
次にq(C)をdだけ持ち上げる時には、先ほどのq(C)によって少しだけ電場が生じています。
この時の電場をE’とすると、2番目の時の仕事はW=E'qdとなります。
この仕事を上下の極板が±Qの電荷をもつまで行います。これを図で考えてみます。↓
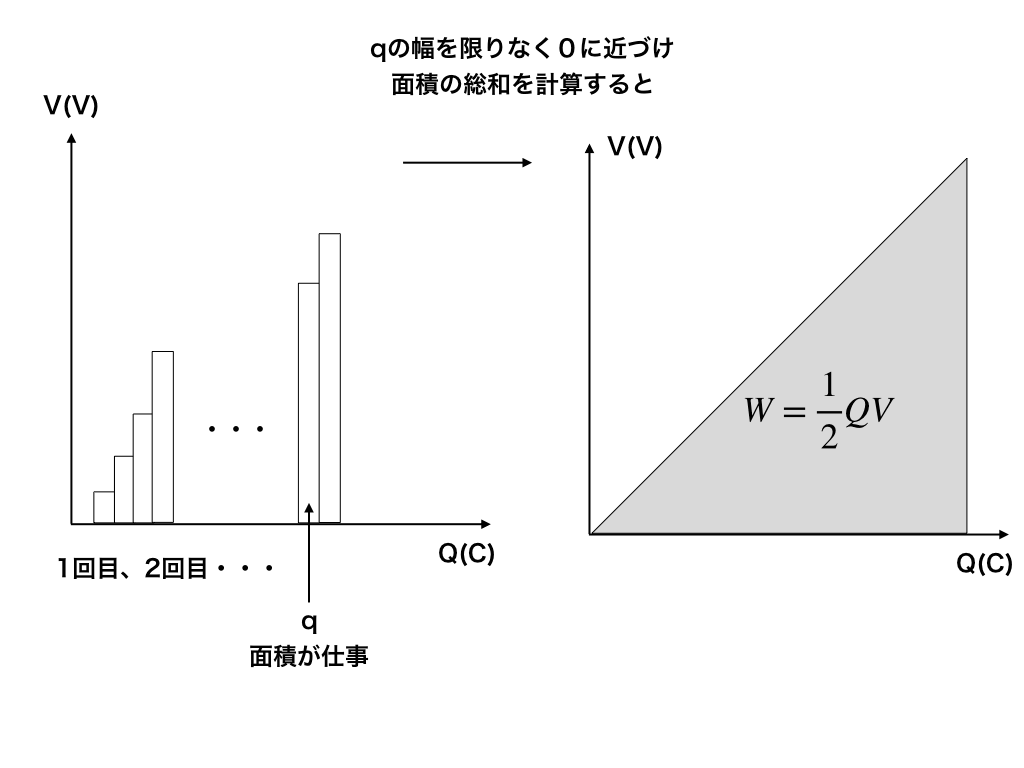
<図2>
<図2>の様に右のグラフの三角形の部分がW=Uとなる為、U=1/2(QV)となります。
係数に1/2がつく訳が分かって頂けたでしょうか?
電池のした仕事
コンデンサーの静電エネルギーは1/2(QV)でした。
この時電池はQ(C)をV(V)運んでいるので、その仕事はW=QV となります。
このエネルギーの差は、主に回路中の抵抗などから発生する【ジュール熱】が原因です。
コンデンサーの電気容量の解説記事へ
沢山単位や公式が出てきましたが、いずれも意味を考えると当然なものばかりです。
忘れても思い出せる様にしっかり意味を理解するようにしておいてください。
次回は、コンデンサーの直列/並列接続による電気容量の変化、誘電体の挿入を取り上げます。
コンデンサの続編記事と電磁気まとめ
第2回upしました。→コンデンサーの電気容量を徹底的に(コンデンサーシリーズ2)
「電磁気の解説記事総まとめページ」<<物理・物理基礎の「電磁気」分野でわからない所があれば、このページで探してみてください!
質問、誤植、記事リクエストその他お問い合わせはコメント欄までお願いいたします。

