
三角方程式の例題と解法解説一覧
この記事では、三角比・三角関数の公式やテクニックなどをフルに利用して、
「三角方程式」の問題のタイプごとの解き方のコツを解説しています。
三角比・三角関数の公式の復習にもなるので、ぜひ全タイプを確実に解けるようにしておきましょう。
目次(タップした所へ飛びます)
三角方程式の出題パターンまとめ
(三角方程式とは?:三角方程式は、xの式で表される通常の方程式の代わりに三角関数が入っているものです。他にも、積分の形が入った「積分方程式」や「微分方程式」、「指数・対数方程式」などがよく出題されます。)
>>「色々な方程式/不等式の解き方の解説記事まとめ」<<
ここから、三角方程式を解くための公式のタイプごとに、例題→解説(と関連する記事のリンク)を並べていきます。
途中であいまいな公式などがあった時は、すぐにリンクから関連記事へ行って確認して下さい。
(※:先に三角比・関数の公式を確認したい人は→「三角関数の公式一覧:理解して覚える方法」よりご覧ください。
置き換えを利用する三角方程式(Type1)
最も基本的な「置き換え」を利用するタイプから始めましょう。
sin2θ +2sinθ+1=0 (0≦θ<2π )
この程度であれば置きかえずに因数分解して解けるかと思いますが、
一応:sinθ=t と置いてといていきます。
三角関数を置換する時の注意事項
ここでθの条件より、tに置換するときtが動ける範囲に制限が加わる事に注意が必要です。
0≦θ <2π のもとで、-1≦sinθ ≦1を動くので、(-1≦t≦1)
よって、与式は、t2+2t+1=0 (-1≦t≦1) となります。
ここで、因数分解を行なって、<参考:「因数分解の公式と解き方のコツ」>
(t+1)2=0
よって、t=ー1
次に、t=sinθが求まったので、θも求まります。
sinθ=-1 ,(0≦θ <2π )の条件を満たすθは3π/2のみなので、
解答:θ= 3π/2
三角比の相互関係を使うタイプ(type2)
三角比・三角関数の相互関係について、少しだけ復習しておきましょう。

<三角関数・三角比の相互関係1〜3>
これらをうまく利用して、解法1の形に持っていくことを考えます。
$$(問2):2\sin ^{2}θ+3\cosθ -3=0 、(0\leq θ <2\pi )$$
のとき、θの値を求めよ。
(解答2)与式にcosθがあるので、三角比・三角関数の相互関係を利用して、sin2θをcosθの形に変形することを考えます。
三角関数の相互関係より、$$\sin^{2}\theta =(1-\cos^{2}\theta )$$
$$2(1-\cos^{2}\theta) +3\cos\theta -3=0$$
$$-2\cos^{2}\theta +3\cos\theta -1=0$$
これで、コサインに揃ったので、
$$2\cos^{2}\theta -3\cos\theta +1=0$$
このままたすき掛けします。
(2cosθ -1)(cosθ -1)=0
したがって、方程式の解はcosθ =1/2,1
ここで、
cosθ=1/2のときのθがすぐに分からなければ、単位円を描いて考えると便利です。
(単位円を使ってθを求める手法は、次回紹介する『三角不等式』を解く際に大変役立ちます。)
単位円を使ってθを求める
くわしくは、「三角関数の還元公式(sin(θ±π)やcos(θ±1/2 π)」の記事で使い方などを紹介しているので、
よければ参考にして下さい。
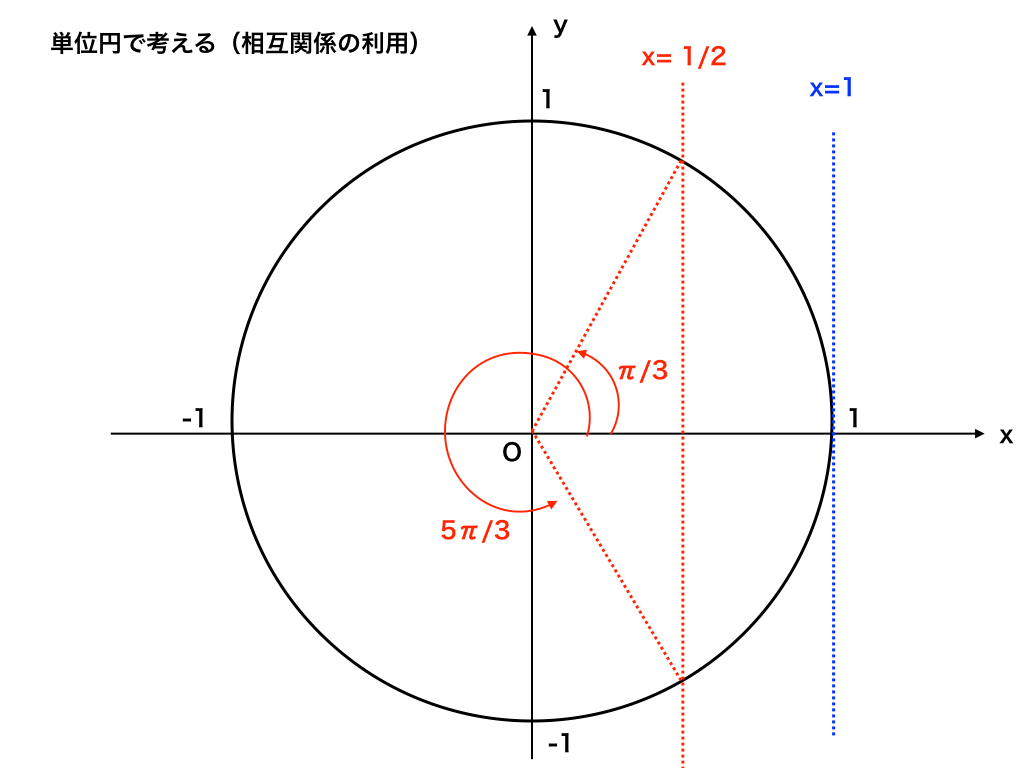
<図:単位円を使ってθを求める1(相互関係の利用)>
$$ゆえに、θ=0,\frac{\pi}{3},\frac{5}{3}\pi$$
2倍角の公式を利用する(type3)
二倍角の公式を利用するタイプ。(解法3)
これらは三角関数の加法定理からすぐに導けるので(下リンク参照)自然に覚えてしまうまでは、
なるべく導出してから使う方が良いです。

<図:三角関数の倍角公式>
では例題に取り組みましょう。
コサインの2倍角を利用する(要注意)
(問3)以下の三角方程式、
cos 2θ-3sinθ-2=0 、(0≦θ<2π )の時、θを求めよ。
cosの2倍角の公式を使う問題です。
cos 2θ-3sin θ-2=0; 与式より、-3sinθがあることから、
コサインの形を消してサインに揃える事を考えます。
つまり、cos 2θ=1-2sin2θの二倍角の公式を使います
cos 2θ-3sin θ-2=0
1-2sin2θ-3sinθ-2=0
両辺に(-1)をかけて整理すると、
2sin2θ+3sinθ+1=0 となります。
<ここでは、sinθ=tと置かずに直接たすき掛けをして因数分解します>
(2sinθ+1)(sinθ+1)=0、 従って、方程式の解:sinθ=-1,-1/2
ここで、再び単位円を使って、
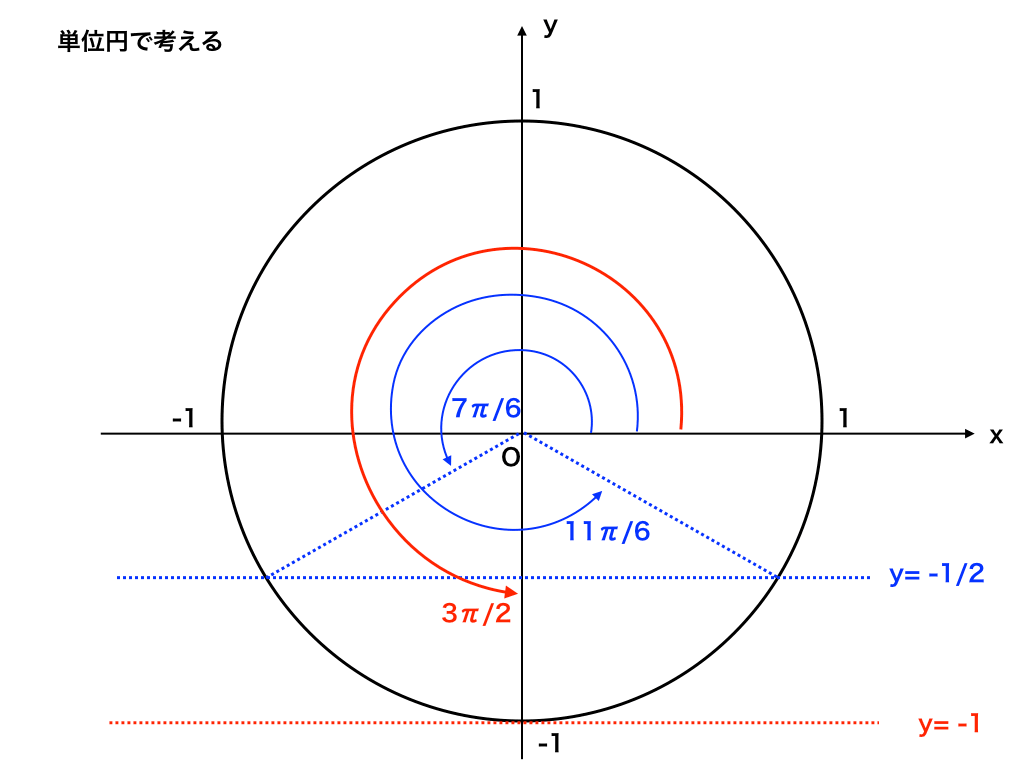
<上図:単位円を使ってθを求める2>
$$従って、θ=\frac{7}{6}\pi ,\frac{11}{6}\pi ,\frac{3}{2}\pi,$$であることが分かります。
三角関数の二倍角の中でもコサインの公式は数が3つあり、出題されやすいです。
どの形に変形すると良いか、よく類題などをといて身につけましょう。
三角関数の合成の利用(type4)
この項では、三角関数の合成を使って三角方程式を解いていきます。
・合成の仕方を公式で覚えてしまっている人
・cos型で合成できない人
は先に、必ず↓の記事をご覧ください。
(問4)$$\sqrt{3} \sinθ +\cosθ-1=0 ,(0≦θ<2\pi )$$
の時のθを求めよ。
サイン型で三角関数を合成;θの範囲に注意
sin型で合成して、式を整理すると$$2\sin (θ+\frac{π}{6})=1$$
ここで、(θ)の部分が(θ+π/6)に変化していることに注意して、
$$\frac{π}{6}≦θ+\frac{π}{6}<2π+\frac{π}{6}=\frac{13}{6}π$$
簡単にするために、(θ+π/6)=θ'とおきます。
$$\frac{π}{6}≦θ'<\frac{13}{6}π$$
sin(θ')=1/2
ここで、単位円を描いて
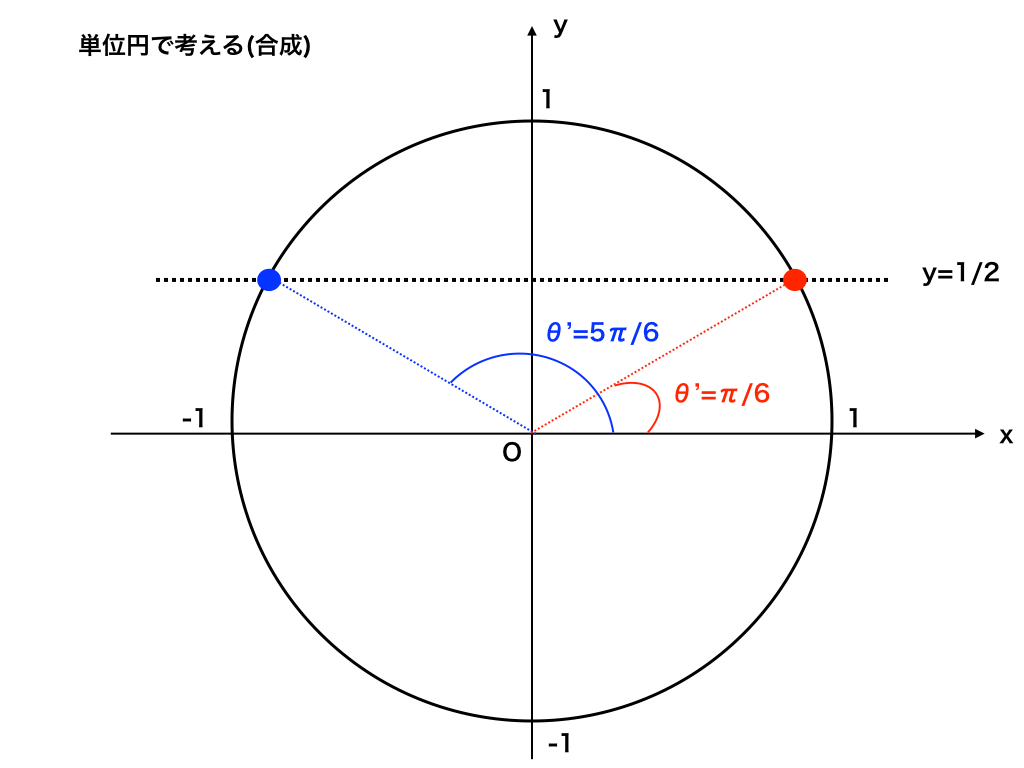
<単位円(三角関数の合成バージョン)>
θ'=π/6と、5π/6ここで、θ+π/6=θ'だったので、
$$(答)θ=0,\frac{2π}{3}$$
三角方程式のまとめと三角比・三角関数の記事
・今回の記事では比較的簡単な三角方程式を紹介しました。
・三角比の相互関係や三角関数の公式を知っているだけでなく、うまく式変形して方程式が解けるように類題などを探して練習してみて下さい。
関連記事(三角比・三角関数)
次回は、続編として『三角関数が入った不等式の解き方』を扱います。(NEW!)
(三角関数の公式・相互関係のまとめ&いろいろな方程式・不等式)
>>「三角関数の公式は覚えず導く!公式シリーズまとめ」<<
>>「高校数学で学ぶ方程式・不等式の解き方総まとめ!」<<
今回もご覧いただき有難うございました。
このサイト(『スマホで学ぶサイト、スマナビング!』)では、皆さんのご意見や、
記事リクエスト、などをもとに日々改善・記事追加更新を行なっています。
そこで
・記事のリクエストと質問・ご意見はコメント欄にお寄せください。
・また、多くの学生・受験生に利用して頂くためにSNSでシェア(拡散)&スマナビング公式Twitterのフォローをして頂くと助かります!
・より良いサイト運営・記事作成の為 ぜひご協力をお願いします。
・その他のお問い合わせ/ご依頼は、お問い合わせページよりお願い致します。

