
<因数分解のやり方をこの1記事でマスター>
数学の計算や、問題を解いていく上で「基本中の基本」となる『因数分解』ですが、数Ⅲや数ⅡBで点数が取れないことの根本原因が、因数分解などの基礎事項であった、ということは非常に多いのです。
ぜひこの記事をじっくり読んで、因数分解の基本から、そのほかの分野にも応用できる『工夫』までしっかりと身につけて下さい。
目次(タップした所へ飛びます)
因数分解の仕方・方針
まずは、因数分解の基本的な公式から復習していきます。
因数分解の基本公式
今後数え切れないほど使う公式ばかりです。もう一度確認しておきましょう。
\(x^{2}+2ax+a^{2}=(x+a)^{2}\)
\(x^{2}-2ax+a^{2}=(x-a)^{2}\)
\(x^{3}+3ax^{2}+3a^{2}x+a^{3}=(x+a)^{3}\)
\(x^{3}-3ax^{2}+3a^{2}x-a^{3}=(x-a)^{3}\)
上の4つは二項定理で導くことが出来ます。
>>「二項定理とは?その仕組みとCを使う理由」を読む
\(x^{2}-a^{2}=(x+a)(x-a)\)
\(x^{3}+a^{3}=(x+a)(x^{2}-ax+a^{2})\)
\(x^{3}-a^{3}=(x-a)(x^{2}+ax+a^{2})\)
たすきがけの利用
基本公式をおさえたら、次はたすき掛けをみていきましょう。
襷(たすき)のように”ななめ”に掛け合わせて、因数分解する式のかたちに戻るように計算するのがたすき掛けです。<図2>
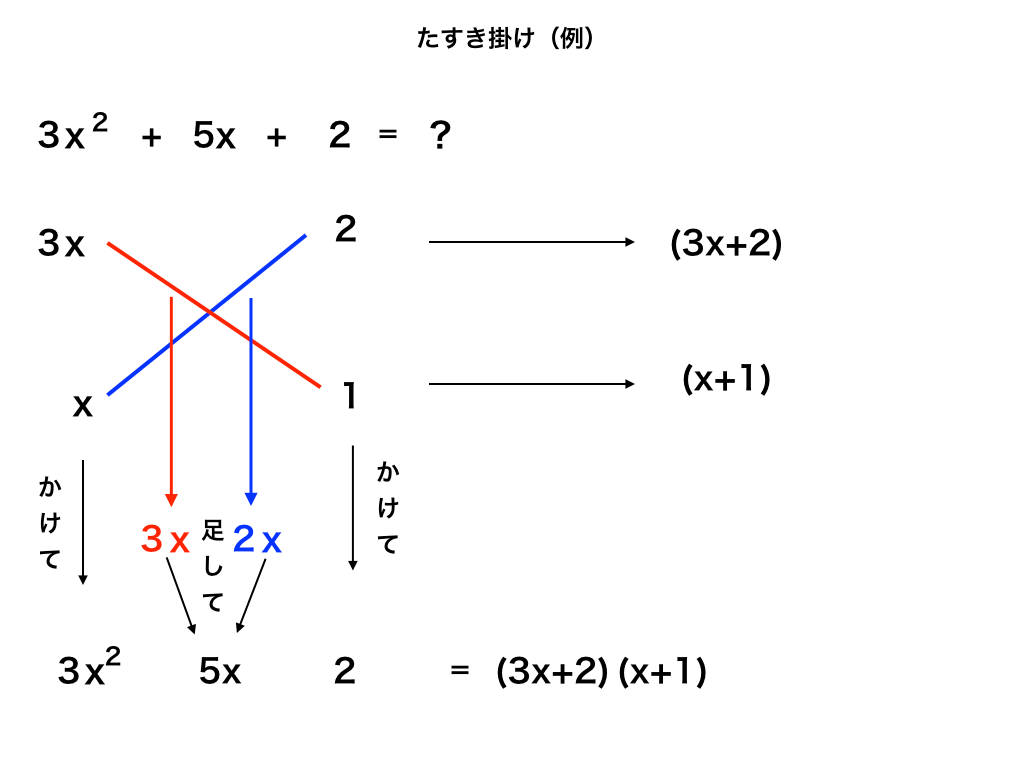
<図2>上の例をつかって『たすきがけの手順』を確認しておきましょう。
例)\(3x^{2}+5x+2\)を因数分解せよ。
まず与式の\(3x^{2}+5x+2\)のx2の係数を見ると「3」です。
ここで、(3x〜△)(x〜△)・・・(※1)の形にしか因数分解できないことがわかるかと思います。
次に定数項の数は「2」なので、
x2のときと同様に考えると、(◯〜2)(◯〜1)・・・(※2)
に因数分解されることになります。あとは、(※1)と(※2)を組み合わせて、
xの係数が「5」になるようにたすき掛けをすることで、(3x+2)(x+1)になリます。
因数分解をする工夫と手順<公式が使えない時>
ここからが本番です。以下の3つの工夫 +因数定理の利用は、因数分解を解くことだけでなく、
他のいろいろな分野の問題でも【解決の糸口】になる重要なものばかりです。
知らないものや、忘れているものがあればぜひ頭にインプットしておいて下さい!
さらに、これらは単独で使うだけでなく、
複数の工夫を組み合わせて使う場合があるので、よく練習しておく必要があります。
手順1:次数の低い文字でくくる
高次方程式や、複数の文字の式を因数分解する際に有効な手法です。
\(例1)a^{2}+ac+2ab+b^{2}+bc\) を因数分解せよ。
この式の中で、一番次数が低い文字は“c”です。そこで、まず"c"でくくってみます。
\(c(a+b)+a^{2}+2ab+b^{2}\)すると、
cが掛かっていない部分がちょうど\((a+b)^{2}\)に因数分解できるので、与式=c(a+b)+(a+b)2
次に、c(a+b)と(a+b)2には共通の(a+b)があるので、(a+b)でくくってあげると、
\(=(a+b)\cdot {c+(a+b)}\)
よって、与式=(a+b)(a+b+c)と因数分解できます。
手順2:置き換えを行う
「置き換え」という手法は、次数が大きい式で次数下げ(参考:「次数下げの方法とテクニック【計算ミス防止+高速化】」)のために行うのはもちろん、
・三角関数の方程式(→「三角関数が含まれる方程式の解き方と工夫」)や、
・指数・対数方程式などでも頻繁に使う方法です。
(例題):\(x^{4}+2x^{2}+1\)を因数分解せよ。
\(x^{2}=tとおくと、与式はt^{2}+2t+1\)とおきかえることができます。
ここで\(t^{2}+2t+1は、(t+1)^{2}\)に因数分解出来ます。
最後に、t=x2であったので、tに代入すると\((x^{2}+1)^{2}\)。
よって、\(与式=(x^{2}+1)^{2}\)となります。
置き換え時の注意事項
このように、大変便利な『置き換え=新しい文字で表す』方法ですが、1つ慎重に扱わないといけないことがあります。
それが、新しい文字に置き換えた時に、置換した文字に「範囲」という条件がつく事があるという事です。
(例:\(\sin \theta =t ,0≦\theta≦2\pi\)とするならば、-1≦t≦1 )など。
(この記事での因数分解ではそれほど考慮する必要はありませんが、非常によくあるミスなので頭の片隅に置いておいて下さい。)
手順3:(二乗)ー(二乗)を無理やり作り出す
これは、先ほどの基本公式で紹介した、\(x^{2}-a^{2}=(x+a)(x-a)\)
のカタチに持ち込む方法です。具体例を見た方が理解しやすいので、例題2の式を使って解説します。
(例題2):x4+4を因数分解せよ。
\(x^{4}+4が、x^{4}+4x^{2}+4\)であれば(2)で紹介したように因数分解できます。
そういった場合に気付いたら、“無理矢理”
\(x^{4}+4x^{2}+4\)を作り出してみます。
具体的には、\((x^{4}+4x^{2}+4)-4x^{2}、\)
つまり、”-4x2 ”の部分で帳尻を合わせます。
\((x^{2}+2)^{2}-4x^{2}=((x^{2}+2)-2x)(x^{2}+2+2x)\)
これをきれいな式にすると、
\((与式)=(x^{2}+2x+2)(x^{2}-2x+2)\)となります。
因数定理を用いる(剰余の定理の特別な場合)【応用レベル】
さて、基本的な公式も使えず、たすき掛けも難しいような場合には『因数定理と剰余の定理』を利用すると因数分解できる場合があります。
剰余の定理と因数定理について
f(x) =(xの式)で表されるとき、f(x)を(x-α)で割った商をA(x)、あまりをBとすると、f(x)は以下のように表せます。
f(x) =( x-α)A(x) +B:(余りBは、わる式(xーα)よりも次数が低いので定数項となります。)
ここで、xにαを代入してみると、\(f(α) =(\alpha -\alpha)A(α)+B\)
\(ここで、(\alpha -\alpha) A(α)\)の部分が0になるので、f(α) =B となります。
さらに、この余りBが0になる時を考えてみましょう。
つまり、(x-α)でf(x)が割り切れるならば、
f(x)=(xの式)のxにαを代入すると、f(α)=0と言えるのです。
このことを応用してみます。
以下の例題4のように、式のxに適当な数字を代入して0になるものを探していきます。
具体例とちょっとしたコツ
\(例題4)x^{4}-2x^{3}+x^{2}-x-2 \)を因数分解せよ。
※:上の項で”適当な数字を代入して式=0になるものを探す"と書きましたが、最短でその数にたどり着くにはあてずっぽうに代入するのではなく、$$\pm\frac{定数項 (ここでは-2)の約数}{最高次(ここではxの4乗)の係数の約数}$$の中から代入していきます。
(※):このコツについて、詳しい使い方となぜ成り立つのかを証明した記事は
>>「n次方程式の解を見つける方法とその証明」<<で解説しています。
つまり、±1,±2を入れていくと、x=2を代入した時に、
(与式)=24-2×23+22-2-2=0 、となるので先ほど解説した因数定理より、
この式は(x-2)を因数に持ちます。このことから、式を(x-2)で割っていくと、
\((x-2)(x^{3}+x+1)\)と因数分解できます。
まとめと因数分解の整数問題への応用
・因数分解の基本公式と、二項定理をマスターする>>
(参考):「二項定理の公式の意味とCを使う理由」<<
・因数分解を利用して、うまく整数問題(+不定方程式)を解くコツをまとめた記事を作成しました。
>>「整数問題の解法とコツ:因数分解と絞り込み利用型」<<
>>「不定方程式の解き方(因数分解利用編)」<<
・上で紹介した工夫+因数定理を類題を、『実際に手を動かして』出来るだけ多く解く事で身につける
・特に数学Ⅲの微積分など、レベルが上がった問題で、思うように得点出来ない時は基本に立ち返る!
↑最重要ポイントです!↑

