還元公式は覚えるな!簡単な導出法を2種類紹介します
この記事では三角関数の還元公式の覚え方に悩んでいる人を対象に、最小限の記憶で、その場で導く方法を2ステップで紹介しています。
なるべく覚える量を減らしつつ、たった2ステップでどんな三角比・三角関数の還元公式の問題も解けるように解説しているので、ぜひ
最後までご覧ください。
2018/11/26更新。「還元公式を加法定理で攻略する方法」を追記しました。
目次(タップした所へ飛びます)
三角関数/三角比の還元公式(余角/補角/負角の公式)の覚え方







数1の図形と計量、数2の三角関数、そして数3の極限・微分・積分まで、三角関数は大学受験数学に於いて、文系・理系問わず最重要の関数です。
しかし、
- 覚えるべき公式が多い
- 途中で躓いたり、計算/公式ミスをすると 雪崩のように失点する
- 特にセンター数学で、誘導に乗れず時間をかけてしまい数IIBの時間切れを招く
等々の理由からこの範囲を苦手とする人が非常に多いです。
このページを読んで下さっているあなたも心当たりがあるのではないでしょうか?
そこでこの連載では、
・三角関数/三角比の公式の覚え方、
・覚えないといけない暗記量を減らすコツ、
・万が一テスト中に忘れてしまっても、すぐ導出できる方法
を特集しています。(ページの最後に連載の総まとめページに戻るリンクを貼ってあります。是非ご覧下さい!)
この範囲で他の受験生と差をつけると、合格ををグッと近づけることが出来ます。
三角関数/三角比の還元公式とは
sin(90°+θ)、sin(π-θ)、cos(1/2π+θ)
など、サイン・コサイン・タンジェントに◯◯度や××ラジアン足したり引いたりした時、どの様な関数に変化するかをまとめたものです。
例:sin(θ+90°)=cosθ やtan(-θ)=-tan(θ)
の様なものです。この還元公式は別名余角の公式・負角の公式・補角の公式などと呼ばれており、主だった物だけでも18種類以上もあります。
上の例の様なものを正確に全て覚えるのは時間のムダな上試験中忘れたら、終了!です。何より三角比・三角関数が嫌いになります。
還元公式を丸暗記せずに行う2step
ここから、上記の余角・負角・補角の公式を覚える代わりに行う方法を紹介します。
[step1] θに±する角度/ラジアンをチェック
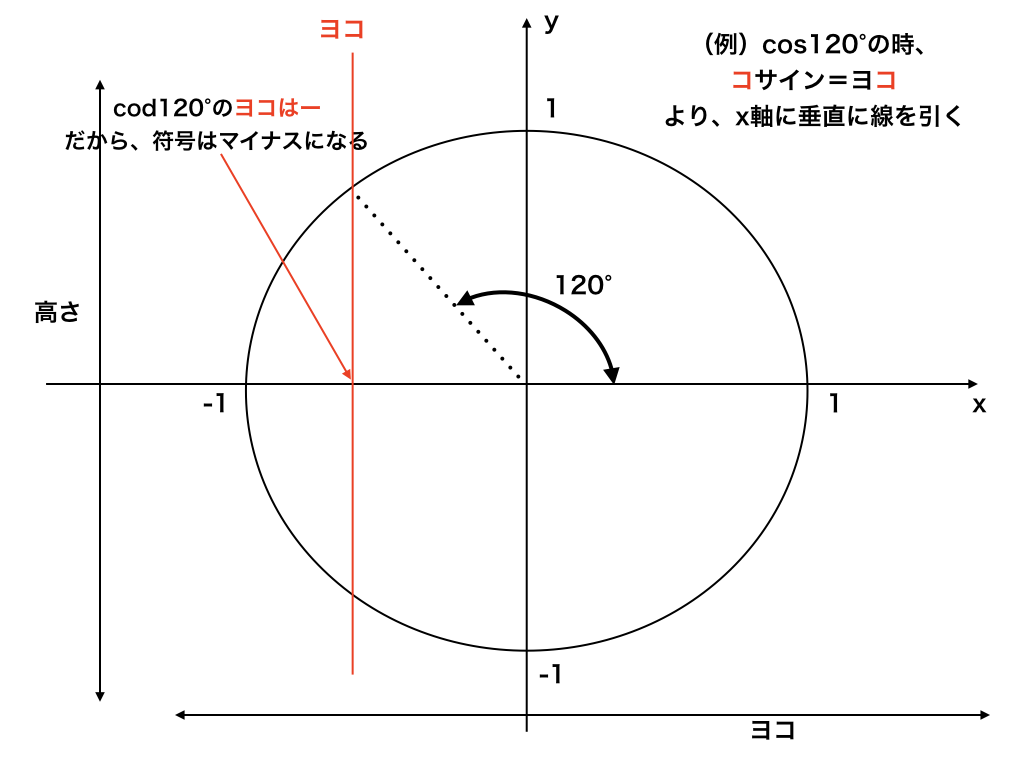
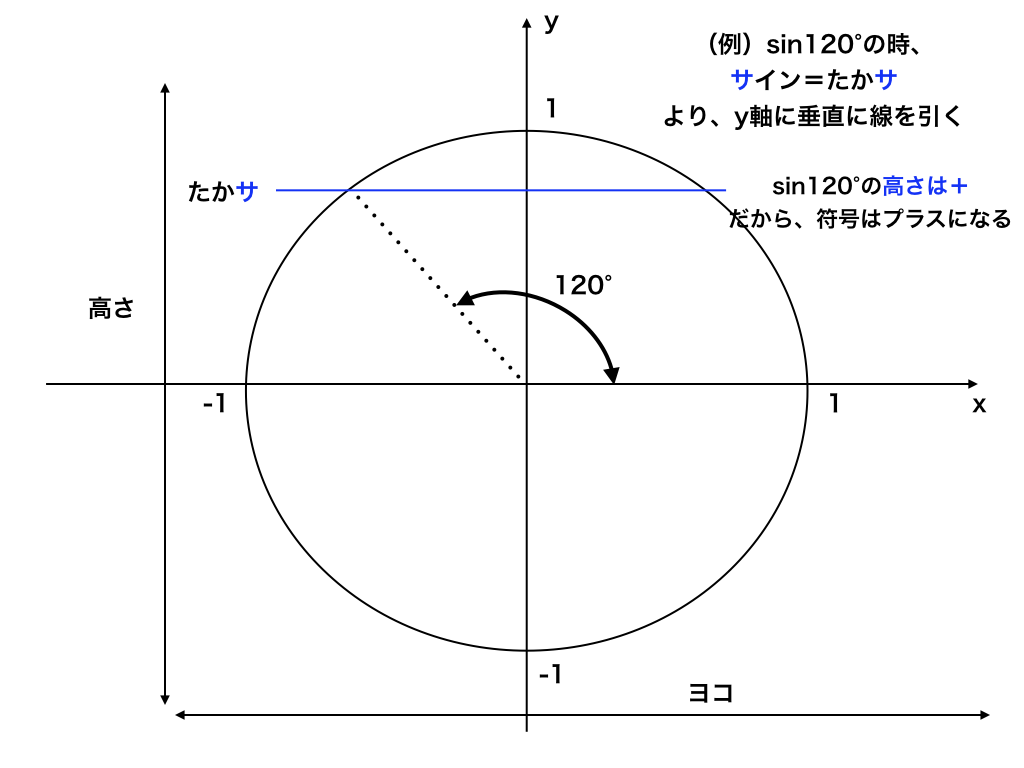
(1)90°、270°(或いはπ/2、3π/2)の時、sinはcosに、cosはsinに、tanは1/tanに関数が変化する。
(2)θに±する角度/ラジアンが0°、180°(或いはπ)の時、sinはsin、cosはcos、tanはtanのままで、関数は変化しない。
[step2]関数が変化する/しないをstep1で確認し、θに90°以下の鋭角を代入してみる。その時の符号とstep1をあわせて答えとする。
この2stepで、かなりの暗記量とミスが削減できます。


還元公式のもう一つの攻略法(加法定理利用型)
以上で還元公式を楽に解く方法(これを解法1とします)を紹介しましたが、
加法定理を使う方法(解法2とします)も有るので、紹介しておきます。
加法定理に付いての証明記事は↓
加法定理の応用記事は↓
さて、例えば
sin(x +π/2)を加法定理を使って解く手順は以下の通りです。
$$sinの加法定理:\sin \left( \alpha \pm \beta \right) =\sin \alpha \cos \beta \pm \cos \alpha \sin \beta $$
$$より、sin\left( x+\frac {\pi }{2}\right) =\sin xcos\frac {\pi }{2}+\cos x\sin \frac {\pi }{2}$$
$$ここで、\cos \frac {\pi }{2}=0,\sin \frac {\pi }{2}=1 なので、$$
$$=sinx・(0) + cosx・(1)$$
$$= cosx$$
という風に簡単に求める事ができます。
解法1を選ぶか、解法2を選ぶかは好みなので、自分が使いやすい方法を選んで下さい。
ただ、どちらの解法を使うにせよ、この記事を見るだけでなく何度か実際に紙に書いて計算し、慣れておいて下さい。