三角関数を含む不等式の解き方と単位円を使うコツ

三角関数が入った不等式の解き方まとめ

「三角方程式の問題を解く方法と関連公式」の続編として、

等式＝の代わりに、≧不等号が入った三角関数の不等式の解き方をまとめています。

三角関数を含む不等式とは

上述したように、三角方程式の不等式バージョンと考えてもらって構いません。

三角方程式は、θの値を求めればよかったのに対して、

不等式ではθの範囲を問われるので少しだけレベルアップします。

単位円を使って不等式を解く

三角関数を含む不等式では、三角方程式と同様に、

θを満たす単位円上に線を引いて値を求め、

角度の条件に気をつけながら《△π＜θ＜○π 》のような形で解答します。

ここでは実際に例題を見ながら解き方を身につけましょう。

三角関数の不等式の例題と解き方

以下の三角関数で表された不等式を解いて、条件を満たすθの値の範囲を求めよ。

ただし、0≦θ＜２πとする。

（例題１）sinθが1/2以上の値をとるとき

（例題２）cosθが1/2以上の値をとるとき

（例題３）2cos²θー3sinθ-3≧０のとき

（例題４）cos2θ≦ーsinθ   のとき

（例題５）sinθ +√3cosθ≧０ をのとき

単位円と三角比・三角関数の復習

三角不等式を解く際も、いろいろな三角比・三角関数の公式や相互関係を利用するので

「三角比・三角関数の公式の導出法と覚え方まとめ」を適宜利用してください。

三角不等式では、三角方程式よりもさらに単位円の重要性が増してきます。

sinθ＝y

cosθ＝x

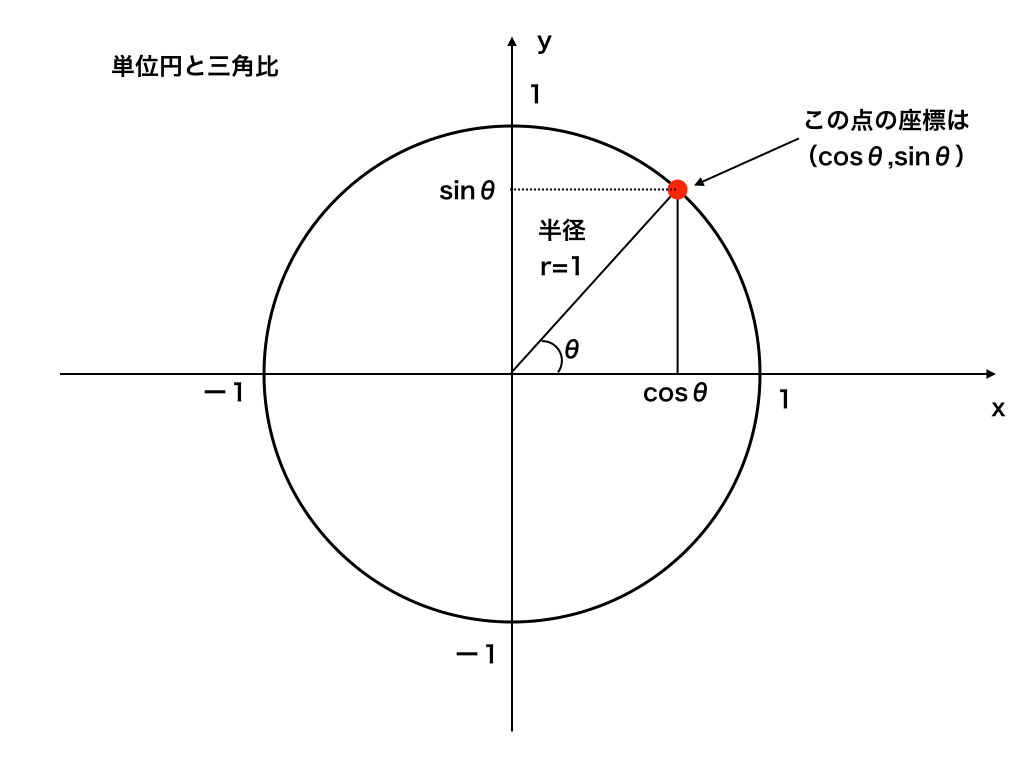
＜単位円とsinθ・cosθ＞

解答解説

解答１：sinと不等式

（解答１）問１はsinθ≧1/2の時のθを求めるので、

単位円とy＝1/2の交点をしらべると、θ＝π/6、5π/6。

sinθは1/2以上なので、図１で青く塗った部分が問１で問われている範囲です。

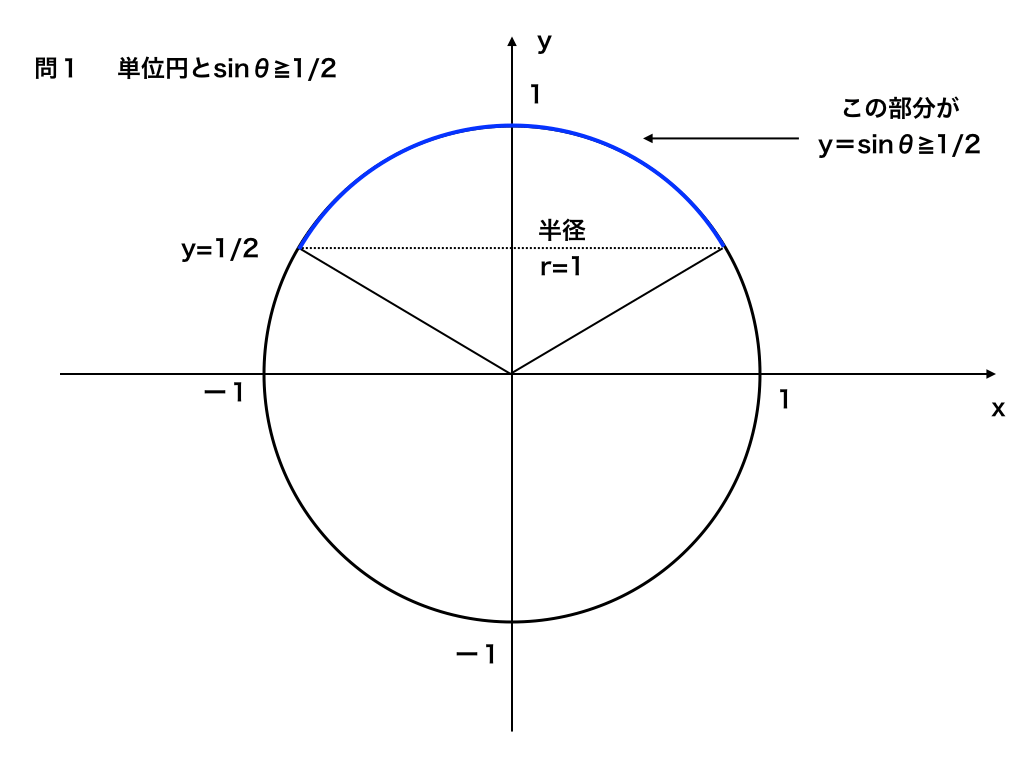
＜問１の単位円＞

したがって、π/6≦θ≦5π/6・・・（答）

解答２：cosと不等式

（解答2）次に、cosθ≧1/2も同様に単位円を書いて同じく調べると

、x＝1/2との交点θ＝π/3、5π/3です。不等号が付いているので、

x≧1/2のところが求めるθの範囲です。

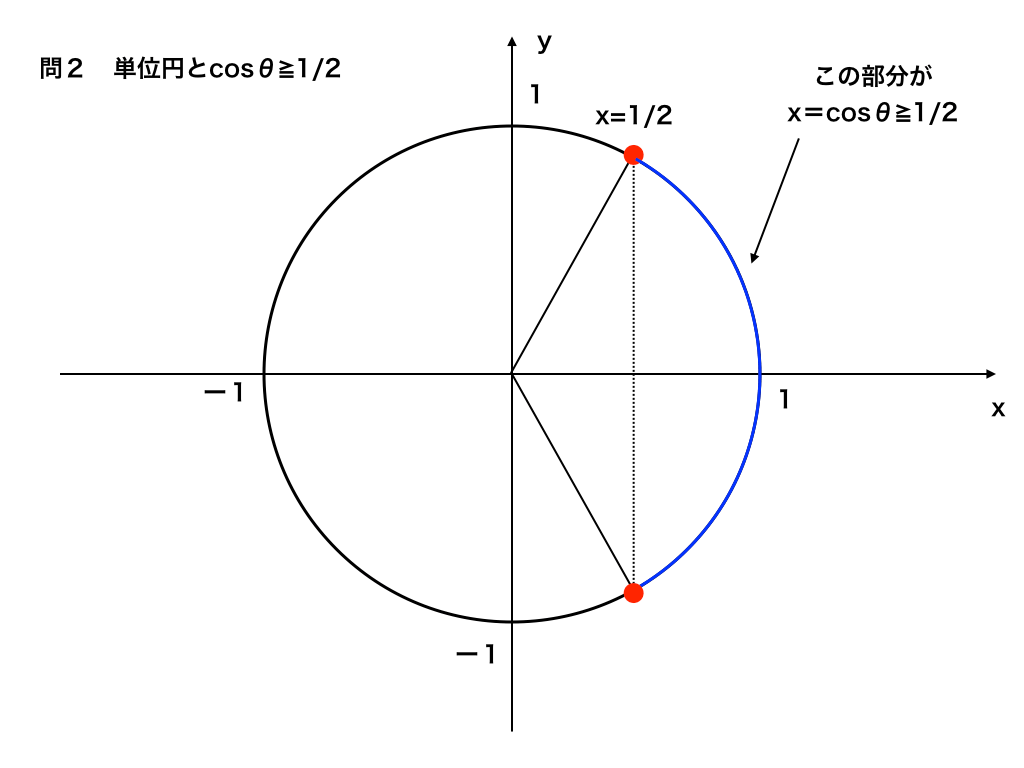
＜問２の単位円＞

ここで、注意が必要な点は、はじめに条件としてθの範囲が決められている（０≦θ＜２π）ので、

”5π/3≦θ≦7π/3”と答えてしまうとバツになります。

そこで、解答は、『0≦θ≦π/3』,『5π/3≦θ＜2π』・・・（答）のように、分けて書くようにします。

解答３：相互関係&因数分解の利用

（解説3）条件の不等式は、2cos²θ-3sinθ-3≧０より、

sin²θ+cos²θ＝１（相互関係）を使って次数の低いsinθに合わせます。

その後、たすき掛けをして＜参考：「因数分解の解き方と工夫まとめ」＞不等式を解いていきます。

2cos²θ-3sinθ-3≧０⇔(2-2sin2θ)-3sinθ-3≧０

不等号の向きに注意して、2sin²θ+3sinθ+1≦０因数分解をすると、

(2sinθ+1)(sinθ+1)≦０

よってsinθの範囲が、-1≦sinθ≦-1/2 と求まります。あとは以下の図よりθの範囲は、

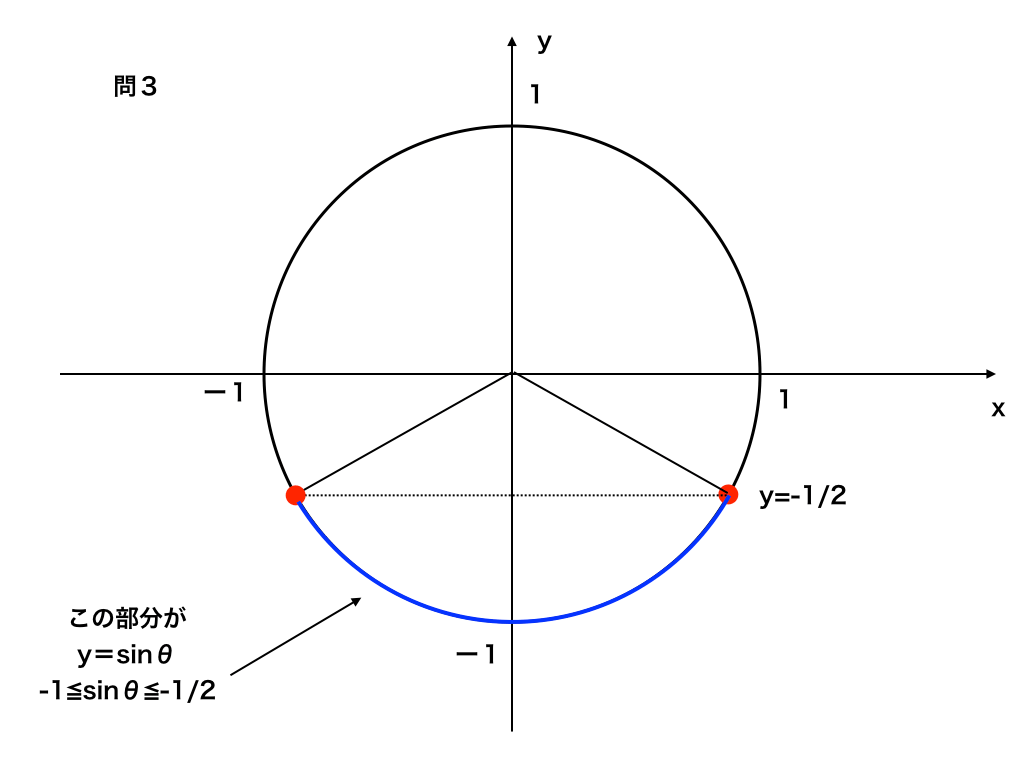
＜問３の単位円＞

7π/6≦θ≦11π/6・・・（答）

解答４：2倍角の公式の利用

（解答4）cos2θ≦-sinθ

ここでは、関数がサインとコサインでそろっておらず、

また角度も、θと2θが混ざってしまっているので、cosの２倍角の定理を用いて式変形をしていきます。

sinθに合わせるため、３種類あるcosの二倍角のうち『cos2θ＝1ー2sin²θ』を使っていきます。

＜参考：「2倍角・３倍角・半角の公式の導き方」＞

１ー2sin²θ＋sinθ≦０　移項して、

2sin²θーsinθ−１≧０　因数分解すると、(２sinθ＋１)(sinθー1)≧０

より、sinθは、１≦sinθ、-π/2≧sinθとなります。

ここで、sinθは−１から１までの値しかとれないので、１＝sinθ,-π/2≧sinθ≧１。

以下の図より、

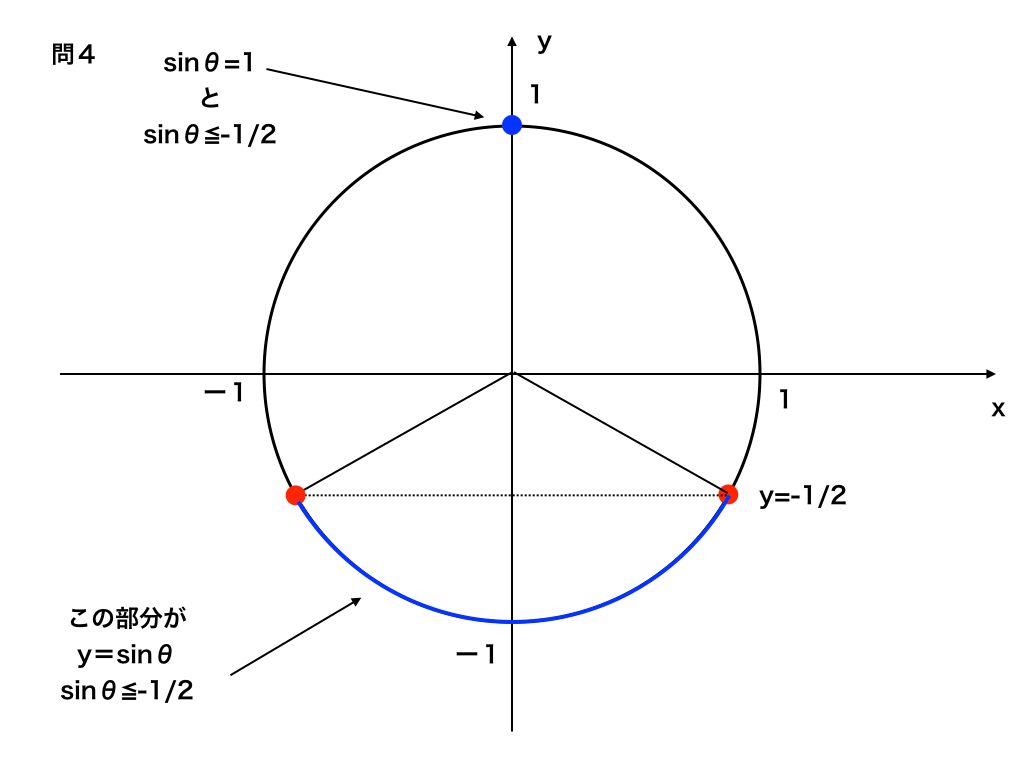
＜問４の単位円＞

θ＝π/2、7π/6≦θ≦11π/6・・・（答）

解答５：合成の利用

（解説5）この不等式も関数がそろっていません。

また、相互関係や倍角公式が使えないので、合成を使います。→「三角関数の合成の正体」

sinθ＋√３cosθ＝２sin(θ+π/3)

2sin(θ+π/3)≧０　両辺を２で割って、sin(θ＋π/3)≧０。

今回は、θが（θ＋π/3）になっているので、０≦(θ+π/3)≦π。

単位円を参考にしながら、問題文の条件（０≦θ<２π）より、０≦θ≦2/3 π または5π/3≦θ<2π・・・（答）となります。

三角方程式・不等式のまとめと三角関数の関連記事

・このように、三角関数を含む不等式（や方程式）では、相互関係や公式、因数分解などあらゆる知識を使ってsinやcosの範囲を決定し、単位円を利用してθを求めます。

・今回のパターン以外にも半角・３倍角・和積/積和の公式を利用するものなど、

たくさんの種類があるのでぜひ多くの類題を解いて、素早く解けるようにしましょう。

＜要チェック！→「三角比/三角関数の公式一覧まとめ」＞

＜方程式と不等式シリーズ＞

以下の記事は、三角関数以外の方程式の解き方をまとめています。ぜひ参考にしてください。

＞＞「高校数学での方程式/不等式の解法総まとめ」＜＜

「2次関数と方程式の解」

「指数/対数方程式の解き方」

「たった２通りの積分方程式の解き方」

「微分方程式の解き方まとめ」

今回も最後までごらんいただき有難うございました。

当サイト「スマホで学ぶサイト、スマナビング！」への記事リクエストやご質問・ご意見はコメント欄にお寄せください。

また、snsでいいね！やシェア、Twitterのフォローをしていただけると助かります。

 ・その他のお問い合わせ/ご依頼に付きましては、お問い合わせページよりお願い致します。