行列の割り算と逆行列
今回は、線形代数学入門の第三回として、行列の割り算を普通の数と対応させて紹介していきます。
その過程で、「逆行列」や「行列式」、「正則行列」などを解説します。
・このシリーズは、行列(線形代数)を0から大学での本格的な線形代数学への橋渡しをするものです。
以前の記事を読んでいない方は、先に
・「線形代数学入門(1):線形代数とは?そして行列の足し算/引き算」
をご覧頂くと理解しやすいです。
・新たに「掃き出し法」を利用して逆行列を求める方法を追加しました。
目次(タップした所へ飛びます)
行列の割り算と逆行列
さて、いきなり結論から言うと、行列にはいわゆる「割り算」は存在しません。
しかしながら、その代わりに「逆行列」と呼ばれるものが存在します。
実数と行列を対応して考える
以下の<図1>の様に、数と行列、逆数と逆行列、1と単位行列Eがそれぞれ対応しているのです。(詳しく説明します。)
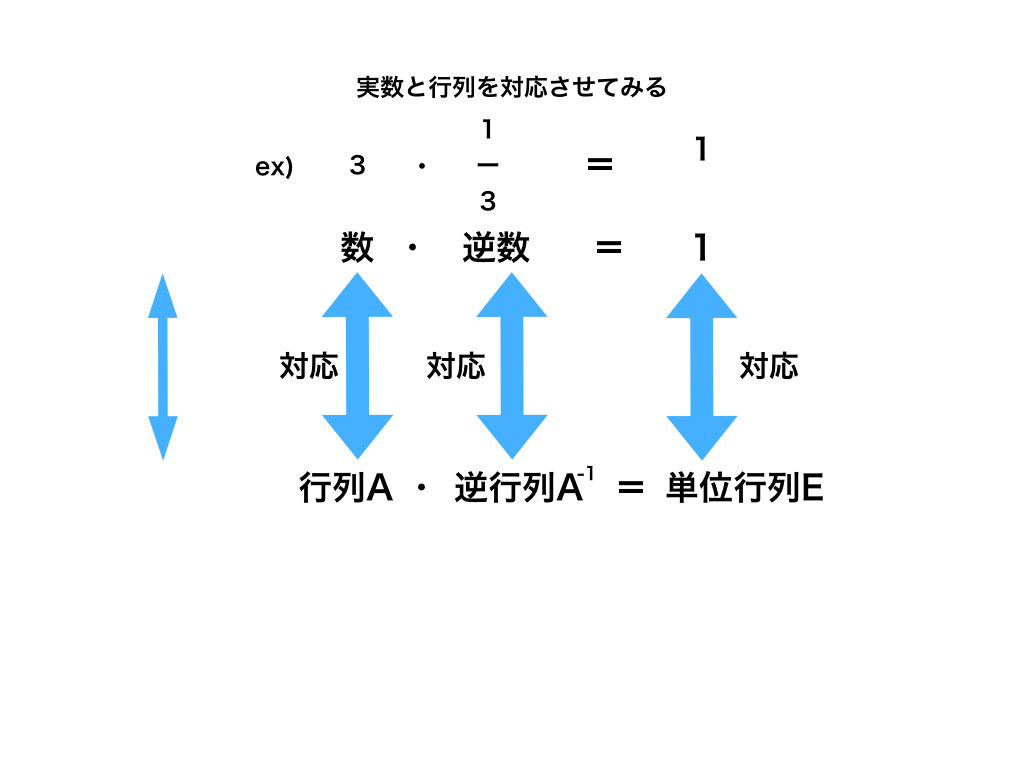
<図1:実数と行列の対応関係>
例えば、実数を7で割ることと、
7の逆数である"1/7"を掛けることは同じ事です。
それと同様の考え方をすれば、「行列を割り算したい」→「その行列の逆行列を掛ければ良い」となります。
逆行列の求め方(1)と求まらない場合
では、その逆行列は常に求まるのでしょうか?また、どのようにして逆行列を計算するのかここから解説していきます。
逆行列は存在しない事もある
結論が先になりますが、逆行列は常に存在するわけではありません。
実数の時を思い出してみると、例えば0の逆数を考えてみます。逆数「1/0」(分母が0)は存在しませんね?。
逆行列と行列式
ここでは2× 2 の2行2列の行列Aの逆行列を求める式を紹介します。
$$行列A=\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}$$
とする時、
$$逆行列A^{-1}=\frac {1}{ad-bc}\begin{pmatrix}
d & -b \\
-c & a
\end{pmatrix}$$
で計算できます。
$$この時\frac{1}{ad-bc}の部分が\frac{1}{0}になる$$
ならば、逆行列は存在しません。(先述した0の逆数が存在しないことと同様です)
行列式とその表記法
この、"1/ad-bc"の分母の部分である“ad-bc”には名前が付いており、「行列式」と呼ばれます。
つまり、行列式:ad-bc=0ならば逆行列は存在せず、
ad-bc≠0ならば逆行列A ^{-1}は存在することになります。
行列式は2×2に限らず、3×3、・・・と存在し、
線形代数において非常に大切なものなので、詳細については別の記事で詳しく取り上げます。
今はとりあえず名前と計算式だけ理解しておいてください。
<線形代数(8)「3×3の行列式を求める”サラスの公式”」の解説記事をアップしました>
正則行列と特異行列
また、逆行列が存在する正方行列(行数と列数が同じ行列詳しくは≫「行列同士の掛け算の順序」)のことを「正則行列」と言います。
一方で、上記のように行列式ad-bcが0である=逆行列が存在しない正方行列のことは「特異行列」と呼ばれます。
逆行列を使って未知の行列を求める。
それぞれ2×2の正方行列A、B、Cについて、AB=Cが成立しており、かつAとCの成分が分かっている時に、行列Bを求める方法を考えてみます。
実数の場合は、再掲する以下の図2のように逆数を両辺にかける事で求めることができました。

<図2:実数と行列の対応(再掲)>
行列も同様に考えて、AB=Cの両辺にAの逆行列を掛けてあげることで
$$A^{-1}AB=CA^{-1}⇔EB=CA^{-1}と計算出来ます。$$
未知の行列を求めてみる
実際に問題を通して解法の流れを習得しましょう。
$$\begin{bmatrix}
3 & 5 \\
1 & 2
\end{bmatrix}B=\begin{bmatrix}
4 & 5 \\
2 & 1
\end{bmatrix}の時、2× 2 の行列Bを求めよ$$
手順1:左辺のBに掛かっている行列をAとして、その逆行列を求める。
$$\begin{bmatrix}
3 & 5 \\
1 & 2
\end{bmatrix}を行列Aとして、その逆行列A^{-1}を求める。$$
(Aとしているのは便宜上です)
A-1は、上記の「逆行列の求め方」より、
$$A^{-1}=\frac {1}{3× 2-5× 1}\begin{bmatrix}
2 & -5 \\
-1 & 3
\end{bmatrix}$$
$$よって、A^{-1}=\begin{bmatrix}
2 & -5 \\
-1 & 3
\end{bmatrix}$$
手順2:両辺にA^{-1}を順番に注意して掛ける
(左辺)はA-1ABと左側からかけているので、(右辺)も左から掛ける。
$$(左辺)=\begin{bmatrix}
2 & -5 \\
-1 & 3
\end{bmatrix}\begin{bmatrix}
3 & 5 \\
1 & 2
\end{bmatrix}B$$
$$(右辺)=\begin{bmatrix}
2 & -5 \\
-1 & 3
\end{bmatrix}\begin{bmatrix}
4 & 5 \\
2 & 1
\end{bmatrix}$$
手順3:AA^{-1}=Eと「単位行列の特徴」を利用する。
単位行列の特徴の一つである、「どんな行列との積も、掛けた行列になる」ことを利用します。
(これは、実数の世界で、「1」をどんな数と掛け合わせても、掛け合わせた数になることと同様です。)
1× 5=5 のように、E *A=A となる。
$$\begin{bmatrix}
2 & -5 \\
-1 & 3
\end{bmatrix}\begin{bmatrix}
3 & 5 \\
1 & 2
\end{bmatrix}=$$
$$\begin{bmatrix}
2・ 3+\left( -5\right) ・ 1 & 2・ 5+\left( -5\right) ・ 2 \\
\left( -1\right) ・ 3+3・ 1 & \left( -1\right) ・ 5+3・2
\end{bmatrix}$$
$$=\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}と確かに単位行列になっています。$$
$$EB=\begin{pmatrix}
2 & -5 \\
-1 & 3
\end{pmatrix}\begin{pmatrix}
4 & 5 \\
2 & 1
\end{pmatrix}$$
$$B=\begin{pmatrix}
2・ 4+\left( -5\right) ・ 2 & 2・ 5+\left( -5\right) ・ 1 \\
-1・ 4+3・ 2 & \left( -1\right) ・ 5+3・ 1
\end{pmatrix}$$
を計算すると、
$$行列B=\begin{pmatrix}
-2 & 5 \\
2 & -2
\end{pmatrix}と求まります。$$
手順4:検算をしてみる。
本当にBが正しいのか、検算をしてみましょう。
$$(左辺)=\begin{pmatrix}
3 & 5 \\
1 & 2
\end{pmatrix}\begin{pmatrix}
-2 & 5 \\
2 & -2
\end{pmatrix}$$
$$=\begin{pmatrix}
3・ \left( -2\right) +5・ 2 & 3・ 5+5・ \left( -2\right) \\
1・ \left( -2\right) +2・ 2 & 1・ 5+2・ \left( -2\right)
\end{pmatrix}$$
$$=\begin{pmatrix}
4 & 5 \\
2 & 1
\end{pmatrix}$$
元の式の右辺の行列と同じになったので、確かに計算が正しいことがわかりました。
・・・ここから逆行列の作り方(2)に入ります。・・・
<ここからの内容>:逆行列の作り方その2:掃き出し法(ガウスの消去法)の利用(線形代数第8回・第9回で学ぶ知識を利用するので、必要に応じて以下のリンクからご覧ください。)
掃き出し法を用いて連立方程式を解いた第8回:「掃き出し法と連立方程式の解」と、第9回:「非正則行列に掃き出し法を用いて階段行列を作る」を利用して『逆行列を作る方法』を紹介します。
<これまでの線形代数学の入門記事>:「0からわかる線形代数の解説記事一覧」
逆行列を掃き出し法で求める
ここでは、上述した通り『掃き出し法』の要領で逆行列を求めますが、先ほどの逆行列の作り方(1)と何が違うのか、少し触れておきます。
上の方法(1)で紹介した方法は、2×2サイズの行列のみにしか適用できませんでした。
が、掃き出し法を使用した今回の方法を使うと、正則であれば、3×3・4×4・・・とサイズが大きくなっても逆行列を求めることができます。
拡大係数行列と掃き出し法(ガウスの消去法)による逆行列の作り方(手順)
手順は非常に単純なので、第8回・第9回の掃き出し法をマスターしていれば普通の計算を繰り返すだけで逆行列を作ることが可能です。
ここでは例として、$$A=\begin{pmatrix}
2 & 3 & 3 \\
1 & 2 & 5 \\
-1 & -1 & 3
\end{pmatrix}$$
の3×3行列の逆行列を求めながら手順を1つ1つ確認していきます。
手順0:先に行列式を求めて正則行列か確かめておく
まずサラスの公式より行列式を求めます。
$$\det A=12-15-3-(-6)-(-10)-9=1$$
よって、行列式≠0なのでAは正則行列であることが確認できました・
手順1:拡大係数行列を作る
次に、(A|E)の形をした『拡大係数行列』を作成します。
$$\begin{pmatrix}
2 & 3 & 3 & 1 & 0 & 0 \\
1 & 2 & 5 & 0 & 1 & 0 \\
-1 & -1 & 3 & 0 & 0 & 1
\end{pmatrix}$$
行列の左3列がA,右3列が単位行列Eになっていることが確認できます。
手順2:元の行列の部分を単位行列Eにする(行基本操作)
ここから、行基本操作を繰り返して、行列の左3列の部分がEになるように変形していきます。
・まず1行目と2行目を入れ替えて、1列目の2行・3行の部分を0にします。{(2行目)ー2×(1行目)と、(2行目)+(3行目)を計算する)}
すると、次のようになります。
$$\begin{pmatrix}
1 & 2 & 5 & 0 & 1 & 0 \\
0 & -1 & -7 & 1 & -2 & 0 \\
0 & 1 & 8 & 0 & 1 & 1
\end{pmatrix}$$
・さらに、2行目と3行目を入れ替えて、2列目は2行2列の成分のみ0になるように計算します。
{(1行目)ー2×(2行目)、と、(2行目)+(3行目)を計算}
$$\begin{pmatrix}
1 & 0 & -11 & 0 & -1 & -2 \\
0 & 1 & 8 & 0 & 1 & 1 \\
0 & 0 & 1 & 1 & -1 & 1
\end{pmatrix}$$
・最後に、3列目の1行・2行目の成分を0にするために、{(1行目)+11×(3行目)、と、(2行目)ー8×(3行目)を行います。}
$$\begin{pmatrix}
1 & 0 & 0 & 11 & -12 & 9 \\
0 & 1 & 0 & -8 & 9 & -7 \\
0 & 0 & 1 & 1 & -1 & 1
\end{pmatrix}$$
・・・これで左半分が単位行列Eになりました。
手順3:拡大係数行列の右半分が元の行列の逆行列
この拡大係数行列の右側3列の部分
$$\begin{pmatrix}
11 & -12 & 9 \\
-8 & 9 & -7 \\
1 & -1 & 1
\end{pmatrix}$$がAの逆行列になっています。
実際に検算してみましょう。
検算してみる:AA-1=E
「行列どうしのかけ算の仕方」の通りに
$$\begin{pmatrix}
2 & 3 & 3 \\
1 & 2 & 5 \\
-1 & -1 & 3
\end{pmatrix}\begin{pmatrix}
11 & -12 & 9 \\
-8 & 9 & -7 \\
1 & -1 & 1
\end{pmatrix}$$
を計算すると、確かに単位行例Eになることから、逆行列であることが確かめられました。
逆行列のまとめと3つ目の方法
・逆行列は、元の行列と掛け合わせて単位行列Eになるもの
・逆行列が常に存在するわけではなく、行列式=0の時は存在しない
・3×3以上のサイズの逆行列を求める際には『掃き出し法』を使う
・次回は、今回までの知識を使って「一次変換」と言われる分野を初めから見ていきます。
《NEW》逆行列の三番目の求め方である「余因子行列」を用いた方法についての記事を作成しました。→「余因子行列の作り方と逆行列の公式への応用」
線形代数学入門シリーズ一覧
>>「【随時更新】線形代数シリーズ:0から学べる記事総まとめ【保存版】」を読む<<
・第一回:「線形代数入門1:行列の意味と演算」
・第二回:「線形代数入門2:行列同士の積」
・第三回:「今ココです」
・第四回:「一次変換とは?意味と仕組みを解説」
・第五回:「固有値と固有ベクトルの求め方&その意味」
・第六回:「対角化/対角行列の意味と手順をわかりやすく解説!行列のn乗への応用も」
今回も最後までご覧いただき本当に有難うございました。
当サイト「スマナビング!」では読者の方のご意見や、記事のリクエストなどをもとに改善・記事の追加、更新を行なっています。
・記事のリクエストとご質問・ご意見はコメント欄にお寄せください。
・また、多くの方に利用して頂くため、にSNSでシェア・当サイト公式Twitterのフォローをして頂くと大変励みになります。
・より良い記事作成と「スマホ一台でいつでも、どこでも、必要な人へ学びを提供する」為にぜひご協力お願い致します!
・その他のお問い合わせ/ご依頼等はお問い合わせページよりお願い致します。

