
行列の固有値と固有ベクトルの意味と求め方
<今回の内容>:前回「線形代数入門(4):一次変換の意味と実践」に引き続き、今回は「行列の固有値」と「固有ベクトル」の意味と求め方について詳しく解説していきます。記事の終盤には対角化を解説した記事へのリンクを用意しているので、スムーズに『対角化・対角行列』の理解が進みます。
(これまでの線形代数入門シリーズは、以下のリンクよりご覧頂けます。)
>>「【随時更新】線形代数シリーズ:0から学べる記事総まとめ【保存版】」を読む<<
行列の固有値と固有ベクトルの意味と計算の仕方
固有値(λで表されるスカラー)、固有ベクトルは、のちに学ぶ「対角化」やそれを応用した行列のべき乗をはじめ、線形代数学に必須です。
この記事では、最も単純な2行2列の実行列のλと固有ベクトルを求めていきます。
固有値λ・固有ベクトルAの定義と求める目的
正方行列Aと、零ベクトルでないベクトル(x,y)、そしてスカラー「λ」の間に
$$A\begin{pmatrix}
x \\
y
\end{pmatrix}=λ\begin{pmatrix}
x \\
y
\end{pmatrix}$$
が成立する時、ベクトル
$$\begin{pmatrix}
x \\
y
\end{pmatrix}$$
を「固有ベクトル」、スカラーλを「固有値」といいます。
これだけでは、何をしているのかわからないと思うので、実際に例を使って解説していきます。
ちなみに、この固有値と固有ベクトルを求める目的は、主に「対角化」と呼ばれる正方行列を「対角行列」にするときに固有値・固有ベクトルが必要になるためです。
(対角化と対角行列については次回の「線形代数(6)対角化と行列のべき乗」で詳しく説明しています。)
固有値・固有ベクトルと一次変換(本題:図解)
さらに『固有』には重要な意味があります。
普通、行列を使ってベクトルの一次(線形)変換を行うと、(一次変換については→「一次変換とは何か?を解説」)そのベクトルは回転したり、拡大・縮小します。つまり全く異なるベクトルになるわけです。
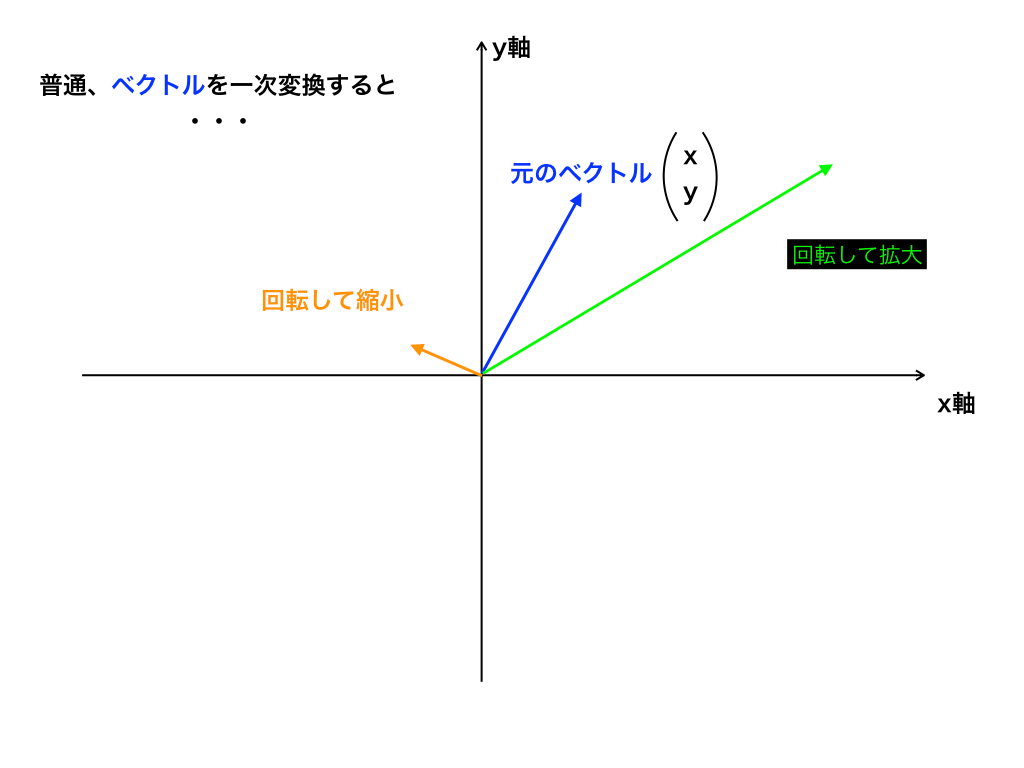
<一次変換されたベクトル図>
ところが、そのベクトルが“固有ベクトル”の場合には「向きの変化=回転」が起こらず、大きさ=すなわちベクトルの長さ“だけ”が変化するのです。
そして、一次変換をする前と後の”固有ベクトルの長さの比“こそが「固有値λ」なのです。
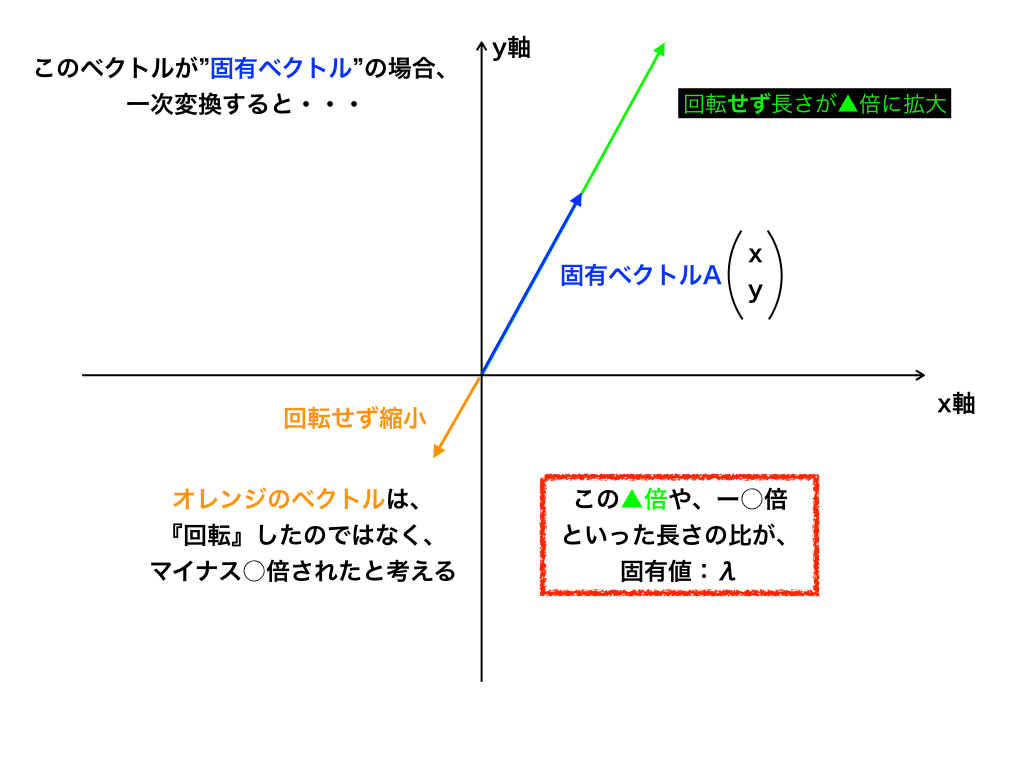
<固有ベクトルを一時変換した場合>
・・・なんとなく”固有“という言葉が付いている理由が分かったでしょうか?
これらの性質を応用し、現代ではAI:人工知能の分野で固有値・固有ベクトルは大活躍しています。
(線形代数と機械学習(人工知能のなかの一分野)には切っても切れない関係があります。興味のある方はぜひ→「機械学習シリーズ一覧」を読んでみてください!)
固有値問題(λを求める手順)
さて、固有値の意味に触れたところで実際にλを求めてみましょう。
一般化した解き方では分かりにくいので、この記事では、2行2列の行列
$$B=\begin{bmatrix}
4 & 1 \\
6 & 5
\end{bmatrix}$$の固有値λと固有ベクトル$$A=\begin{pmatrix}
x \\
y
\end{pmatrix}$$
を実際に求める手順を確認します。
定義より、以下の式を満たすAとλを求めていきます。
$$\begin{bmatrix}
4 & 1 \\
6 & 5
\end{bmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}=λ \begin{pmatrix}
x \\
y
\end{pmatrix}…(※)$$
第一段階:単位行列Eを右辺にかける
単位行列$$E=\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}$$は、「逆行列と行列同士の割り算」の記事でも解説しましたが、実数における『1』と同じように扱えます。
そこで、(※)の式の右辺にEをかけます。
$$(右辺)=\begin{aligned}=λ \begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}\\
=\begin{bmatrix}
λ & 0 \\
0 & λ
\end{bmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}\end{aligned}$$
途中の計算式がわからない方は→「行列の計算(スカラー倍・和・差)」を再確認してください。
第二段階:移項して固有ベクトルでくくる
次に、右辺を左辺に移項した上で、固有ベクトルでくくります。
$$\left( \begin{bmatrix}
4 & 1 \\
6 & 5
\end{bmatrix}-\begin{bmatrix}
λ & 0 \\
0 & λ
\end{bmatrix}\right) \begin{pmatrix}
x \\
y
\end{pmatrix}=0$$
行列の部分を足して、整理すると
$$\begin{bmatrix}
4-λ & 1 \\
6 & 5-λ
\end{bmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}=0$$
第三段階:行列式から固有方程式を作る
行列部分を仮にLとおきます。このLは逆行列を持ちません。
したがって、Lの行列式:det L=0。<参考:「逆行列と行列式~行列の割り算は存在するか?~」>
これを利用して、Lの行列式から、λの方程式(固有方程式と呼びます。)を作ります。
$$\det L=( 4-λ) ( 5-λ) -( 1×6)$$
第四段階:固有方程式を解いて固有値を2つ求める
$$\det L=λ ^{2}-9λ +14=(λ-7)(λ-2) $$
よって、固有値λ=2、または7であることがわかりました。
固有ベクトルを求める
固有値が求まれば、あとは式に代入していきます。
定義の式(※)より、
$$\begin{bmatrix}
4-λ & 1 \\
6 & 5-λ
\end{bmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}=0$$
(1)λ=2の時
$$\begin{bmatrix}
2 & 1 \\
6 & 3
\end{bmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}=0$$
(2)λ=7の時
$$\begin{bmatrix}
-3 & 1 \\
6 & -2
\end{bmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}=0$$
行列と固有ベクトルを掛けて式を作る
λ=2のとき
(2x+y)+(6x+3y)=0
8x+4y=0・・・(1)
λ=7のとき
(-3x+y)+(6x-2y)=0
3x-y=0・・・(2)
x、yを満たす数を選ぶ
ここで、上2つの式の(x、y)を満たす数を選びます。
この際、選ぶ数の組は無数にあるので、なるべく簡単なものを選びましょう。
今回は、(1)を満たす(x、y)=(1、-2)、(2)を満たす(x、y)=(-1、-3)とします。
・・・・・・
この記事の頭のほうで、固有ベクトルは一次変換しても向きが変化しないベクトルであることを紹介しました。
ここでは具体的なベクトル(xyの組み)を選びました。(分野は異なりますが、、)整数の不定方程式(→「一次不定方程式の一般解の求め方」)で一般解を表したように、適当な文字を使うことで、λに対するあらゆる固有ベクトルを表すことができます。(現在作成中)
固有値と固有ベクトルをまとめる
かなり長かったですが、これで固有値λと固有ベクトルAが求まりました。
$$行列B=\begin{bmatrix}
4 & 1 \\
6 & 5
\end{bmatrix}$$
$$固有値λ=2のとき、固有ベクトル(の一つ)は\begin{pmatrix}
1 \\
-2
\end{pmatrix}$$
$$固有値λ=7のとき、固有ベクトル(の一つ)は\begin{pmatrix}
-1 \\
-3
\end{pmatrix}$$
固有値・固有ベクトルを一般化しよう
ここからは、2×2以上の3×3行列の固有値/固有ベクトルをはじめ、n×n行列の固有方程式を一般化していきます。
また(xy)で表していたベクトルをxとし、Aをn行n列の正方行列とします。
Ax=λx
一般化した固有方程式と固有(特性)多項式
を移項し、xベクトルで括ります。
この際、(A-λE)x=0・・・(※)
ここで、単位行列Eに注意して下さい。
これは、Eは掛けても行列は変化しないことを利用して、先に右辺にEを掛けておき、Ax=λEx の形にしてから、移項すると(※)の形になります。
さらに(※)の(A-λE)を行列式にします。
$$A=\begin{vmatrix}
a_{1,1}, & \ldots & a_{n,1} \\
\vdots & \ddots & \vdots \\
a_{1,n} & \ldots & a_{n,n}
\end{vmatrix}$$
$$単位行列E=\begin{vmatrix}
1, & \ldots & 0 \\
\vdots & \ddots & \vdots \\
0 & \ldots & 1
\end{vmatrix}$$
とλを使ってそれぞれの行列式の成分を計算すると、
行列Aー(λ・単位行列E)より
$$|A-\lambda E|=\begin{vmatrix}
a_{1,1}-\lambda, & \ldots & a_{1,n} \\
\vdots & \ddots & \vdots \\
a_{n,1} & \ldots & a_{n,n}-\lambda
\end{vmatrix}$$
対角成分(=行番号と列番号が同じ)場所のみ$$a_{i,i}-\lambda, (i=1,2,\ldots,n)$$
の行列式の形になります(これを特性(固有)多項式と呼び、$$\varphi _{A}\left( x\right)$$ で表します。
更に、以下のように固有多項式と0を=で結んだ式を特性(固有)方程式と呼びます。
$$\begin{vmatrix}
a_{1,1}-\lambda, & \ldots & a_{1,n} \\
\vdots & \ddots & \vdots \\
a_{n,1} & \ldots & a_{n,n}-\lambda
\end{vmatrix}=0$$
3次の行列の固有値/ベクトルを求める
上で、n次の固有方程式についてあつかったので、今度は3×3行列での固有値・固有ベクトルについて取り組んでみましょう。
なお、ここからは「行・列それぞれの基本操作」を利用して固有値を求めていくので、未習の方は先に、→(「掃き出し法による連立方程式の解き方の『行・列基本操作の部分』」)をご覧ください。
例題:次の行列Aの固有値と固有ベクトルを求めよ。
$$行列A=\begin{pmatrix}
2 & 1 & 1 \\
0 & 1 & 0 \\
0 & 3 & 1
\end{pmatrix}$$
の固有値と固有ベクトルを求めます。
固有(特性)多項式:
$$|A-λE|=\varphi _{A}\left( x\right) =\begin{vmatrix}
2-\lambda & 1 & 1 \\
0 & 1-\lambda & 0 \\
0 & 3 & 1-\lambda
\end{vmatrix}=0$$
この固有方程式を解くと、
$$(1-λ)^{2}(2-λ)=0,よって、λ=1,2$$
ここで、固有値λ=1の時、
λ=1を代入して、
$$\begin{pmatrix}
1 & 1 & 1 \\
0 & 0 & 0 \\
0 & 3 & 0
\end{pmatrix}$$
これを行基本変形していきます。
1行目-(2行目×1/3)と、2行目×1/3より
$$\begin{pmatrix}
1 & 0 & 1 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{pmatrix}$$
$$ここで、\begin{pmatrix}
1 & 0 & 1 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{pmatrix}\begin{bmatrix}
x \\
y \\
z
\end{bmatrix}=\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}$$
より、この行列のランクは2,自由度は:3−2=1であることがわかります。
(rank・自由度については「階段行列の作り方とランク・自由度とは?」で詳しく解説しています)
よって、x=-z、かつ、y=0だから、x=kとおくと
$$\begin{bmatrix}
k \\
0 \\
-k
\end{bmatrix}=k\begin{bmatrix}
1 \\
0 \\
-1
\end{bmatrix}$$
固有値λ=2の時
$$\begin{pmatrix}
0 & 1 & 1 \\
0 & -1 & 0 \\
0 & 3 & -1
\end{pmatrix}$$
これも行基本操作をおこなって、
3行目ー(1行目×3)
$$\begin{pmatrix}
0 & 1 & 1 \\
0 & 0 & 1 \\
0 & 0 & -4
\end{pmatrix}$$
2行目×4+3行目、と、1行目ー2行目より
$$\begin{pmatrix}
0 & 1 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{pmatrix}\begin{bmatrix}
x \\
y \\
z
\end{bmatrix}=\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}$$
この行列もrank=2、自由度は3−2=1
したがって、z、y=0、x=tとおくと
$$\begin{pmatrix}
t \\
0 \\
0
\end{pmatrix}=t\begin{bmatrix}
1 \\
0 \\
0
\end{bmatrix}$$
まとめ
以上をまとめて、行列Aの固有値と固有ベクトルは
固有値λ=1(重解)のとき、固有ベクトル$$k\begin{bmatrix}
1 \\
0 \\
-1
\end{bmatrix}$$(kは任意の実数)
固有値λ=2のとき、固有ベクトル$$t\begin{bmatrix}
1 \\
0 \\
-1
\end{bmatrix}$$(tは任意の実数)
が答えです。
固有値/固有ベクトルのまとめ対角化の解説記事へ
今回は2×2の行列のλ、Aについて求めたうえで、固有多項式を一般化し、3×3サイズの行列の固有値・固有ベクトルを求めるところまで解説しました。
途中で行基本変形やランク・自由度などが登場してボリュームが多かったかと思うので、よく復習しておいてください!
次回は、この記事で学んだ固有値・固有ベクトルを使って行列を「対角行列」にする「対角化」と、対角化をさらに応用して”行列のn乗を求める方法”を解説します。
→対角化・対角行列とn乗を作成しました。以下のリンク(第6回)より続けてご覧ください。
「対角化/対角行列の意味と手順をわかりやすく解説!行列のn乗への応用も」
線形代数(行列)入門シリーズ一覧
>>「【随時更新】線形代数シリーズ:0から学べる記事総まとめ【保存版】」を読む<<
第0回:「集合と写像をわかりやすく:線形代数への道しるべ」
第1回:「線形代数の意味と行列の足し算・引き算・スカラー倍」
第2回:「行列どうしの掛け算の手順をわかりやすく!」
第3回:「逆行列と行列の割り算、正則行列について」
第4回:「一次変換(線形変換)とは?」
第5回:「今ここです」
第6回;「対角化/対角行列の意味と手順をわかりやすく解説!行列のn乗への応用も」
(NEW)
第7回:「連立方程式を行列を使って解く手順(1)」
最後までご覧いただき、誠にありがとうございました。
このサイトは皆さんのご意見や、記事のリクエストなどをもとに日々改善、記事の追加・更新を行なっています。
そこで
・記事のリクエストや、ご質問・ご意見はコメント欄にお寄せください。
・多くの方に利用し、知っていただくためにSNSでのシェア(拡散)&スマホで学ぶサイト、スマナビング!公式Twitterのフォローをして頂くと励みになります!
・より良いサイト運営のためにご協力お願い致します。

