線形代数入門シリーズ(8)3元一次連立方程式
<第八回の内容>3×3行列の行列式の求め方(サラスの公式)から掃き出し法(ガウスの消去法)による3元一次連立方程式の解き方まで。
<必要な予備知識>「線形代数(7)2元一次連立方程式を解く」・
(「線形代数入門0から解説記事まとめ」)
目次(タップした所へ飛びます)
掃き出し法で連立方程式を解く
前回は、2×2の行列と行列式を用いて2元1次連立方程式の解を求める方法を紹介しました。今回は、その3×3行列(3元一次連立方程式)バージョンです。
難易度はぐっとアップしますが、3×3の今回の方法をマスターすれば、それ以上のサイズでも対応できるようになるので、ぜひじっくり取り組みましょう。
まず、掃き出し法を利用する前の準備として、正則行列かどうかの確認をするための行列式を求める方法(=サラスの公式)を紹介します。
サラスの公式(行列式の求め方)
2×2の行列式の場合と比べて(参考:「2×2行列の逆行列と行列式の求め方」)、計算量・手順ともにかなり煩雑になりますが、何度か手を動かして解いていくうちに慣れてくるので安心してください。
手順1:成分を斜め(右下)に掛け合わせる
まず、図のように行列の成分をかけていきます。対角成分(a,e,i)はわかりやすいですが、残りの2つは少しややこしいです。
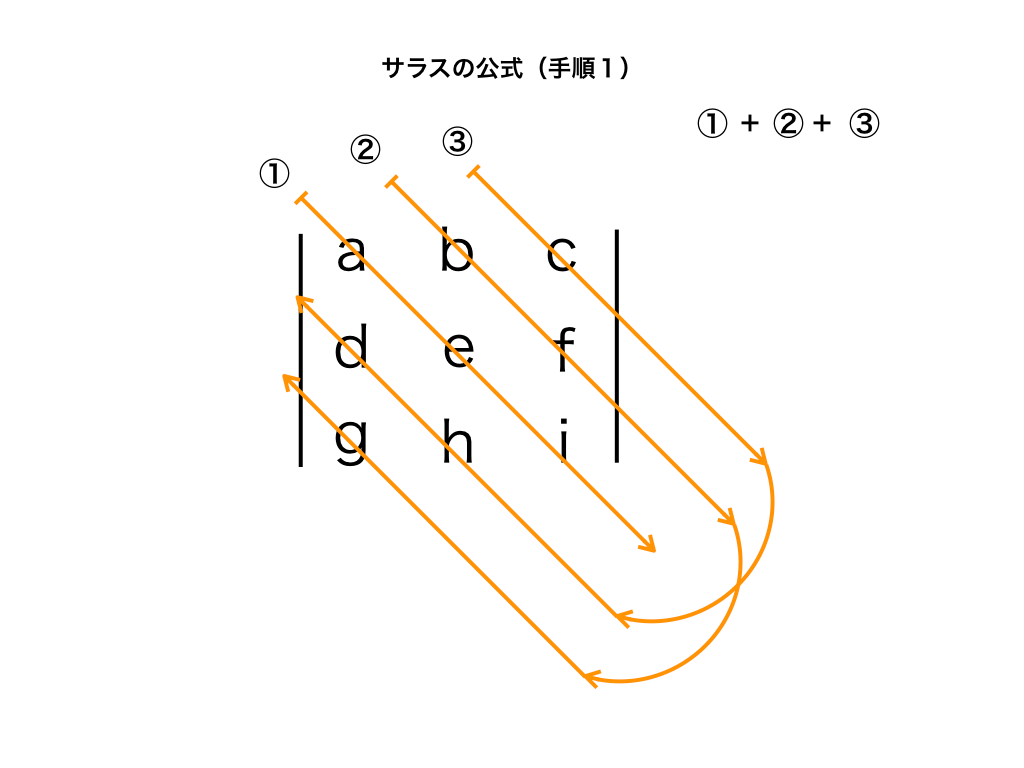
具体的には、『aei +bfg +chd 』という計算を行います。オレンジの線の矢印の方向へ掛け合わせていきます。
手順2:成分を斜め(左下)に掛け合わせる
次に、手順1と同様の掛け算を以下の図のとおりに行います。
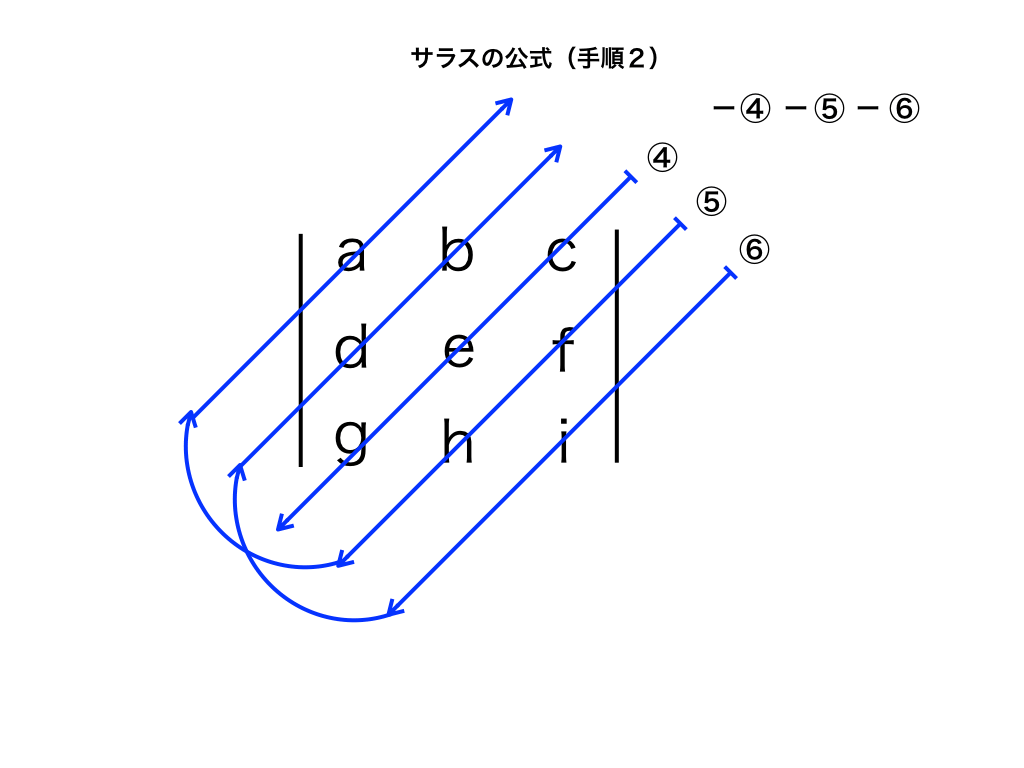
−ceg−fha−idb
ただし、符号がマイナスになっている点に注意が必要です。
手順3:(1の和)ー(2の和)を計算する=行列式
最後に、(1)と(2)の結果を合わせて計算を行います。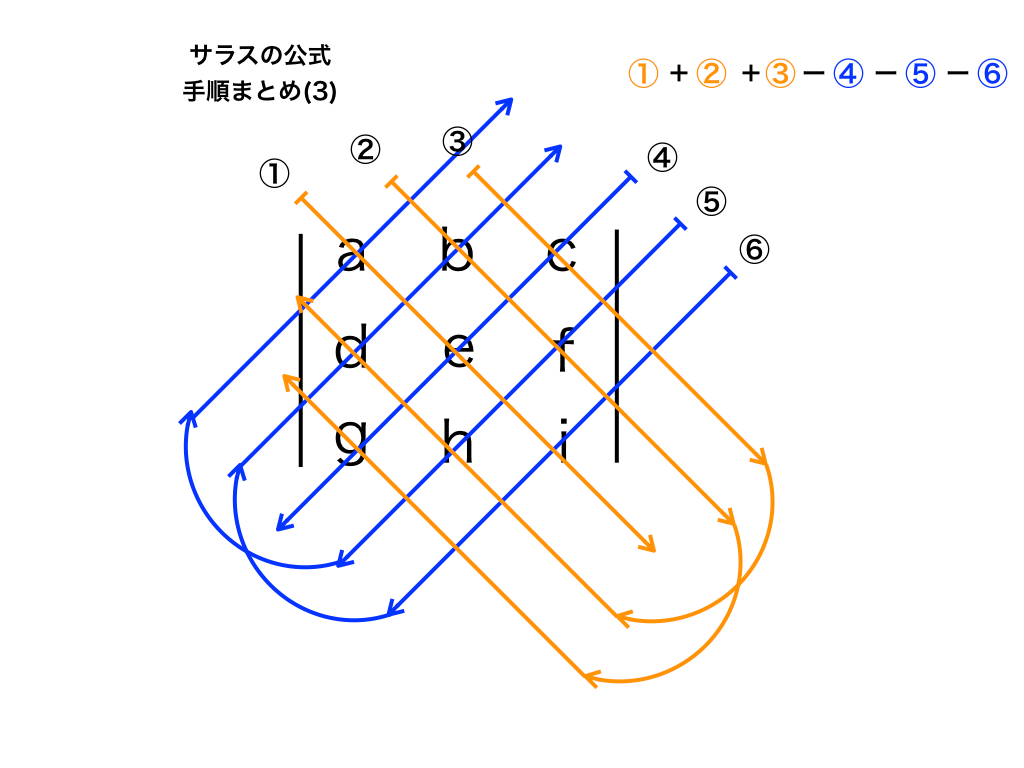
<3×3の行列式を求める>
まとめると、この行列の行列式:
$$\det A=|A|=aei +bfg +chd−ceg−fha−idb$$と求まります。
掃き出し法による3元1次連立方程式の解き方の手順
準備が整ったところで、いよいよ3元一次連立方程式の解き方に入ります。
今回は次の3元一次連立方程式を例として解説していきます。
2x+y+3z=6
x+3y+2z=1
3x-2y-z=7
正則行列であるか行列式を求めて確かめる
前回:二元一次連立方程式(「連立方程式を行列で解く方法(8)」)のときと同様に、まず行列の積の形であらわします。
$$\begin{bmatrix}
2 & 1 & 3 \\
1 & 3 & 2 \\
3 & -2 & -1
\end{bmatrix}\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}=\begin{pmatrix}
6 \\
1 \\
7
\end{pmatrix}$$
次にこの行列の行列式を上で学んだ「サラスの公式」を使って計算します。
$$\det A=|A|=-24$$
したがって、行列式≠0。
・行列式|A|=0、すなわち逆行列が存在せず正則行列でない場合については、次回(「階段行列とrank、自由度の意味と求め方」で詳しく解説します。)
この例題では、行列式|A|≠0で、正則行列であることがわかったので、解を求める方法を見ていきましょう。
行基本操作の手順とコツ
何をしているのか初めはわかりにくいですが、とりあえず「単位行列E」の形にすることを目標に、”対角成分を1に、それ以外の成分を0にする”ということを頭に入れながら以下の操作をみてみてください。
行基本操作とは
・行を別の行と入れ替える
・ある行を○倍する
・他の行に○倍した行を足す/引く
これらの操作を何度も繰り返すことを「行基本操作」と言います。
掃き出し法で実際に連立方程式を解く
では、先ほど例示した連立方程式を行列の積の形にし、さらに以下のように(行列|解)の形を作ります。(この行列を『拡大(係数)行列』と呼びます。)
$$\begin{pmatrix}
2 & 1 & 3 & 6 \\
1 & 3 & 2 & 1 \\
3 & -2 & -1 & 7
\end{pmatrix}$$
そして、『拡大(係数)行列』を行基本操作によって、(単位行列|●)の形に変形した時の●が連立方程式の解になります。
$$\begin{pmatrix}
1 & & & xの解 \\
& 1 & & yの解 \\
& & 1 & zの解
\end{pmatrix}$$
具体的に見ていきましょう。
1列目の1行目の成分だけ1になるよう変形する
まず、2行目と1行目を入れ替えて、左上の成分が1になるようにします。
$$\begin{pmatrix}
1 & 3 & 2 & 1 \\
2 & 1 & 3 & 6 \\
3 & -2 & -1 & 7
\end{pmatrix}$$
次に、単位行列にするためには1列目の2と3が不要なので、この二つを0にする→『2行目ー(入れ替えた1行目×2)』を行い、3行目についても同様に、『3行目ー(1行目×3)』という計算をします。
$$\begin{pmatrix}
1 & 3 & 2 & 1 \\
0 & -5 & -1 & 4 \\
0 & -11 & -7 & 4
\end{pmatrix}$$
2列目の2行目だけ1にする
今度は、2列目の2行の成分だけを1にするように、操作を繰り返します。
2行目と3行目を入れ替えて、2行目を(-1/11)倍すると2行2列の成分が『1』になります。
$$\begin{pmatrix}
1 & 3 & 2 & 1 \\
0 & 1 & \frac{7}{11} & \frac{-4}{11} \\
0 & -5 & -1 & 4
\end{pmatrix}$$
次に、『1行目ー2行目×3』と『3行目+2行目×5』の操作を行うことで、1行2列と3行2列目の成分が0になります。(分数が多くなるので計算ミスに気をつけましょう。)
$$\begin{pmatrix}
1 & 0 & \frac{1}{11} & \frac{23}{11} \\
0 & 1 & \frac{7}{11} & \frac{-4}{11} \\
0 & 0 & \frac{24}{11} & \frac{24}{11}
\end{pmatrix}$$
3列目の3行目だけ1にする
残りは、3列目だけです。これまでと同じく単位行列Eにすることを目標に操作していきます。
3行目を(11/24)倍することによって、3行3列目の成分が1になり、後は1行3列と2行3列の成分を0にすれば行基本操作は終了です。
$$\begin{bmatrix}
1 & 0 & \frac{1}{11} & \frac{23}{11} \\
0 & 1 & \frac{7}{11} & \frac{-4}{11} \\
0 & 0 & 1 & 1
\end{bmatrix}$$
この行列の『1行目ー3行目×1/11』と『2行目ー3行目×7/11』を計算すると
$$\begin{bmatrix}
1 & 0 & 0 & 2 \\
0 & 1 & 0 & -1 \\
0 & 0 & 1 & 1
\end{bmatrix}$$
となって、第1列目〜3列目までが単位行列となり、初めの目標の形にすることができました。
$$したがって、\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}=\begin{pmatrix}
2 \\
-1 \\
1
\end{pmatrix}$$
さて、途中に分数の計算が出てきてかなり大変でしたが、単位行列の右側の解(x y,z)を元々の三つの方程式に代入すると正しいことが確認できるかと思います。
このようにして連立方程式の解を求める方法を『掃き出し法』(あるいは『ガウスの消去法』)と呼びます。
(我々人間はこの『掃き出し法』のような、”単純な操作を繰り返していくこと”は不得手ですが、コンピューターは何の苦もなく高速・かつ正確に行うことができます。このような理由もあり、コンピューターの仕組み・機械学習の理論の理解には線形代数の知識が必須となるのです。)
掃き出し法で逆行列を求める
掃き出し法は、このように連立方程式を解くためだけではなく、「逆行列」を求める際にも利用する事ができます。
詳しくは、→「逆行列の求め方2種類とそれぞれの意味」をご覧下さい!
掃き出し法(ガウスの消去法)まとめと次回:階段行列とrankへ
・今回は、3×3サイズの行列式を求めるために、『サラスの公式』を紹介しました。
(サラスの公式は3次の行列を対象にしていましたが、n次の行列式を求める方法は→「余因子展開と行列式の求め方」および、「置換・互換と行列式の定義式の意味を理解する」をご覧ください。)
・次に、3元1次連立方程式の解法として、『行基本操作』と『掃き出し法』を解説しました。
・次回は、操作する行列が非正則行列(『行列式=0』)の場合について詳しく説明していきます。
線形代数入門シリーズ一覧
これまでの線形代数の記事は以下のまとめよりご覧いただけます。
・「0からの線形代数入門:解説記事総まとめ」<<
次回:線形代数第9回「階段行列とランク・自由度と正則行列でない場合の連立方程式の解法」
最後までご覧いただき有難うございました。
「スマナビング!」では、読者の皆さんのご意見や、ご質問、記事のリクエストの募集を行なっています。
ぜひ、コメント欄までお寄せください。
・いいね!、B!やシェア、Twitterのフォローをしていただけると励みになります。
・お問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。

