線形代数入門シリーズ(4):一次変換
この「線形代数入門シリーズ」は、高校数学と大学の本格的な線形代数学との隙間を埋めるものです。
今回は、「一次変換」について解説していきます。なお、これまでの第一回〜第三回で紹介した行列の知識は必須なので、未読の方はぜひ以下のリンクから先にお読みください。
(第二回・第三回と関連記事はまとめからもご覧いただけます。)
>>「【随時更新】線形代数シリーズ:0から学べる記事総まとめ【保存版】」を読む<<
目次(タップした所へ飛びます)
一次変換とは何なのか?
はじめに、一次変換(線形変換とも言います)とはどういったものなのかを書いておきます。
厳密な定義は「集合と写像」(←作成しました。一部追記中。)の知識が必要なので、大体の意味が分かれば読み進めて下さい。
変換:「座標上の点を別の点に移す(移動させる)事」(正確には、ある集合から同一の集合への写像を変換という)
座標上の点《(x,y)とします》を、別の座標《(X,Y)とします》に移す時、新しい座標が、X=ax+by の様に「定数項を含まない一次式」で表される時、この移動を一次(線形)変換と言います。
更に、これを行列を使って表すと、
$$\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
ax+by \\
cx+dy
\end{pmatrix}=\begin{pmatrix}
X \\
Y
\end{pmatrix}$$
となり、この時、元の座標に掛けた
$$行列\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}$$
の事を「この一次変換を表す行列」と呼びます。
・・・なかなかややこしいですね。
しかし、このシリーズはあくまで『大学で学ぶ整形代数への橋渡し』がテーマなので、
詳しくは大学で学ぶとして、まずは具体的に一次変換の例を見てみましょう。
座標上の点を一次変換してみる。
実際に行列Aの表す一次変換によって、xy座標上の点(1,2)がどの様に移動するのか見てみます。
$$行列A=\begin{pmatrix}
-1 & 0\\
0 & -1
\end{pmatrix}とします。$$
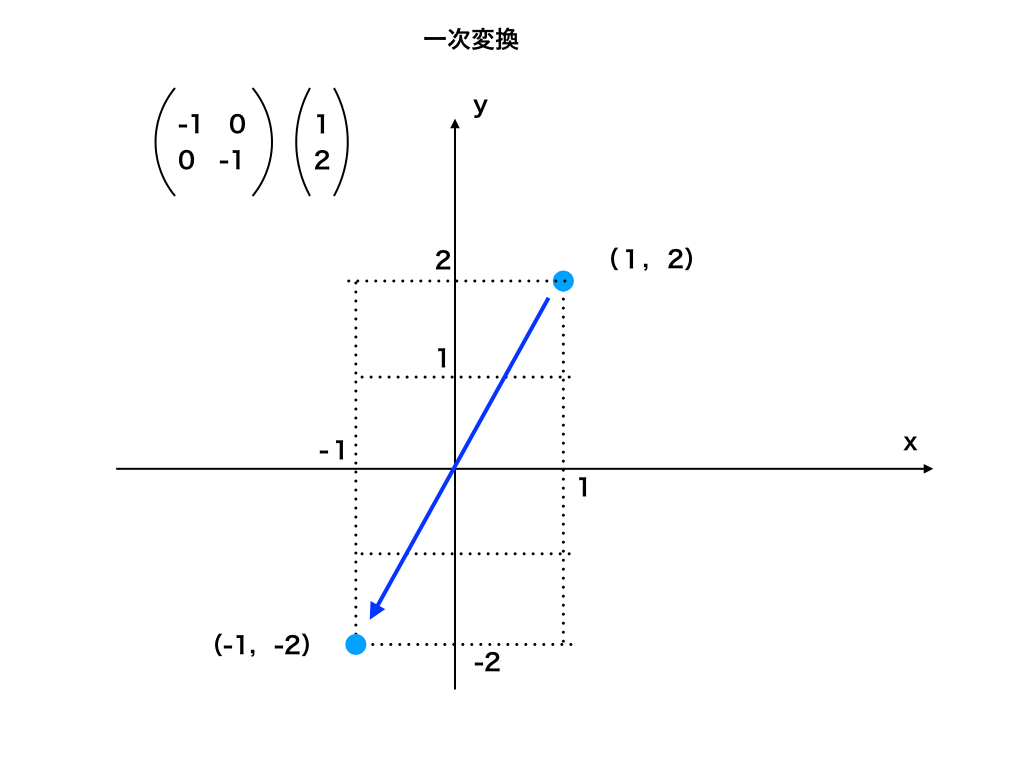
$$すると、\begin{pmatrix}
-1 & 0 \\
0 & -1
\end{pmatrix}\begin{pmatrix}
1 \\
2
\end{pmatrix}=\begin{pmatrix}
-1 \\
-2
\end{pmatrix}$$
となり、点(1,2)は(-1,-2)に移動します。
複数の点を一次変換する
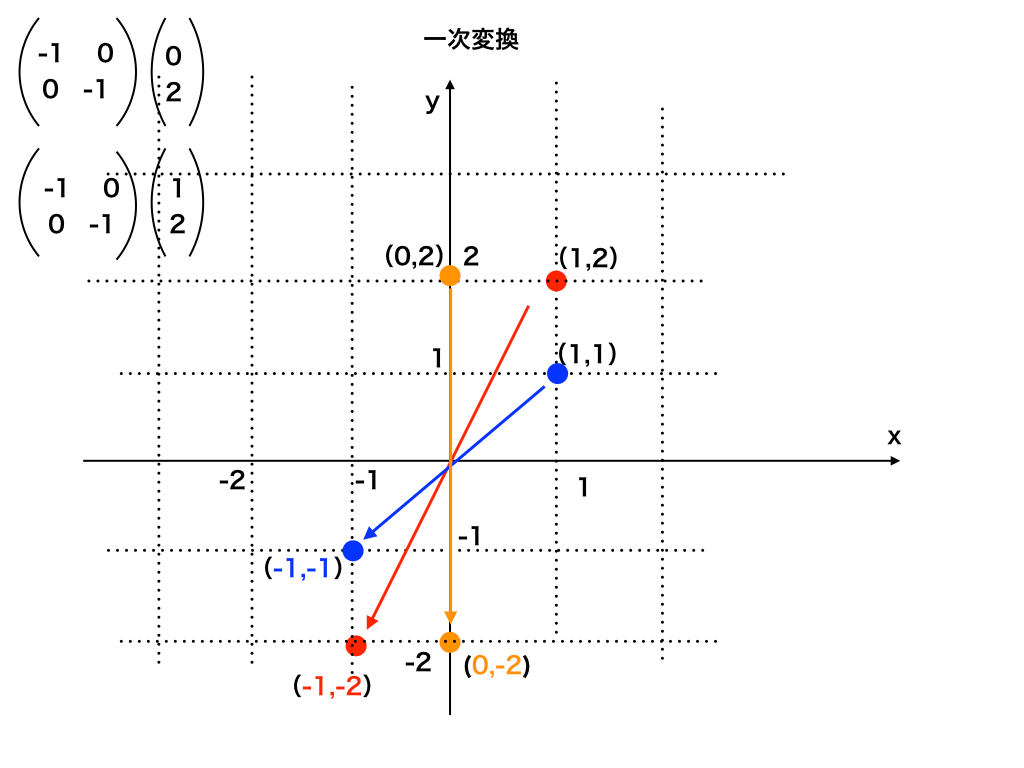
今度は、複数の点に行列Aをかけてみます。

このように、行列Aをかけると「原点に関して、対称に移動している」ことがわかるでしょうか?
複素数平面でも、座標上の点を移動させたり拡大縮小させることがありました。
一次変換も、行列をかけるだけで移動させることができる、大変便利なものなのです。
以下に、x軸やy軸に関して対称に移動させたり、θ回転させたい時に座標に「掛ける」行列を並べておきます。
反時計回りにθ回転させたい時
θ反時計回りに回転させるとき、
$$行列\begin{pmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & cos\theta
\end{pmatrix}$$
x軸に対称に移動させる
$$\begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}$$
y軸に対称に移動させる
$$\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}$$
原点に対称に移動させる
$$\begin{pmatrix}
-1 & 0 \\
0 & -1
\end{pmatrix}$$
先ほども出てきましたよね。
行列式と一次変換の関係
ここからは、「逆行列とは?行列の割り算と行列式」で取り上げた、“行列式”と一次変換について解説していきます。
上で取り上げた例では、掛けた行列Aの行列式が≠0でしたが、
行列式=0である行列とかけ合わせると一体どうなるのでしょうか?
$$行列B=\begin{pmatrix}
1 & 3 \\
2 & 6
\end{pmatrix}$$
として、以下の図のような青色の点(0,1)、赤色の点(1,1)、オレンジ色の点(0,2)にそれぞれBをかけてみると、、
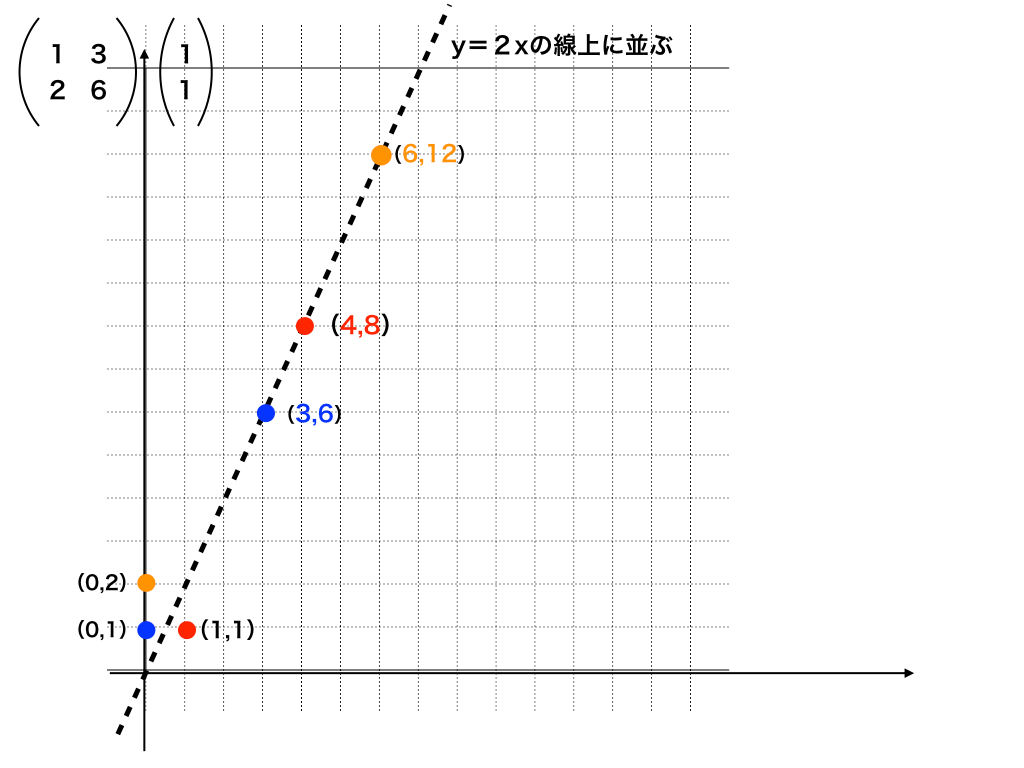
このようにy=2xの一直線上に並んでいます。
このように、行列式と一次変換には
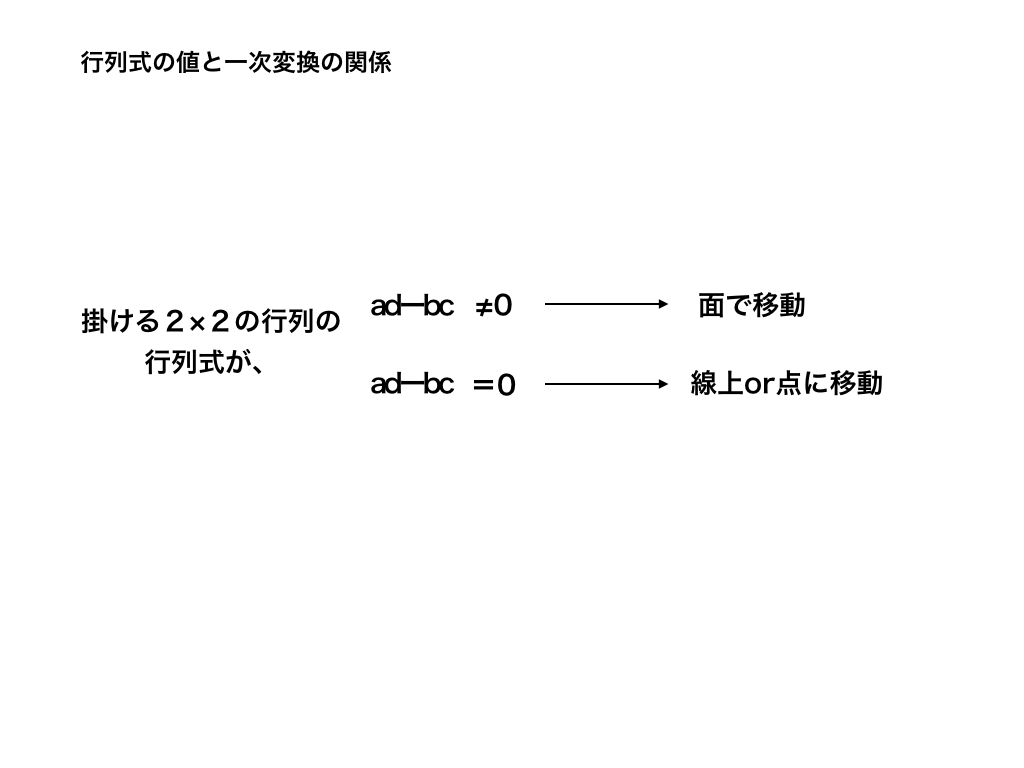
上のような関係があります。
一次変換の練習問題
例題:ある一次変換によって、座標(1,2)が(7,14)に移り、(4,3)は(13,31)に移った。
問:この一次変換を表す2行2列の行列Aを求めよ。
この問題は、これまで紹介してきた一次変換を応用したものです。
少し時間をとって考えてみてください。
解説
とにかくこの一次変換を表す行列が全くわからないので、2×2の行列Aの成分を以下のように仮定します。
$$まず、行列A=\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}とおいて、$$
$$A\begin{pmatrix}
1 \\
2
\end{pmatrix}=\begin{pmatrix}
7 \\
14
\end{pmatrix}$$
$$A\begin{pmatrix}
4 \\
3
\end{pmatrix}=\begin{pmatrix}
13 \\
31
\end{pmatrix}より、$$
$$\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}\begin{pmatrix}
1 \\
2
\end{pmatrix}=\begin{pmatrix}
a+2b \\
c+2d
\end{pmatrix}=\begin{pmatrix}
7 \\
14
\end{pmatrix}$$
$$\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}\begin{pmatrix}
4 \\
3
\end{pmatrix}=\begin{pmatrix}
4a+3b \\
4c+3d
\end{pmatrix}=\begin{pmatrix}
13 \\
31
\end{pmatrix}$$
ここで、a,b,c,dについて解くと、
a+2b=7と、4a+3b=13これを解いて、
a=1,b=3。
c+2d=14と、4c+3d=31を解いて、
同様に、
c=4,d=5。
$$したがって、行列A=\begin{pmatrix}
1 & 3 \\
4 & 5
\end{pmatrix}$$
一次変換のまとめ
・いかがでしたか?定義の部分など難しいところがあったかと思いますが、一次変換がどういったものなのか、何となくでもイメージ出来るようになって貰えれば幸いです。
関連記事と線形代数(行列)入門シリーズ
>>「【随時更新】線形代数シリーズ:0から学べる記事総まとめ【保存版】」を読む<<
第1回:「線形代数の意味と行列の足し算引き算・スカラー倍」
第2回:「行列同士の掛け算の手順をわかりやすく!」
第3回:「逆行列と行列の割り算、正則行列について」
第4回:今ここです
第5回:「固有値と固有ベクトルの計算・求め方をわかりやすく解説」
第6回:「ケーリー・ハミルトンの定理と行列のべき乗(制作中)」
今回も最後までご覧いただき有難うございました。
・記事のリクエストなどは、コメント欄までお寄せください。
・また、多く方に利用して頂くためにSNSでシェア&弊サイト公式Twitterのフォローをして頂くと助かります!
・より良いサイト運営と記事作成の為に是非ご協力お願い致します!
・その他のお問い合わせ/ご依頼等は、お問い合わせページよりお願い致します。

