余因子行列と応用(線形代数第11回)
<この記事の内容>:前回の「余因子の意味と計算と余因子展開の方法」に引き続き、”余因子行列”という新たな行列の意味・作り方と、それを利用して”逆行列”を計算する方法など『具体的な応用法』を解説していきます。
<これまでの記事>:「0から学ぶ線形代数:解説記事総まとめ」からご覧いただけます。
目次(タップした所へ飛びます)
余因子行列とは
はじめに、『余因子行列』とはどういった行列なのかイラストと共に紹介していきます。
各成分が余因子の行列を考える
前回、余因子を求める方法を紹介しましたが、その"余因子を行列の要素とする行列"のことを言います。(そのままですね!)
ここでは例として『$$行列A=\begin{bmatrix}
2 & 1 & 2 \\
3 & 5 & 2 \\
1 & 4 & 1
\end{bmatrix}$$』の3×3行列の余因子を求め、さらに余因子行列を作っていきます。
余因子行列を作る+注意点
行列Aの1行1列目の余因子を$$c_{1,1}、1行2列目をc_{1,2}・・・として並べ$$
>>$$A=\begin{bmatrix}
c_{1,1} & c_{1,2} & c_{1,3} \\
c_{2,1} & c_{2,2} & c_{2,3} \\
c_{3,1} & c_{3,2} & c_{3,3}
\end{bmatrix}$$、それらを『転置』することで$$A^{T}=\tilde{A}=\begin{bmatrix}
c_{1,1} & c_{2,1} & c_{3,1} \\
c_{1,2} & c_{2,2} & c_{3,2} \\
c_{1,3} & c_{2,3} & c_{3,3}
\end{bmatrix}$$
が求まります。(ここでは、$$Aの余因子行列をAの上に〜を付けた\tilde{A}$$とし、$$Aの右上のTは『転置』、A^{T}をAの転置行列とします。$$)
対角成分以外の成分が全て(行,列)→(列,行)になっています。
では、$$A=\begin{pmatrix}
2 & 1 & 2 \\
3 & 5 & 2 \\
1 & 4 & 1
\end{pmatrix}$$の転置前の行列を作り、その後転置して余因子行列を完成させます。
(再掲:「確認用:余因子の求め方」)
$$\begin{bmatrix}
\begin{vmatrix}
5 & 2 \\
4 & 1
\end{vmatrix} &-\begin{vmatrix}
3 & 2 \\
1 & 1
\end{vmatrix} &\begin{vmatrix}
3 & 5 \\
1 & 4
\end{vmatrix} \\
- \begin{vmatrix}
1 & 2 \\
4 & 1
\end{vmatrix} & \begin{vmatrix}
2 & 2 \\
1 & 1
\end{vmatrix} & -\begin{vmatrix}
2 & 1 \\
3 & 4
\end{vmatrix} \\
\begin{vmatrix}
1 & 2 \\
5 & 2
\end{vmatrix} & -\begin{vmatrix}
2 & 2 \\
3 & 2
\end{vmatrix} & \begin{vmatrix}
2 & 1 \\
3 & 5
\end{vmatrix}
\end{bmatrix}$$
行列Aの内部の各成分(2×2の行列式)を計算すると、
$$A=\begin{pmatrix}
-3 & -1 & 7 \\
7 & 0 & -7 \\
-8 & 2 & 7
\end{pmatrix}これを転置すると$$
$$A^{T}=\tilde{A}=\begin{pmatrix}
-3 & 7 & -8 \\
-1 & 0 & 2 \\
7 & -7 & 7
\end{pmatrix}$$
このようにして、余因子行列が求まります。
余因子行列と逆行列の関係式
余因子行列の作り方が分かったところで、次にこれを利用することを考えます。
冒頭でも述べましたが、『逆行列』を余因子行列から作ることができるのです。
その公式と理由を次の項で紹介します。
余因子行列→逆行列の公式
公式:行列式の性質より
$$A\cdot \tilde{A}=\begin{pmatrix}
|A| & 0 & \ldots & 0 \\
0 & |A|& \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & |A|
\end{pmatrix}$$
このように対角成分にのみ”Aの行列式”が並び、その他の成分は全て0となります。
ここで、|A|をくくり出して、$$A\cdot \tilde{A}=|A|\begin{pmatrix}
1 & 0 & \ldots & 0 \\
0 & 1& \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & 1
\end{pmatrix}$$
とすると、単位行列Eができるので、
$$A\cdot \tilde{A}=|A|E$$と変形できます。さらに、行列式が≠0のもとで、両辺を|A|で割ると
$$A\cdot \frac{\tilde{A}}{|A|}=E$$
となります。さらに行列とその逆行列の積は単位行列になることから
$$A\cdot A^{-1}=E$$
上下の式を比較すると、余因子行列,行列式と逆行列を結ぶ公式:
$$\frac{\tilde{A}}{|A|}=A^{-1}$$
を導けます。
逆行列の作り方(2×2・掃き出し法)との違い
これまで(参考:「逆行列の意味と作り方2種類の紹介記事」)解説してきたように、逆行列を求める方法は2×2行列の場合は公式で、それ以上の場合は掃き出し法(ガウスの消去法)を主に使います。
では今回の余因子(行列の公式)を使った方法をいつ使うの?と思われるのではないでしょうか。
基本的には《3×3までのサイズ、かつ余因子が計算しやすい行列の場合》なのですが、この辺りの「どの方法が最も早く正確に計算できるか」は、多少の慣れが必要かもしれません。
実際に手を動かして計算していくと自然と最適な方法が分かる様になるので、類題を探して解いていってみてください!
実際に公式から逆行列を作り出す
実際に、公式を使用して逆行列を作ってみましょう。
ここでは、3×3の行列A=の逆行列を求めます。
余因子行列→逆行列の公式より、
$$A^{-1}=\frac {-A}{\left| A\right| }$$
ここで、先ほどの行列の逆行列を求めると、
$$\frac{1}{|A|}\tilde{A}$$
サラスの公式より|A|=7,参考:「サラスの公式と掃き出し法」
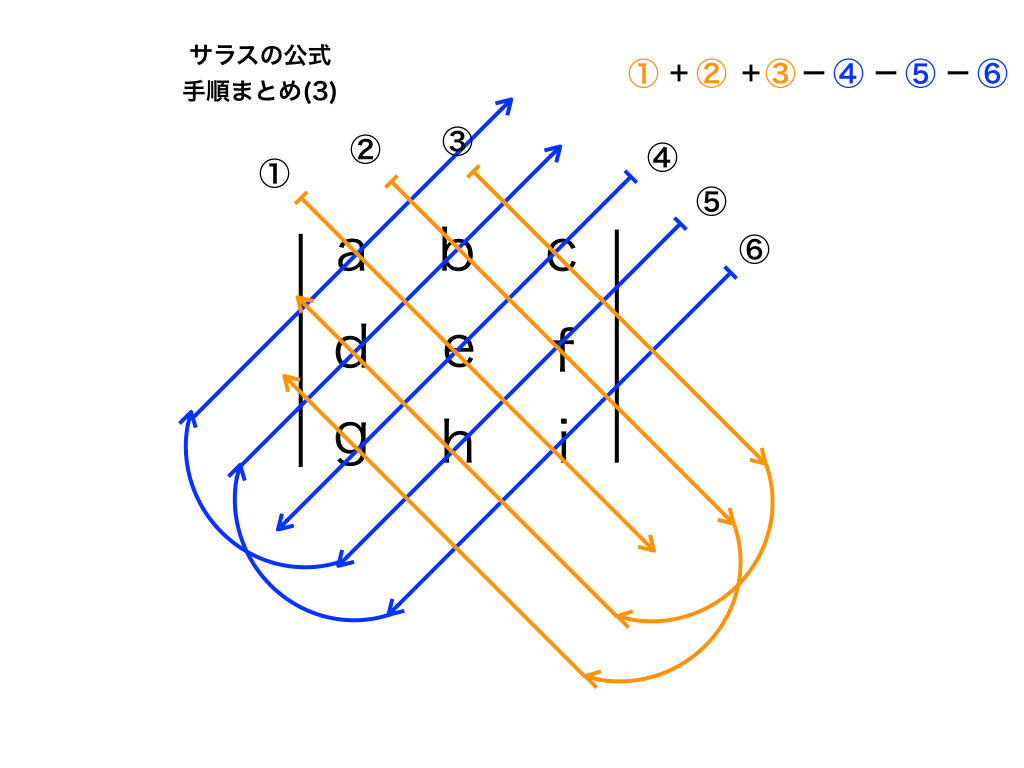
<サラスの公式の手順>
$$\frac{1}{7}\cdot \begin{pmatrix}
-3 & 7 & -8 \\
-1 & 0 & 2 \\
7 & -7 & 7
\end{pmatrix}=\begin{pmatrix}
-3/7 & 1 & -8/7 \\
-1/7 & 0 & 2/7 \\
1 & -1 & 1
\end{pmatrix}$$
右の行列がAの逆行列となります。
ちなみに、ガウスの消去法(掃き出し法)によって逆行列を求める方法は、拡大係数行列 (A|E)を(E|A^{-1})にするように操作を繰り返すことでした。
今回の行列もガウスの消去法を使ってみると、$$\begin{bmatrix}
2 & 1 & 2 & 1 & 0 & 0\\
3 & 5 & 2 & 0 & 1 & 0\\
1 & 4 & 1 & 0 &0 & 1
\end{bmatrix}$$
が$$\begin{bmatrix}
1 & 0 & 0 & -3/7 & 1 & -8/7\\
0 & 1 & 0 & -1/7 & 0 & 2/7\\
0 & 0 & 1 & 1 & -1 & 1
\end{bmatrix}$$ となり、確かに公式で求めた行列と一致します。(復習になるので、ペンを持って実際に計算してみてください!)
余因子行列のまとめと線形代数の記事
・特に3×3以上の行列の余因子行列を作る際は、各成分の符号や行列式の計算・転置などの際のミスに要注意です。
・2or3種類ある逆行列の作り方は、もとの行列によって最短で計算できる方法を選ぶ(少し慣れが必要です)が、基本はやはり拡大係数行列を使ったガウスの消去法(掃き出し法)です。
これまでの記事と次回へ
2019/03/25現在までの線形代数に関する全19記事をまとめたページです。
「【ブックマーク推奨!】線形代数を0から学ぶ解説記事まとめ【更新中】」
今回も最後までご覧いただき、有難うございました。
「スマナビング!」では、読者の皆さんのご意見や、記事のリクエストの募集を行なっています。
ご質問・ご意見がございましたら、ぜひコメント欄にお寄せください。
いいね!やB!やシェア、Twitterのフォローをしていただけると大変励みになります。
・その他のお問い合わせ、ご依頼に付きましては、お問い合わせページからご連絡下さい。