
線形代数学入門シリーズ第9回
<今回の内容>
線形代数(9)となる今回は、はじめに『階段行列』と呼ばれる行列を紹介します。次に、非正則行列に掃き出し法を使用し、連立方程式を解くとどうなるか解説していきます。
<前回の振り返り>
前回「掃き出し法で連立方程式を解く方法」では、連立方程式に対応する行列の行列式が0ではない=逆行列が存在する正則行列の場合を解説しました。
目次(タップした所へ飛びます)
階段行列の意味と掃き出し法
連立方程式を解く前に、『階段行列』とはどういうものなのかを図解していきます。
階段行列とランクとは何か?
階段行列とは、その名のとおり、対角成分を境にして以下の図のように階段状に各成分が並んでいる行列のことを言います。
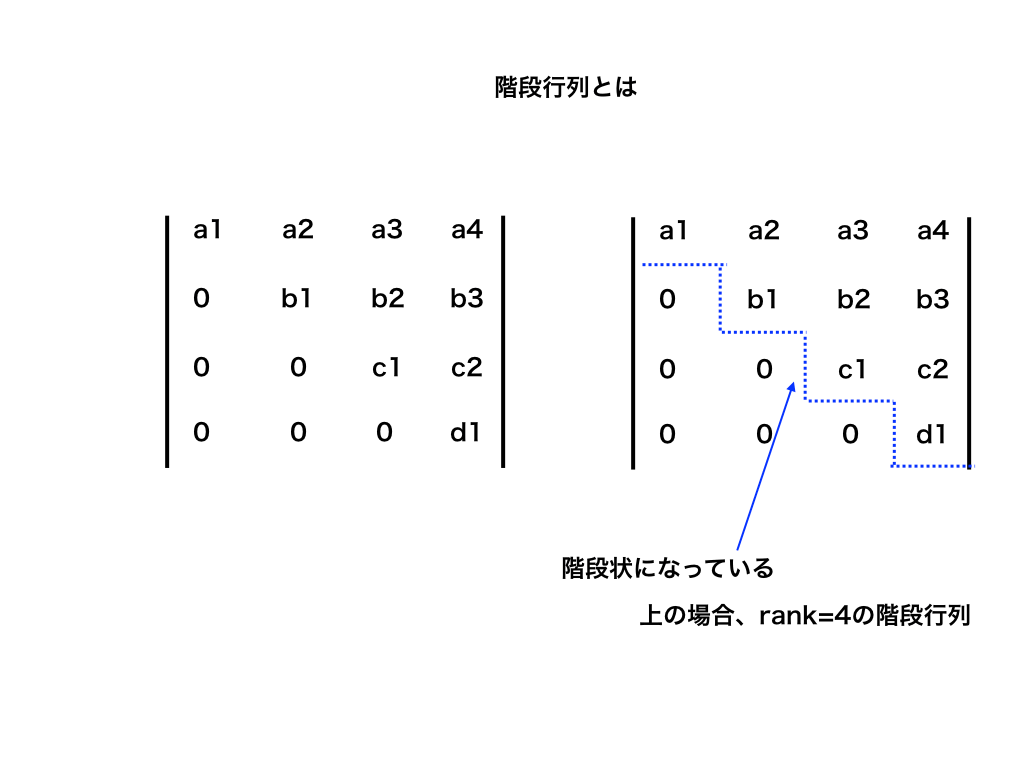
<4×4のサイズの階段行列>
上の図では、4行4列の階段行列を例示しました。右の階段状が4つ並んでいる、この場合をランク(rank)4といいます。(ランクについては、後述します。)
もう一つ、今度は完全な階段状になっていない行列を見てみましょう。
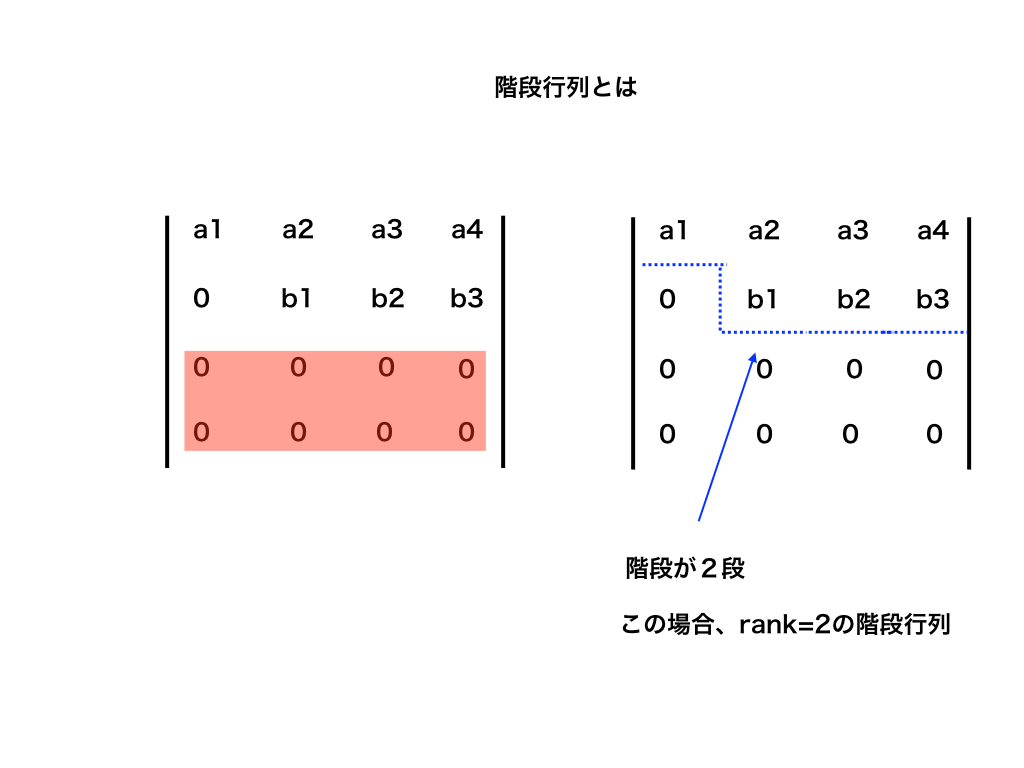
<ランク2の行列>
今度は、階段が2段で下2列は全て成分が0になっています。このような行列をランク2の階段行列といいます。
行基本操作を行って階段行列を作る
例題の連立方程式を階段行列になるように行基本操作を行います。
例:次の三元一次連立方程式の解を求めよ。
4x+2y-2z=0
2x+y-z=0
x+2y+z=0
前回同様、行列の積の形であらわします。
$$\begin{pmatrix}
4 & 2 & -2 \\
2 & 1 & -1 \\
1 & 2 & 1
\end{pmatrix}\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}=\begin{pmatrix}
0 \\
0 \\
0
\end{pmatrix}$$
この行列式を計算すると、(「サラスの公式」より)、$$\det A=|A|=0 $$となり、非正則行列である事がわかりました。
拡大係数行列の形にして、行基本操作を行うと、、
$$\begin{pmatrix}
4 & 2 & -2 & 0 \\
2 & 1 & -1 & 0 \\
1 & 2 & 1 & 0
\end{pmatrix}$$
まず3行目と1行目を入れ替えて、1行1列の成分を1にします。
次に、3行目から2行目を2倍したものを引きます。
$$\begin{pmatrix}
1 & 2 & 1 & 0 \\
2 & 1 & -1 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix}$$
すると、上のように3行目が(0000)の状態になってしまいます。
ここで、2行1列目の成分を0にするために、『2行目ー(1行目×2)』を計算すると、
$$\begin{pmatrix}
1 & 2 & 1 & 0 \\
0 & -3 & -3 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix}$$
最後に2行目を(ー1/3倍)して、
$$\begin{pmatrix}
1 & 2 & 1 & 0 \\
0 & 1 & 1 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix}$$
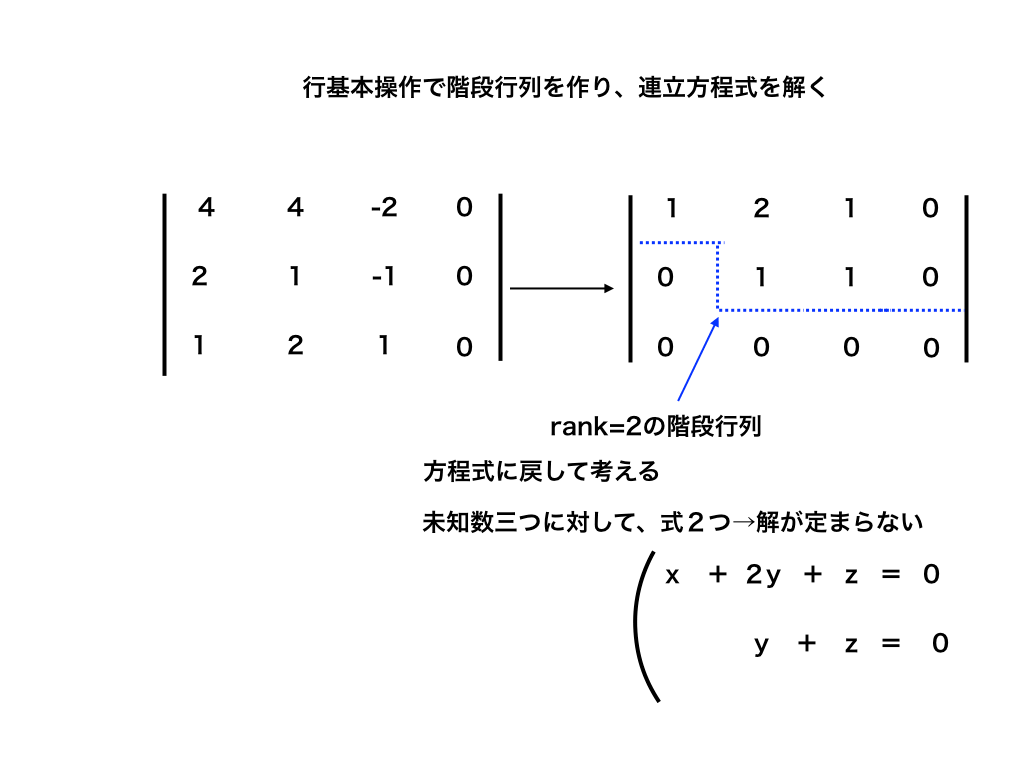
この形で掃き出し法を終了させます。
ランクと自由度・連立方程式の解
上のような操作を経て、階段行列を作り、ランクを求めました。ここでもう一つ重要な『自由度』という数があります。
『自由度』とは、f(自由度)=行数ーランク:で計算できます。
3×3サイズの行列で考えてみると、ランクが3の時(0のみの行がない完全な階段行列)、すなわち自由度=3ー3=0となり、解が1組求まります。
一方で、上の階段行列のように、ランクが2ならば、自由度=3−2=1となり、1つの文字を使って解を表すしかなくなります。
(解が不定なので文字で置く:参照「連立方程式の不定解と不能とは」をご覧ください。)
つまり、この自由度というものは、『解を表すために必要な文字の数』と考えることができます。
だから、ランク3の完全な階段行列にできる(=行列式≠0の)連立方程式は文字を使わずに解を求めることができたのです。
このように、掃き出し法を用いてランクと自由度を求めることで解をしらべることができます。
この記事の最後に、初めに掲載した例題の連立方程式を使って、自由度・ランク・解の求め方を確認しておきましょう。
再掲:次の三元一次連立方程式の解を求めよ。
4x+2y-2z=0・・・(一)
2x+y-z=0・・・(二)
x+2y+z=0・・・(三)
を階段行列に変形して、
自由度=1だったので、適当な文字(ここではsとしておきます)1つで全ての解を表せます。
$$\begin{pmatrix}
1 & 2 & 1 \\
0 & 1 & 1 \\
0 & 0 & 0
\end{pmatrix}$$
このランク2の階段行列をxyzの式に戻すと、
x+2y+z=0
y+z=0
ここで、y=-zであることから、yの解をs(sは実数)として、-z=-s、
1式に、y=sとz=-sを代入すると、
x+2s-s=0
よって、x=-s
ゆえに、例題の3元一次連立方程式の解は、sを使って
(x、y、z)=(-s,s,-s) ・・・(答)
試しに、s=2の時をチェックすると、
(x,y,z)=(-2,2,-2)で、これを(一)に代入すると、-8+4-(-4)=0
(三)に代入すると、-2+4+2=0
となり、確かに満たします。
まとめと次回(掃き出し法で逆行列を求める方法)
・今回はランクと自由度の導入部分を扱いました。今後の記事ではさらに厳密にその意味を考えていきます。
・次回は掃き出し法を使って、解を求めるのではなく、《ある行列の逆行列を作る方法》について解説していきます。
(2×2のサイズの逆行列の作り方と逆行列の基礎的な意味は「逆行列とは?行列の割り算の意味」を参照ください。)
次回予告と線形代数シリーズ
次回は、掃き出し法を利用して逆行列を求める手順を解説します。
→線形代数(3)「逆行列と行列の割り算」の『逆行列の作り方その2』に追記しました。ぜひ続けてご覧ください。
余因子の記事が完成しました。>>「線形代数(10)余因子と余因子展開の意味と応用」<<
これまでの線形代数シリーズは以下のまとめページからご覧いただけます。
>>「0から学ぶ線形代数シリーズまとめ」<<
今回も最後までご覧いただき、有難うございました。
当サイト「スマナビング!」では読者の皆さんの『ご質問・ご意見・記事のリクエスト』をお待ちしています。ございましたら、ぜひコメント欄にお寄せください。
・いいね!やB!、シェア、Twitterのフォローをしていただけると励みになります。
・その他のお問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。

