
対角化と対角行列のべき乗への応用
<この記事について>:2行2列の行列の「対角化」の手順と、その応用として対角行列を利用した、行列のn乗(冪乗)の仕方を解説します。
(※)この記事は、「固有値と固有ベクトルの求め方」の続編です。未読の方は、先にぜひご覧ください。
目次(タップした所へ飛びます)
行列の対角化と対角行列の意味
対角化とは、その名の通り正方行列(:要素の数が、2×2、3×3・・・のように行と列で同じもの)を『対角行列』に変えることを言います。
では対角行列とはどのようなものなのか、そしてどうやって『対角化』するのか具体的に見ていきましょう。
対角行列とは
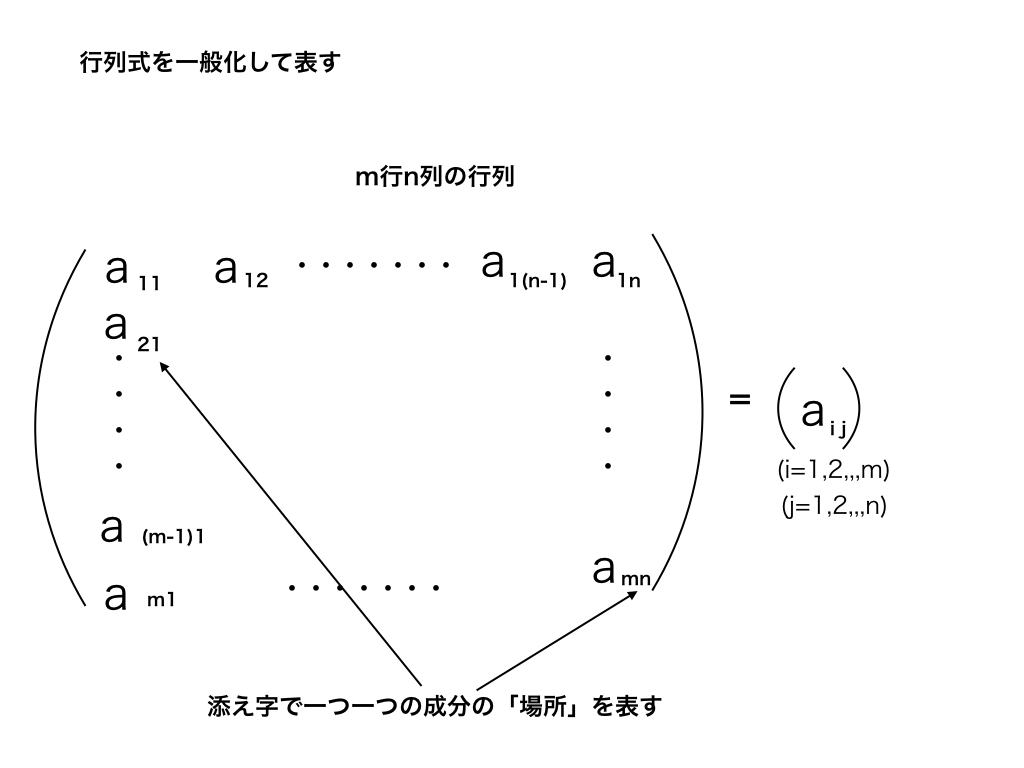
<対角行列の解説図>
対角行列とは、行列の要素のうち、添字が同じ値の($$上の図ではa_{1,1},a_{2,2}・・・$$)要素(=対角成分)にのみ数字で与えられており、
対角成分以外の要素は全て0である行列です。
具体例:$$2行2列の対角行列\begin{pmatrix}
1 & 0 \\
0 & 5
\end{pmatrix}$$
$$3行3列の対角行列\begin{pmatrix}
2 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 1
\end{pmatrix}$$
単位行列Eも、対角行列の一種であると言えます。
$$4行4列のE=\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}$$
対角化の手順
では、実際にどうやって対角行列にするのか前回の記事で扱った、
$$2×2行列B=\begin{pmatrix}
4 & 1 \\
6 & 5
\end{pmatrix}$$を使って説明していきます。
まず、この行列Bの固有値λと、それに対応する条件を満たす適当な固有ベクトルAを
2組見つけます。この手順は「固有値と固有ベクトルを求める手順」で詳しく解説しています。
行列Pを固有値・固有ベクトルより求める。
上記の記事では、λ=2、7;それに対応する固有ベクトルを$$\begin{bmatrix}
1 \\
-2
\end{bmatrix}(λ=2)と\begin{bmatrix}
-1 \\
-3
\end{bmatrix}(λ=7)$$
としました。
ここで、$$行列P=\begin{pmatrix}
1 & -1 \\
-2 & -3
\end{pmatrix}$$
とおきます。(固有ベクトルをそれぞれ縦にならべています)
2:Pが正則行列であるか確認する
次に、行列Pが逆行列P-1をもつ(正則行列)か行列式を計算すると、
(逆行列や、行列式については→「逆行列の求め方と行列式の解説記事」をご覧ください。)
|P|=1・(ー3) ー(ー1) ・ (ー2) =ー5
(ここでの|P|はPの行列式と言う意味です)より、行列式≠0なので、逆行列が存在します。
3:Pの逆行列を計算する。
逆行列の定義より、Pの逆行列$$P^{-1}=\frac {1}{-5}\begin{pmatrix}
-3 & 1 \\
2 & 1
\end{pmatrix}$$
(今回は2行2列の逆行列で考えます。3行3列・・・については「掃き出し法(制作中)」にて詳しく解説します)
追記:2019/03/04掃き出し法での逆行列の計算法について→「逆行列を2通りの方法で求める」で紹介しています。
4:行列BをPとPの逆行列ではさむ
P,P^{-1}が求まったので、対角化する行列BをP^{-1}を左側から、Pを右側から掛けます。
$$→P^{-1}BP=-\frac {1}{5}\begin{pmatrix}
-3 & 1 \\
2 & 1
\end{pmatrix}\begin{pmatrix}
4 & 1 \\
6 & 5
\end{pmatrix}\begin{pmatrix}
1 & -1 \\
-2 & -3
\end{pmatrix}$$
「行列の掛け算の手順」に従って、計算していくとまずP-1Bを計算します。
$$-\frac {1}{5}\begin{pmatrix}
-6 & 2 \\
14 & 7
\end{pmatrix}\begin{pmatrix}
1 & -1 \\
-2 & -3
\end{pmatrix}$$
さらに、右側のPを掛けて、
$$=-\frac {1}{5}\begin{pmatrix}
-10 & 0 \\
0 & -35
\end{pmatrix}$$
行列の前に出ている“-1/5”を各要素にスカラー倍します。
$$P^{-1}BP=\begin{pmatrix}
2 & 0 \\
0 & 7
\end{pmatrix}$$
これで、対角化が完了します。
結果を見てみると確かに対角行列になっており、
かつ対角成分(2と7、)がそれぞれ固有値λの値になっている事がわかります!
対角行列を使って行列のべき乗を求める
さて、固有値、固有ベクトルを求め、対角化を行い『対角行列』が求まりましたが
なんのためにこのような計算をするのか分からない人もいるのではないでしょうか。
実は、この『対角化』をすることで、行列のべき乗(n乗)を簡単に計算することができるのです。
行列のn乗の求め方(対角行列編)
例えば、先ほどの行列Bで考えるとB2,B3,B4…となるにつれて計算が非常に大変になります。
しかし、対角化によって、
$$P^{-1}BP=\begin{bmatrix}
2 & 0 \\
0 & 7
\end{bmatrix}$$
とわかったので、以下の公式を利用する事でグッと楽になるのです。
対角行列のn乗の公式
対角行列のn乗は、各要素(対角成分)のn乗になります。つまり、
$$\begin{bmatrix}
a & 0 \\
0 & b
\end{bmatrix}^{n}=\begin{bmatrix}
a^{n} & 0 \\
0 & b^{n}
\end{bmatrix}…(※)$$となります。
これを数学的帰納法で証明しておきましょう。
(参考→:「数学的帰納法でうまく証明するコツ」)
対角行列のn乗の公式を数学的帰納法で証明する
まず。n=1の時
$$\begin{bmatrix}
a & 0 \\
0 & b
\end{bmatrix}^{1}=\begin{bmatrix}
a^{1} & 0 \\
0 & b^{1}
\end{bmatrix}$$が成立します。
次に、n=kの時
$$\begin{bmatrix}
a & 0 \\
0 & b
\end{bmatrix}^{k}=\begin{bmatrix}
a^{k} & 0 \\
0 & b^{k}
\end{bmatrix}$$が成り立つと仮定すると、
n=k+1の時、$$B^{k+1}=\begin{bmatrix}
a & 0 \\
0 & b
\end{bmatrix}^{k+1}=\begin{bmatrix}
a^{k} & 0 \\
0 & b^{k}
\end{bmatrix}\begin{bmatrix}
a & 0 \\
0 & b
\end{bmatrix}$$
$$(n=kの時の仮定:\begin{bmatrix}
a & 0 \\
0 & b
\end{bmatrix}^{k}=\begin{bmatrix}
a^{k} & 0 \\
0 & b^{k}
\end{bmatrix}$$
より
$$\begin{bmatrix}
a^{k} & 0 \\
0 & b^{k}
\end{bmatrix}\begin{bmatrix}
a & 0 \\
0 & b
\end{bmatrix}=\begin{bmatrix}
a^{k+1} & 0 \\
0 & b^{k+1}
\end{bmatrix}$$
となり、確かにn=k+1でも成り立つ。よって、(※)は証明された。
P-1BP
両辺をn乗するので、$$左辺=P^{-1}BP$$もn乗しなければなりません。
ここで、左辺の2乗を考えてみます。
$$(P^{-1}BP)^{2}=(P^{-1}BPP^{-1}BP)$$
丁度、$$中央のPP^{-1}が単位行列Eになる$$事がわかりますね!
式を整理すると$$=P^{-1}BEBP=P^{-1}B^{2}P$$
次に、左辺の3乗を調べると
$$(P^{-1}BP)^{3}=(P^{-1}BPP^{-1}BPP^{-1}BP)$$
$$P^{-1}BEBEBP=P^{-1}BBBP=P^{-1}B^{3}P$$
このように、左辺は何乗しても$$P^{-1}B^{n}Pとなります。$$
左辺と右辺を合わせると・・・
両辺のn乗の式を書き出すと、
$$P^{-1}B^{n}P=(対角行列)^{n}=\begin{pmatrix}
λ^{n}_{1} & 0 \\
0 & λ^{n}_{2}
\end{pmatrix}$$
ここまで来れば、行列のべき乗の計算もあと少しです。
左辺にある、不要なPの逆行列とPを両辺の左右からかけて消してあげると、
$$PP^{-1}B^{n}PP^{-1}=P\begin{pmatrix}
λ^{n}_{1} & 0 \\
0 & λ^{n}_{2}
\end{pmatrix}P^{-1}$$
$$=B^{n}=\begin{pmatrix}
1 & -1 \\
-2 & -3
\end{pmatrix}\begin{pmatrix}
2 ^{n} & 0 \\
0 & 7^{n}
\end{pmatrix}\frac {1}{5}\begin{pmatrix}
-3 & 1 \\
2 & 1
\end{pmatrix}$$
このように、対角行列を利用する事で、非常に簡単に行列のn乗(べき乗)を求めることができます。
まとめと続編(連立方程式と行列・掃き出し法)へ
今回は、特に分量も多く一気に理解するのは大変かもしれません。じっくりと「固有ベクトルと固有値の求め方」などの関連記事と往復して読み込んでみてください。
そして、ある程度理解できたら実際に固有値・固有ベクトルを求めるところから、対角化を経てn乗の式を作る作業を実際に手を動かして練習しましょう。
続編:「連立方程式を行列を使って解く方法」の記事が完成しました。
線形代数超入門シリーズ一覧
線形代数超入門:第0回「集合と写像:単射・全射・全単射」から、現在までの線形代数に関する記事は
>>『線形代数とは?0から学べる入門記事の総まとめページ』<<にまとめています。わからない所があれば、その都度確認してみてください。
今回も最後までご覧いただきまことに有難うございました。
お役に立ちましたら、シェアと公式Twitterのフォローをお願いします。
・記事のリクエストとご質問・ご意見はコメント欄にお寄せください。
・より良いサイト運営・記事作成、更新の為に是非ご協力お願い致します!
・その他のお問い合わせ/ご依頼等はお問い合わせページよりお願い致します。

