
三角関数の公式の覚え方/証明一覧
三角関数の公式を最小限の記憶(加法定理)と、”加法定理から全ての公式を導く方法“をインプットしておくことで、覚える量を激減させるだけでなく、試験中に忘れるといった心配も無くなります。
この記事では、それらの基本である三角比についての復習も行います。
目次(タップした所へ飛びます)
三角関数のキソ三角比の値と各種基本公式
最新版
三角比の簡単な復習
以下の図を使って三角比の簡単な復習をしていきます。
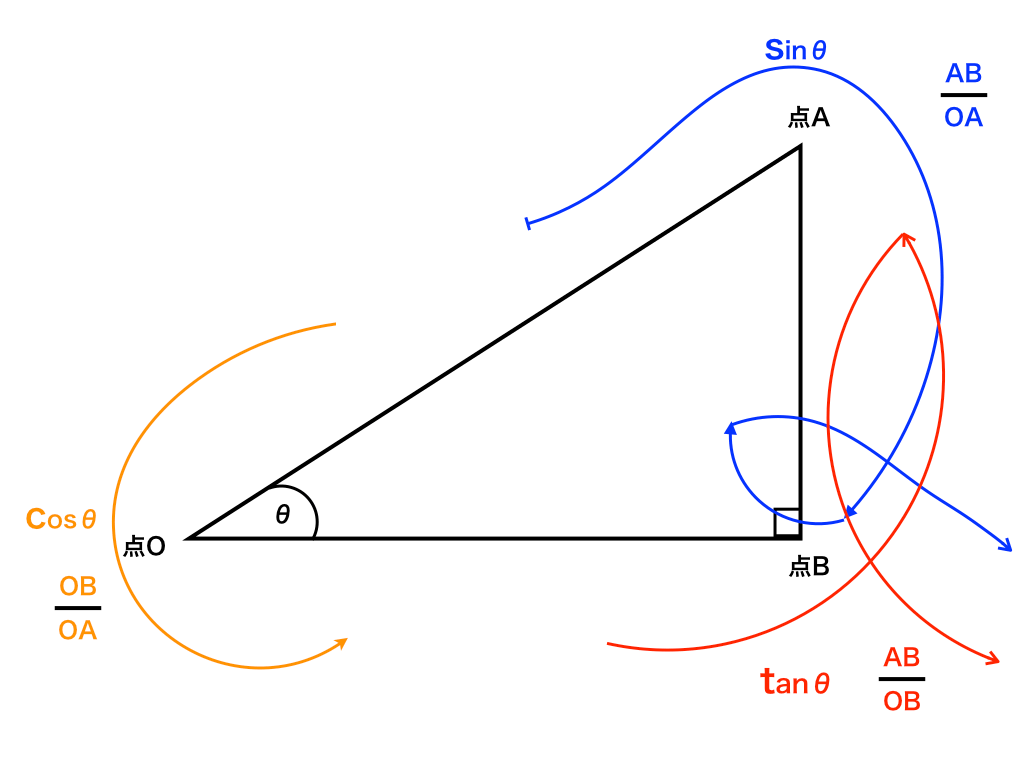
<サイン・コサイン・タンジェントの値>
上の図で説明すると、サイン・コサイン・タンジェントは、角θを左、直角∠OBAを右側にし、$$sinθ=\frac{AB}{OA},cosθ=\frac{OB}{OA},tanθ=\frac{AB}{OB}$$と、それぞれの頭文字(sin→s,cos→c,tan→t)の小文字の筆記体を書くようにすることで悩まず求めることができます。
正弦・余弦定理
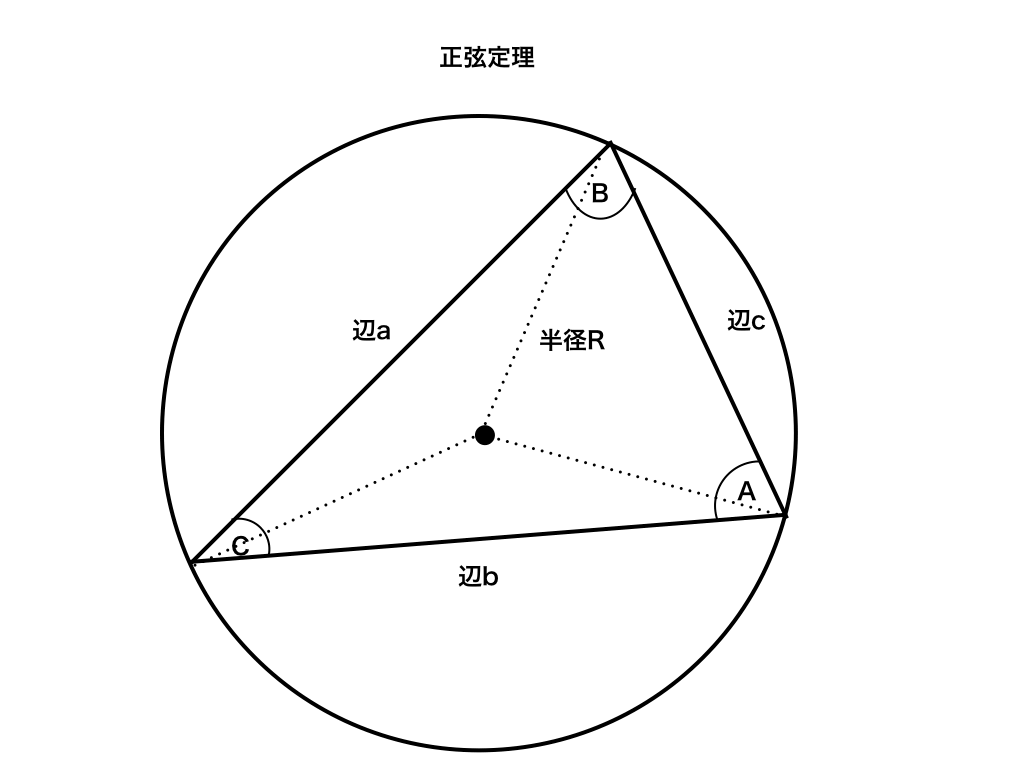
<正弦定理>
正弦定理は、半径Rの円に内接する三角形の角度ABCと辺abcを正弦(=サイン)で結びつけたもので、次のように表されます。
$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$$
「ある角の正弦(sin)ぶんの対辺の長さは全て等しく、その値は半径の二倍、つまり直径と同じ値をとる」という意味です。
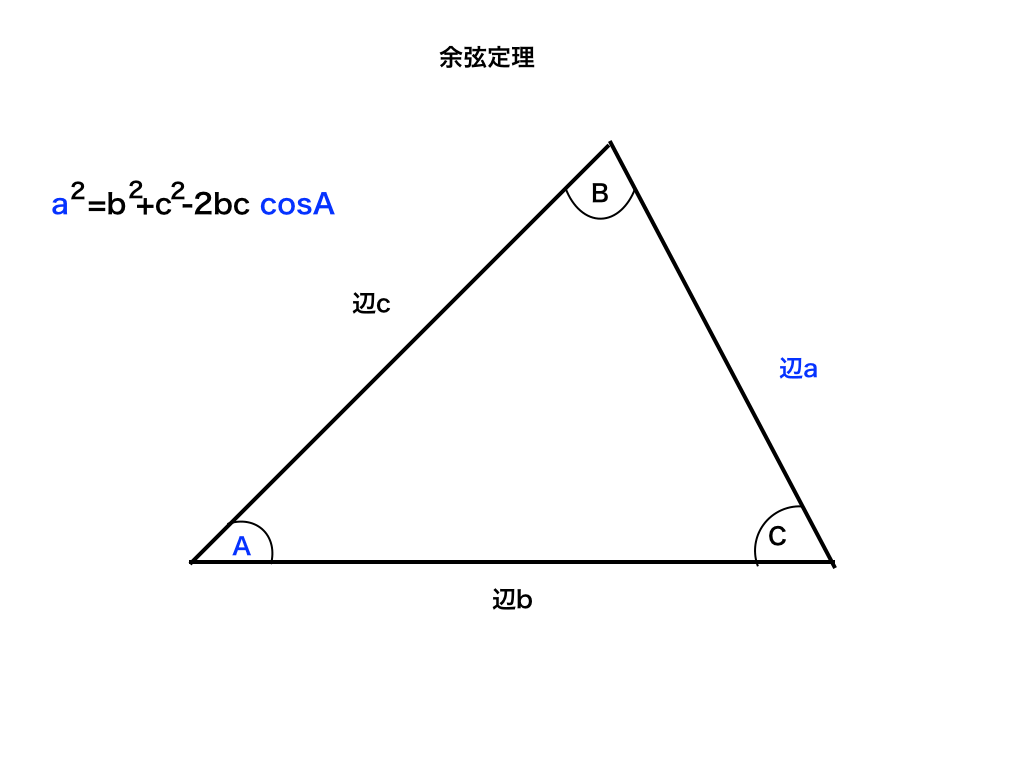
<余弦定理>
余弦定理も、その名が表すように余弦(cos)が関係し、ある辺(上の図ではa)の2乗=残りの辺の二乗の和(b2+c2)マイナス2bc×cosA(このAは”ある辺”の対角です)という式で表されます。
残りの辺の余弦定理も同様に、
\(b^{2}=a^{2}+c^{2}-2ac\cos A\)
\(c^{2}=a^{2}+b^{2}-2ab\cos C\)
となります。
度数法での三角比の値一覧
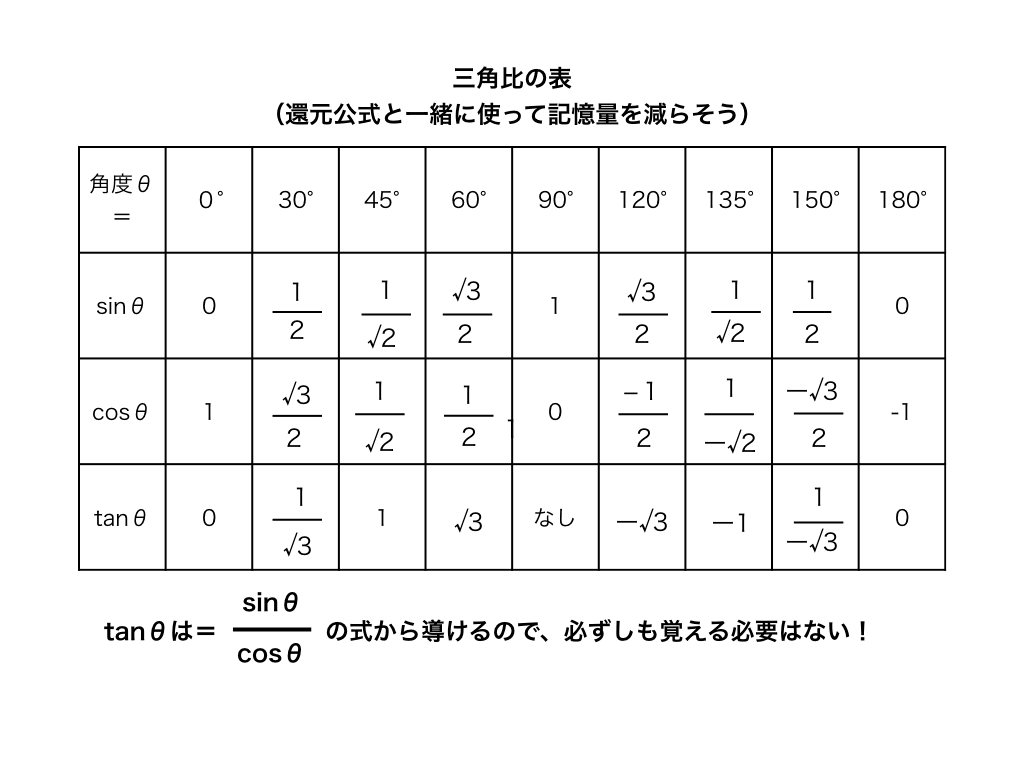
以上の三角比とその関連公式などについては、「三角比の表/正弦・余弦定理をわかりやすく解説」←こちらの記事で詳しく紹介しています。
三角関数の式とグラフの描き方
y=AsinB(θ+π)のような、周期や振幅・位相(詳しくは以下のページで紹介しています)が複雑な三角関数の式を与えられた時に、うまくグラフを書く方法を解説しました。
・・・・・・・・
公式編へ向かう前の注意点
注)公式の丸暗記はお勧めできません!
公式を丸暗記していると、試験中少し捻られた問題にぶつかったり、ド忘れしてしまった時に、その問題だけで無く他の大問にも心理的な影響を与えてしまう恐れがあります。
実際、以下の記事でも解説していますが、平均点39点だった2015年センター数学2B、平均点41点だった1998年センター数学2B共に三角関数の問題(しかも公式に関する問題)でした。
では始めます。注意事項を守って、ぜひ【三角関数の公式のポータルページ】としてご利用ください!
三角関数の公式まとめ記事一覧
まず、余弦定理を使って【全ての三角関数の公式のもと】になる『加法定理』を証明・記憶します。
そこから
・二倍角の公式/三倍角の公式/半角の公式
・和積の公式/積和の公式
・三角関数の還元公式
・三角関数のsin型とcos型の両方での合成
をそれぞれ加法定理より導きます。
三角比の相互関係プラスα
上ですでに触れていますが、これから諸公式を導く際に「道具」になるものや、数1Aではそれ自体が問題になる正弦定理・余弦定理をまとめました。
弧度法の意味と180°=π(rad)の理由
数1の三角比は度数法(°で表す)でしたが、数2以降の三角関数では『弧度法』が基本になります。
したがって、意味をしっかり理解できていないと言うことがない様に、「弧度法の意味・定義と180°=π(rad)になる理由」で曖昧な部分をチェックしておきましょう。
全てはココから!加法定理
サインの加法定理:\(\sin \left( \alpha \pm \beta \right) =\sin \alpha \cos \beta \pm \cos x\sin \beta\)
“ほとんどの公式は加法定理から導ける”ほど重要な定理です。
従って、「最重要公式:加法定理の証明と応用」の記事でまず証明法(作り方)をしっかり理解した上で、記憶しておきましょう。
 <三角関数の加法定理一覧>
<三角関数の加法定理一覧>
半角/二倍角/三倍角の各公式を導く
数学2ではもちろん、数学Ⅲの積分でも大活躍する公式たちを、加法定理から導出します。
その方法は、「加法定理から半角/二倍/三倍角の公式を導く」←の記事で詳しく解説しています。
二倍角の公式の一例:\(\sin 2\alpha =2sin\alpha \cos \alpha\)

で<2倍角の公式>と

<3倍角・半角の公式>
\(\sin 3\alpha=3\sin \alpha-4\sin^{3} \alpha\)
\(\cos 3\alpha=4\cos^{3} \alpha-3\cos \alpha\)
積和の公式・和積の公式はその場で作る!
積和の公式/和積の公式は種類が多く、式も複雑でややこしいので、基本的に加法定理のペアをもとに、必要なときにその場で作る事→「積和/和積の公式は覚えるな!その場で導く方法」をお勧めします。
三角関数の余角・負角・補角の公式は2STEPで攻略!
いわゆる還元公式と呼ばれるもので、全部で18種類以上あります。
この公式も覚えるよりも導いた方が良いので、sin(θ+90°)やcos(θ±π)などを瞬時に変換する方法を、「三角関数の余角/負角/補角の公式の攻略法」こちらの記事で”鋭角を代入する方法”と”加法定理を使う方法”の2パターン紹介しています。
sin型とcos型のどちらでも三角関数の合成をできる様にする方法
\(合成の例:\sin \theta +\sqrt {3}\cos \theta =?\)
上の式をsin型でも、cos型でも合成する方法を
→「三角関数の合成公式:これさえ読めばcos型でも楽々解ける」で解説しています。
ぜひご覧ください!
なお、冒頭に述べたセンター数学2Bが壊滅的だった年はいずれも合成と加法定理の関係をしっかり理解できているかを問うものでした。
追記:加法定理の暗記について
(追記:結局加法定理は暗記するのか?という意見を頂きましたので、筆者の考えを書かせて頂きます。
加法定理は「他の三角関数の公式を導出する際に全ての起点となる」という点で、使用頻度が格段に多いため、
加法定理だけは自力で証明できる様になった段階で、覚えておく方が効率が良いと考えます。
毎回証明しても良いですが、試験中に『加法定理の証明→加法定理から他公式を導出』するのは現実的ではないからです。
また、証明を伴わない丸暗記と、いつでも証明(導出)出来る状態で覚えておく事には、大きな差があると考えています。)
以上で高校数学における【三角関数の公式】はほぼ全て網羅できます。
必ず自力で導出できる様になるまで『理解してから使う』様にして下さい!
三角関数の関係する範囲のまとめページ
三角比・三角関数以外の分野で融合問題が出題されやすく、かつ、ニガテな人が多い単元の解説ページをまとめました。
三角関数が関わる方程式と不等式
極限(数三)と微分・積分
三角関数の極限や微分・積分、さらにその応用などで関連する記事のまとめです。
ベクトルが苦手な人は是非ご覧下さい!
ベクトルの内積や、なす角、平面/空間図形の問題において三角比/関数を非常によく利用します。
今回も最後までご覧いただき有難うございました。
お役に立ちましたらシェア&当サイト「スマホで学ぶサイト、スマナビング!」公式Twitter(@linkyjuku_tweet)のフォローをお願いします!
また、記事のリクエスト・ご質問・ご意見はコメント欄にお願いします。
それ以外のお問い合わせ/ご依頼は、お問い合わせページよりお願い致します。

