
波の式の作り方
今回扱う波動範囲は、高校物理の中でも苦手意識をもつ人が多い分野です。
更に、その中でも正弦波の式(波の方程式)の作り方は一見すると難しそうに感じます。
しかし、実際には解き方が決まっているので、この記事を読んでstep by step で付いて来てもらえれば、自分で波の式を作れるはずです。
目次(タップした所へ飛びます)
波の式の意味
※この記事は、力学の単振動を既に習っている事を前提にしています。
単振動を未習の方は、以下の記事で詳しく解説しているので先にご覧ください!
では早速始めます。
波に関わる2種類のグラフ(形)の意味と用語の確認
波の方程式ではyーtグラフとxーyグラフがよく出てきます。この2つは似て非なるものなので、
媒質の単振動のグラフ(yーtグラフ)と、波全体の瞬間のグラフ(xーyグラフ)を混同しない事が重要です。
よくある例えですが、コンサートなどでのウェーブを考えてみて下さい。
ウェーブは一人一人が立ったり座ったりして(上下に動いて)次にとなりの人も少し遅れて上下に動いて・・・という運動をしています。
それをステージなどから見ると波が起きている様に見えるわけです。
ここでの媒質は人です。人が時間timeとともに上下(y軸に平行)に運動している、これが正にyーtグラフです。
一方、ステージから見た波はその「瞬間」の波の形を表しているので時間t(time)が関係ない(xーy)グラフに当たります。
波の方程式の形の意味と作る目的
次に、見通しをよくする為に、求める波の方程式の形と‘何のために必要なのか’を先に確認しておきます。
少し難しいですが、ウェーブの例と照らし合わせて読んでみてください。
波の方程式は、y=y(x,t)の形をしています。ここでのyはシンプルにy座標です。
そしてy(x,t)は、位置が"x座標"、時刻"t"での"媒質のy座標"という意味です。
つまり波の方程式さえあれば、【任意の場所(x)にある媒質】(先程の例だとウェーブをしている人)が、【任意の時間(t)に】、どの【y座標(どれ位立っているか)にいるか】がわかる様になる
=波を構成しているどんな媒質の運動もわかる様になる!のです。
前提知識:三角関数のグラフ
ここからは、三角関数とそのグラフ、周期、振幅、位相などの(数2)レベルの知識が必要です。
確認したい方は、先に「三角関数の式からグラフを作る:平行移動/振幅など」をご覧下さい!
正弦波の式の作り方の手順
では、実際に式を作る手順とテクニックを以下で紹介します。
y-xグラフから情報を読み取って、媒質の単振動の式を作る
次に全体の波のグラフから式を作って見ましょう。初めは媒質の単振動の式を作って行きます。
先に述べた通り、媒質は上下に単振動しているので、任意の時間tでのyの位置を表す式は、振幅をA、角振動数をω、時間をtとして
\(y=\pm A \sin \omega t\)
\(y=\pm A\cos \omega t\)
y=±A sinωt または、y=±A cosωt と表せます。
ここで良くある質問のとして、符号は±どちらか?とsin/ cosのどちらを選べばいいか良くわからない!というものがあります。
step1:全体のグラフを少しずらせ!
そういう場合は、波の進行方向が与えられているのでその方向へ少しだけ「ずらして」みます。
図1の様に右方向へ進む波(実線)のxーyグラフをずらすと、
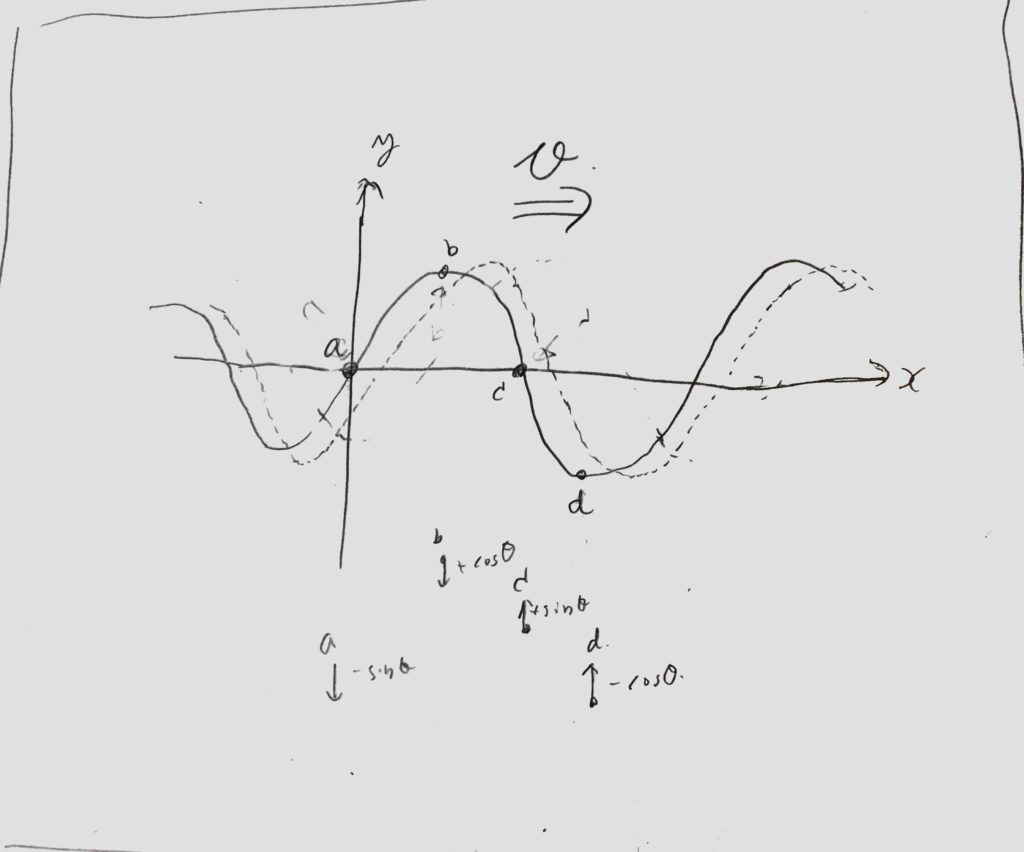
<図1:波(y-x)グラフをずらす>
少しだけ時間が経った時、波は点線の様に見えます。
この時、媒質のx座標は変わらずy座標のみが動く(上下に単振動)ので、原点にいる媒質をaとすると、aは少し時間が経った後に下向きに動いています。
step2:ずらした図をもとに三角関数を選ぶ
ここで、±sin/± cosの4種類から、はじめの位置が0で下方向へ動くグラフを考えると−sinの形しかありません。
よって、aのy座標はtを用いて、\(y=-A\sin \omega t\)
y=ーAsinωt と表すことができました。
「悩んだら少しずらす」考え方はとても大事なのでぜひ身につけて使って行って下さい!
原点での媒質の式をどの位置でも使える様に一般化する
いま、y=ーAsinωt で表したのは、原点でのaの運動の式で、y=y(t)の式です。
我々が求めないといけない方程式は、y=y(x、t)でした。
つまり上の式には【位置xの情報が欠けている】のです。
そこで、どの位置(x)でも使える式に変える為に、式を少し改造します。
例として先ほどの図のbの運動を考えてみます。bでは、aで起きた運動が遅れて起こります。
(ウェーブを考えてみると、一番端の人が最初に立ち上がって、徐々に遅れて隣の人が同じ様に立ち上がります。)
step3:「遅れ」を考慮してtの部分を変換せよ!
そこで、場所(x)での“遅れ”を考慮して、波の速さがvだから、\(y=-A\sin \omega t\)
を、$$\begin{aligned}y=-A\sin \omega \left( t-\frac {x}{v}\right) \\
\left( t\rightarrow t-\frac {x}{v}\right) \end{aligned}$$
y=ーAsinωt をy=ーAsinω(t–x/v)と書くことが出来ます。
変型した部分は、t→tーx/v で、これは『原点からx離れた場所での媒質の運動は、原点で(x/v)秒「前」に起きた運動と同じこと(波の速さがvより)』を表しています。
これでy=y(x,t)の式を作る事が出来ました!
これでも問題無いのですが、もう一つ、別の形の波の方程式を問われることがあります。
Tを周期、λを波長、fを振動数として、波に関する公式 v=fλ と ω=2π/T と T=1/f より、
$$v=f\lambda ,\omega =\frac {2\pi }{T},T=\frac {1}{f}$$
y=ーAsinω(t–x/v)・・・(1)
⇔y=–A sin(2π/T)(t–x/v)
$$y=-A\sin ( \frac {2\pi }{T}) ( t-\frac {x}{v}) $$
⇔y=ーAsin2π(t/T–x/Tv)
$$y=-A\sin 2\pi ( \frac {t}{T}-\frac {x}{Tv}) $$
$$Tv=( \frac {1}{f}) \times ( f\lambda ) =\lambda $$
ここで、Tv=(1/f)・(fλ)=λだから、
y=ーAsin2π(t/T–x/λ)・・・(2)
$$y=-A\sin 2\pi ( \frac {t}{T}-\frac {x}{\lambda }) $$
問題では(1)or(2)どちらかで答えさせるので、どちらを聞かれても導けるようにしておきましょう。
物理:波動分野で悩んでいるひとへ【光波の干渉/ドップラー効果】
冒頭にも書いた通り波動は難しいと感じやすいです。
そこで、波動分野の中でも特に差が付く記事を書きましたので、是非ご覧下さい!
「光波の干渉実験(ヤング/薄膜/くさび形空気層の干渉実験)を攻略するたった2つの事」
お役に立ちましたら、SNSボタンでシェアお願いします!
その他のお問合わせ・ご依頼等は【運営元ページ】よりお願いします。

