
複素数平面(数学Ⅲ)を総まとめ!
<このページは、数二の複素数から復習し、苦手な人が多いが実はとても便利な【複素数平面(ガウス平面)】の解法・解説記事を、内容・レベル毎にまとめたものです。>
目次(タップした所へ飛びます)
複素数とは(step0)
数学IIの範囲から復習していきます。(基礎的な内容なので、不要な方はstep1へ進んでください。)
2次方程式の解の公式と複素数
さて、二次方程式の解を求める際には、\(\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}\)と言う”解の公式”を用いました。
また、実数解の有無や、重解があるかを調べるときには、\(判別式D=\sqrt{b^{2}-4ac}\)を用いました。
しかし、判別式の中身がマイナスになる、すなわち\(b^{2}<4ac\)の時にはルートの中が負になるため、解の公式が使えませんでした。
虚数i
ここで登場するのが”二乗すると負になる”数:虚数単位\(i\)です。
このような数は実数の世界では存在しませんが、この虚数を作ったことで、判別式が0未満であっても(一応)解を計算できるようになりました。
複素数と実数・純虚数
さて、次に『複素数』の復習です。以下のように複素数という大きな括りの中に、(1)実数と(2)『実数+虚数』、さらに虚数のみの(3)『純虚数』が存在します。
(1)の例:2、\(\sqrt{3}\),\(\frac{2}{5}\),,,
(2)の例:3+2i,\(\sqrt{2}-5i\),,,
(3)の例:5i,-3i,\(\frac{4i}{7}\),,,
これまでは、(1)の実数の世界だけしか扱ってきていなかったことを考えると、複素数を導入することによって”一気に世界が広がる”ということをこれから具体的な記事で実感してもらえればと思います。
1の3乗根:ω
step0の最後に、三乗すると『1』になる数のうち”1”ではない2つの複素数を表す「オメガ:ωの意味と使いかた」をまとめて解説しました。(一部数学3の範囲も入っています。)
複素数平面の基礎まとめ(step1)
ここからは、数学Ⅲの複素数平面(本題)に入っていきます。まず複素数平面とは何か?という記事から始めます。
複素数平面と極形式⇔直交形式
早速step1のはじめの記事を見てみましょう。
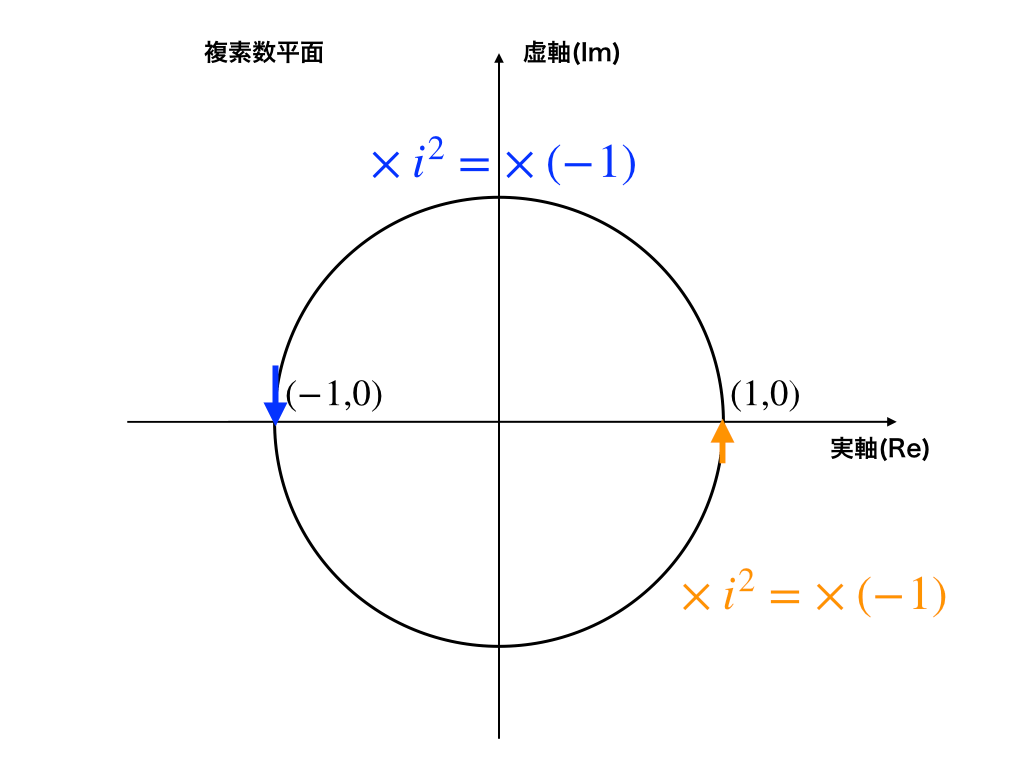
「複素数平面とは?直交座標(形式)と極座標(形式)の意味と相互変換」←の記事では、聞きなれない”極形式”・”極座標”といったものの意味、従来の座標との対応と相互変換の仕方を学びます。
極形式での積と商(回転)
次に、上で学んだ複素数の極形式どうしを掛ける(積)ことや、割ること(商)がどのような意味を持つのかを「極形式での積と商、そして回転の関係」で紹介していきます。
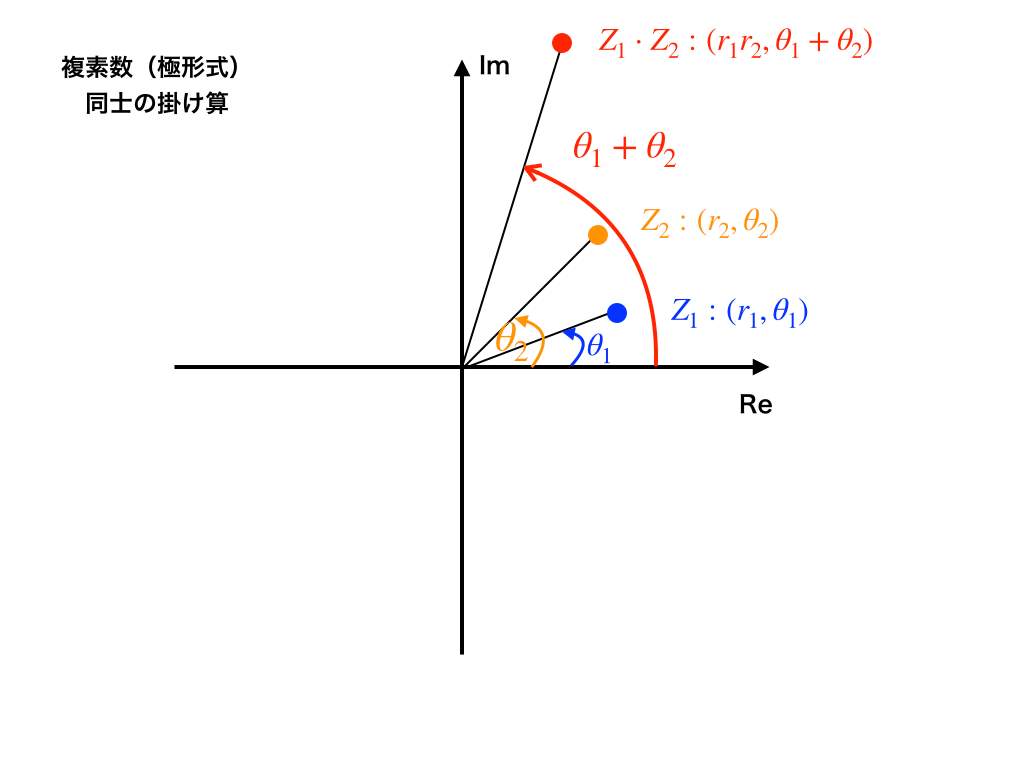
なお、上の記事では証明に「三角関数の加法定理の記事(参考)」を用いています。
ド・モアブルの定理と証明
このstepの最後は、複素数平面の単元の中でも最重要の定理と言っていい、『ド・モアブルの定理』の意味と使い方について解説しています。「ド・モアブルの定理とその応用」
(数学1の論理と集合の分野で扱う『ド・モルガンの定理』とは全く異なるので念のため・・・)
複素平面上の図形(step:二)
さて、step0、step1によって複素数平面の基本的な意味や計算に少し慣れてきたでしょうか?
ここからは複素数(平面)の知識を使って、図形に関する問題を解く方法を紹介していきます。
内分点と外分点の位置
まずは、普通の図形の分野でも苦手な人が多い内分・外分点についてです。「内分点と外分点の位置の見つけ方(複素平面編)」
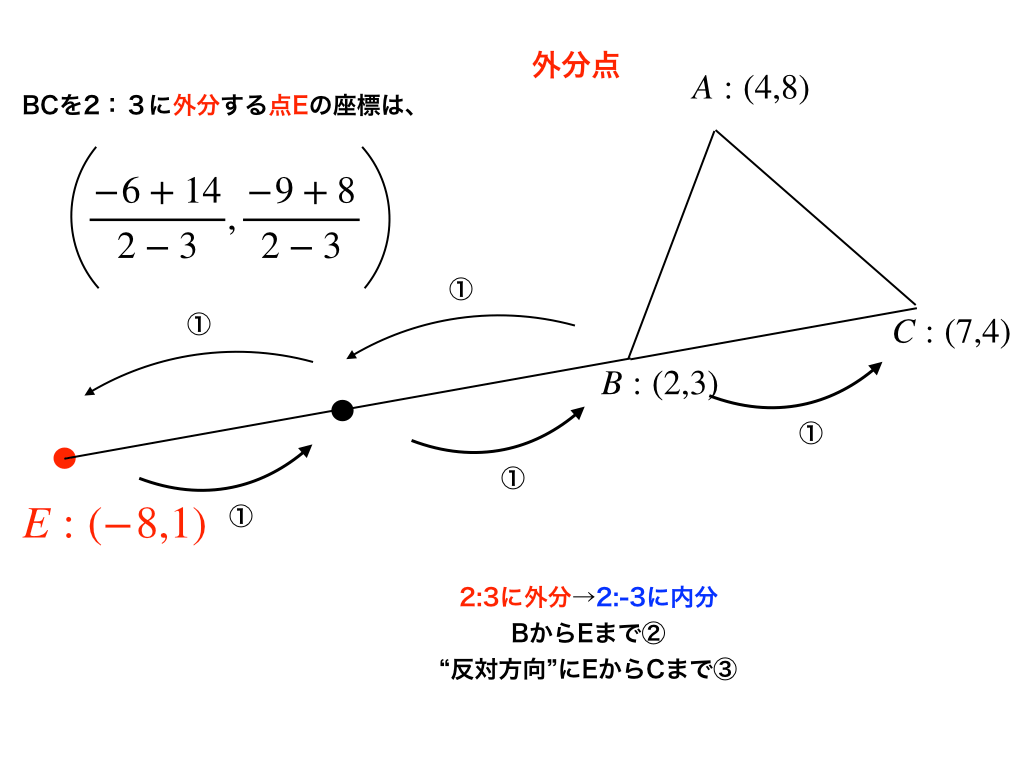
内分・外分はベクトルなどでも頻出ですが、特に外分点に関しては『公式は覚えているけれども、位置を図示できない』という人が多いので、図示の手順にも詳しく触れています。
円の式と軌跡(1)/アポロニウスの円
複素数で表された式がどのような図形を描くのか、また、軌跡(図形と方程式)として扱われている分野の問題を複素数平面で解く方法(基礎編)を「複素数平面での円と条件を満たす図形」で紹介しました。
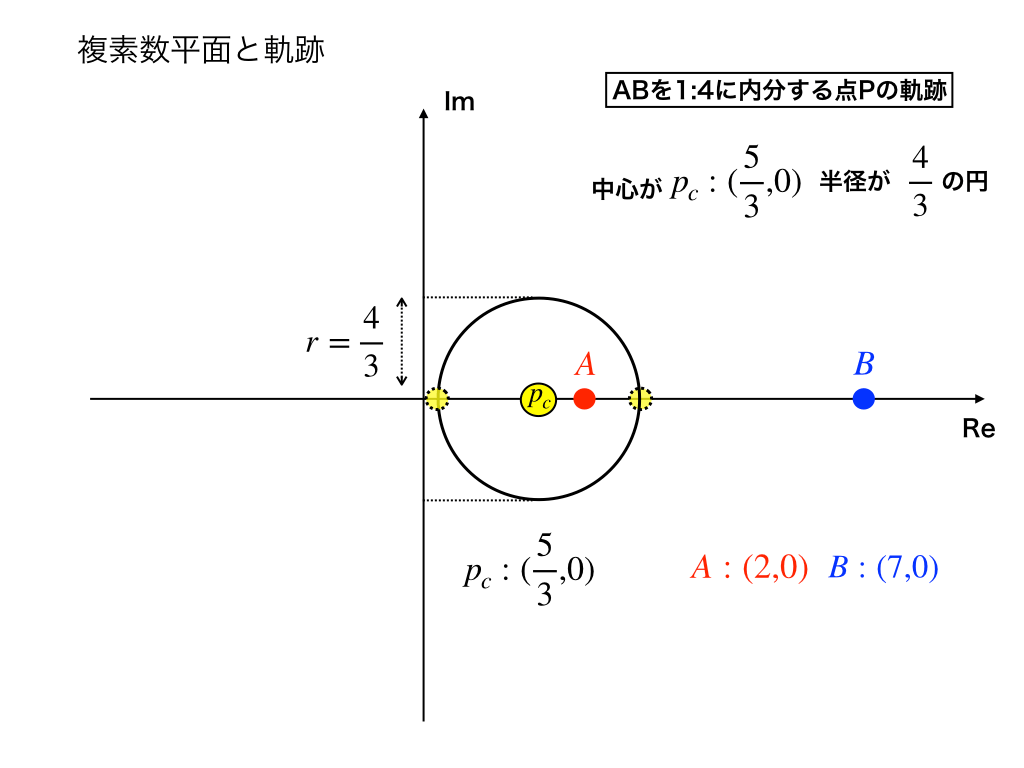
直線のなす角と直交条件
”回転”の応用として、原点以外を中心とする回転を解説し、さらにそれを利用して
・『二直線のなす角の求め方』や
・『直交/共線条件』について「複素数平面(6):二直線のなす角と直交条件」で解説しています。
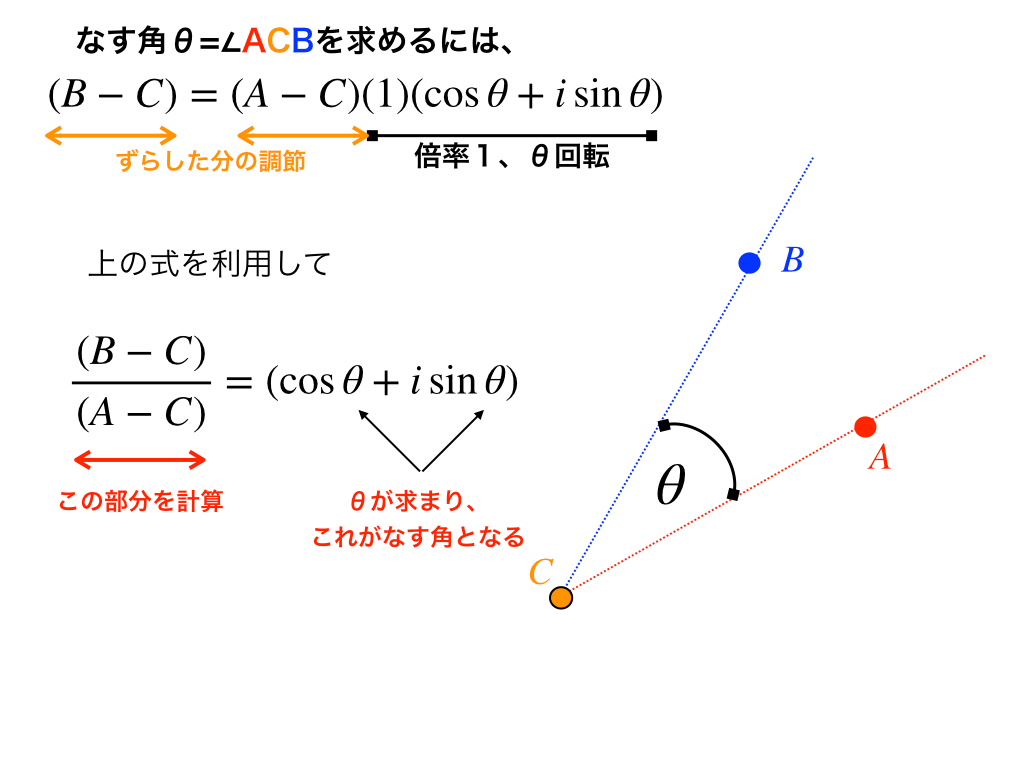
この他にも、なす角を求めるには正接(tan)を利用したり、ベクトルを使うなど複数の解法があります。(詳しくは『関係の深い分野』参照)
・・・随時更新中・・・
図形問題の解法で関係が深い分野
いろいろな記事で述べているのですが、図形の問題は『数A:図形の性質』以外にも様々な分野の知識を応用することで解くことができ、1つの問題に3通りや4通りの別解があることはごく普通です。
それらの複数の解法から最適な方法を見極め、正確に解けるようになる為には、
・一通りそれぞれの単元の学習が終わるごとに、『ベクトルで解けた問題を複素数平面を使って解けないか?』と考えてみるなど、
・いくつもの分野の(解法の)引き出しを持った上で常に試行錯誤しておくことが重要です。
ここでは、図形問題へのアプローチの手段としてメジャーなものを挙げ、関連するまとめページを紹介していきます。
図形と方程式
複素数平面や以下で紹介するベクトルと共に、図形を扱う分野です。
「軌跡と領域」など、難しい単元もありますが、「図形と方程式の解法記事・公式集のまとめページ」←でわかりやすく解説しています。
ベクトル
ベクトルは図形、特に空間図形に対して非常に有効な道具です。
右の記事→「ベクトルとは?0から意味や解法を解説した厳選12記事まとめ」では、ベクトルの意味から応用問題の解法や定石などを紹介しました。
三角比・三角関数
三角比・三角関数も図形問題と相性が良く、ベクトル・複素数平面を解く際にもなくてはならない単元です。
次の記事では、主に”三角関数の公式”を覚えず導く方法をまとめています。
「三角関数の公式は暗記厳禁!覚えず導く方法まとめ」これらの公式を自由自在に操ることができれば、解法の幅はグッと広がります。
行列(現行過程外ですが重要です)
行列という単元は旧課程の数Cに存在しましたが、現行過程では扱われていません。
しかし、ベクトルと同様に行列の考え方は単に問題を解くだけでなく、ありとあらゆる所で利用されています。
興味のあるハイレベル生はぜひ時間のあるときに読んでみてください。
(線形代数という学問で行列を扱い、大学では学部1年で学びます)
今回も最後までご覧いただき、有難うございました。
当サイト:「スマナビング!」では、読者の皆さんのご意見や、記事リクエストの募集を行なっています。
ご意見/ご感想がございましたら、ぜひコメント欄にお寄せください。
お役に立ちましたら、B!やSNSでシェアをしていただけると励みになります。
・その他のご依頼などに付きましては、お問い合わせページからご連絡下さい。

