
1の3乗根=ωをまとめて解説(数2/数3)
<この記事の内容>:ωの基本的な意味の解説から頻出問題・計算問題対策、複素数平面でのωまで高校数学で必要なオメガの知識をまとめました。(コンテンツ追加中)
<参考記事>:「虚数単位iから複素数平面の応用まで解説記事まとめ」
目次(タップした所へ飛びます)
ω(オメガ)とは?
そもそも\(\omega\)とはどのような数なのでしょう?
『1の3乗根』
ω:オメガは1の3乗根で1以外のものと言えます。
言い換えると、3乗したら1になる数の内“1”を除くものという意味です。
つまり、\(x^{3}=1\)を満たすxかつ、x=1以外のものを特別に”オメガ”と名付け、ギリシャ文字の”ω”で表しているのです。
実数の範囲で考えれば、3乗したら1になる数は1だけですが、虚数単位iを導入して複素数の世界でもωの値を調べてみましょう。
因数分解と解の公式でωの値を求める
\(x^{3}=1\)なので、\(x^{3}-1=0と移項して\)因数分解していきます。【参考記事:「因数分解の手法総整理!必須公式と因数定理etc,,,」】
すると、\((x-1)(x^{2}+x+1)=0\)より、x=1(これは上で挙げた1です)そして残った\((x^{2}+x+1)=0\)の値は因数分解できないので、解の公式を使用します。
従って解の公式より、$$\frac{-1\pm \sqrt{1^{2}-4\cdot 1\cdot 1}}{2}$$
よって、\(\frac{-1\pm \sqrt{-3}}{2}\)、\(\sqrt{-3}=\sqrt{3}i\)なので、残りの解は\(x=\frac{-1\pm \sqrt{3}i}{2}\)となります。
すなわち、\(\omega=\frac{-1\pm \sqrt{3}i}{2}\)がωの値となります。
定着用問題(計算)
では、実際にどのような時にωを使うのかについて、ωの復習を兼ねて頻出問題を解いて見ましょう。
ωの問題で一番多いのがωの〇〇乗の値を求めよ。といったものです。
例1):\(\omega^{99}を計算せよ。\)
このような問題はもちろん99回も掛け算をするのではなく、指数法則をうまく用いて処理します。
例1解答:)\((\omega)^{99}=((\omega)^{3})^{33}\)ゆえに、\(1^{33}=1\)だから、答え1。
例2):\(\omega^{5}+\omega^{4}+\omega^{3}の値を求めよ。\)
式の形で問題が与えられる事もありますが、そのほとんどが\(\omega^{3}=1でくくったり\)、\(\omega^{2}+\omega+1=0を用いる\)事で解決します。
例2解答:)\(\omega^{3}(\omega^{2}+\omega+1)\)で、\(x^{2}+x+1=0だったので、1・(0)=0\)
複素数平面とω
ここからは、数2の範囲から数学3の複素数平面でのωについて考えます、
ωの2つの値と、実数1は以下の図のように存在します。
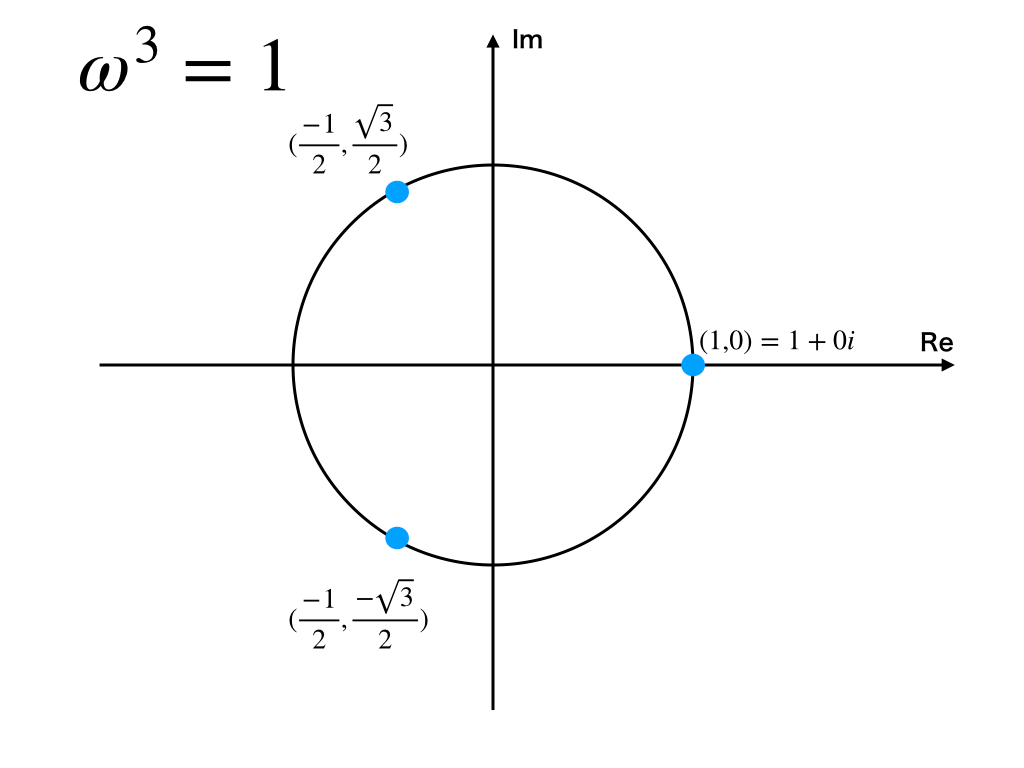
ωを直交形式→極形式へ
まず始めに、これら3つの値を直交形式から極形式に変換しておきます。<参考:「極形式と直交形式の相互変換」>
図より、
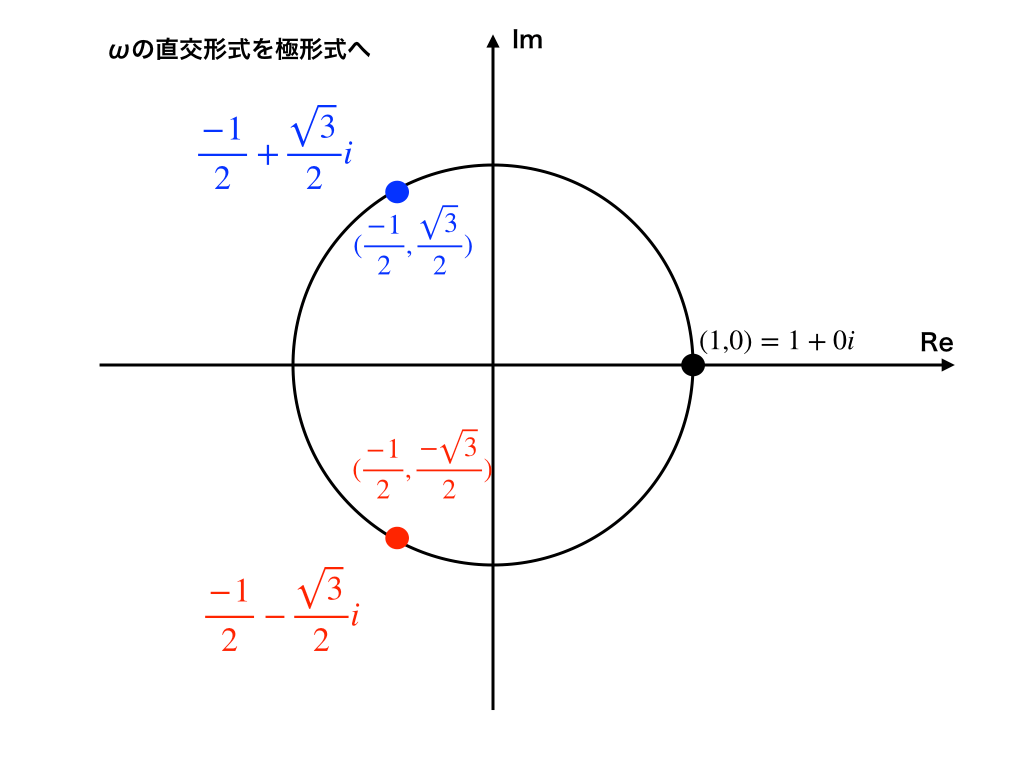
直交形式でのωが3つ表されています。
まず、上図での青色の部分、\(\frac{-1}{2}+\frac{\sqrt{3}}{2}i\)を極形式へ変換すると、
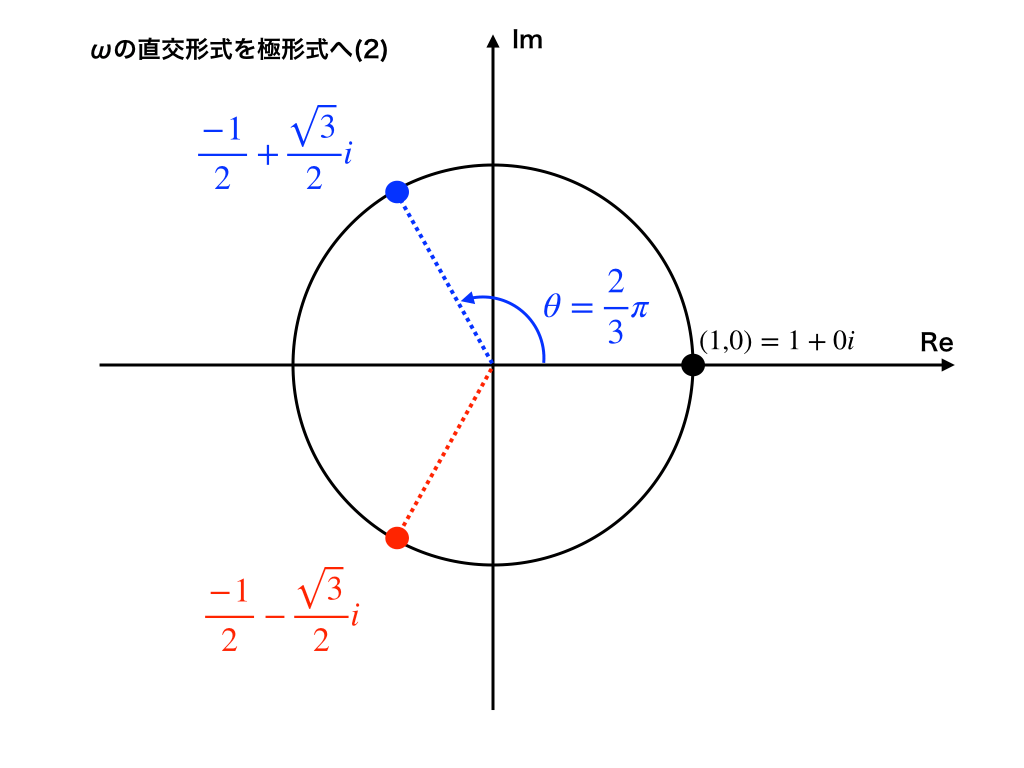
上のようになり、$$\omega=\cos \frac{2}{3}\pi+i\sin \frac{2}{3}\pi$$
次に、赤色の部分を変換すると、
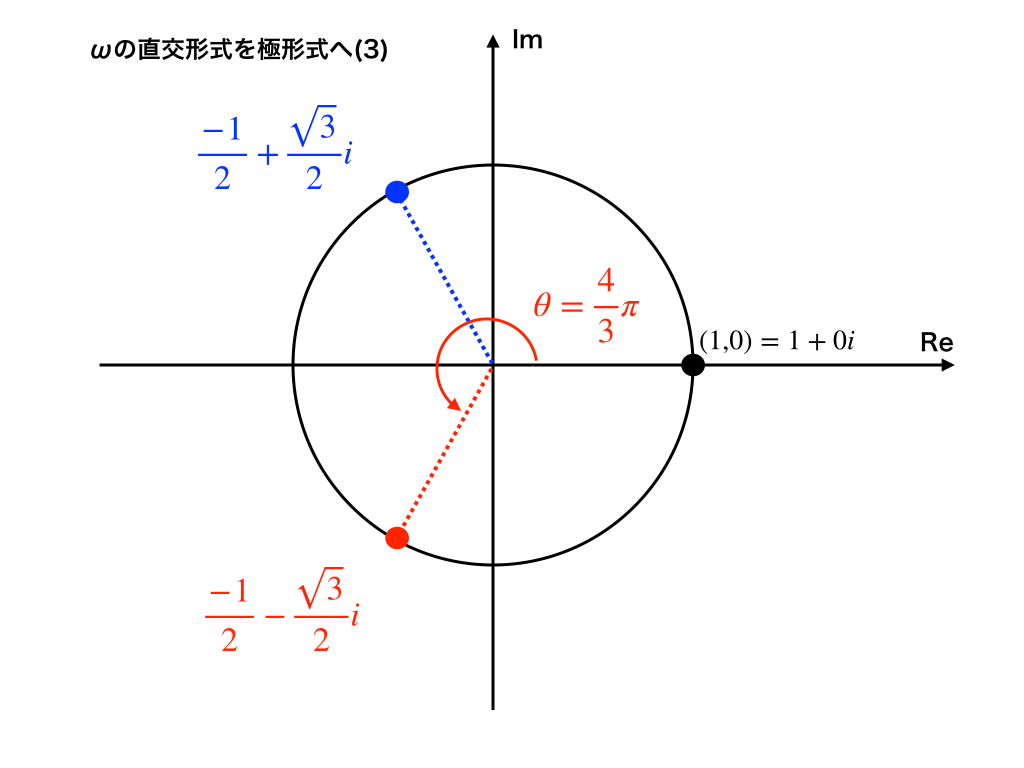
$$\omega=\cos \frac{4}{3}\pi+i\sin \frac{4}{3}\pi$$
最後に残った1+0iも極形式にすると
$$\omega=\cos 0+\sin 0$$
ド・モアブルの定理とω
今度は、ド・モアブルの定理(参考:「ド・モアブルの定理をわかりやすく解説」)を使ってωの二乗を計算して見ます。
\(ω=\frac{-1}{2}+\frac{\sqrt{3}}{2}\)
大きさは変化せず、偏角だけが 2倍されるので
\(ω・ω=\cos \frac{2}{3}\pi \cdot 2 +i\sin \frac{2}{3}\pi \cdot 2\)
\(\omega^{2}=\cos \frac{4}{3}\pi+i\sin \frac{4}{3}\pi \)
この式から、ωの二乗=ωの共役複素数である事が分かります。
同様にωを三乗すると、偏角3倍なので
\(ω^{3}=\cos \frac{2}{3}\pi \cdot 3 +i\sin \frac{2}{3}\pi \cdot 3\)
\(=\cos 2\pi +i\sin 2\pi=1\)
複素平面でωを見る
先ほど、紹介したωの式:\(\omega=\omega^{2}\)や、\(\omega=\bar\omega\)も複素数平面でみるとスッキリ理解しやすくなります。
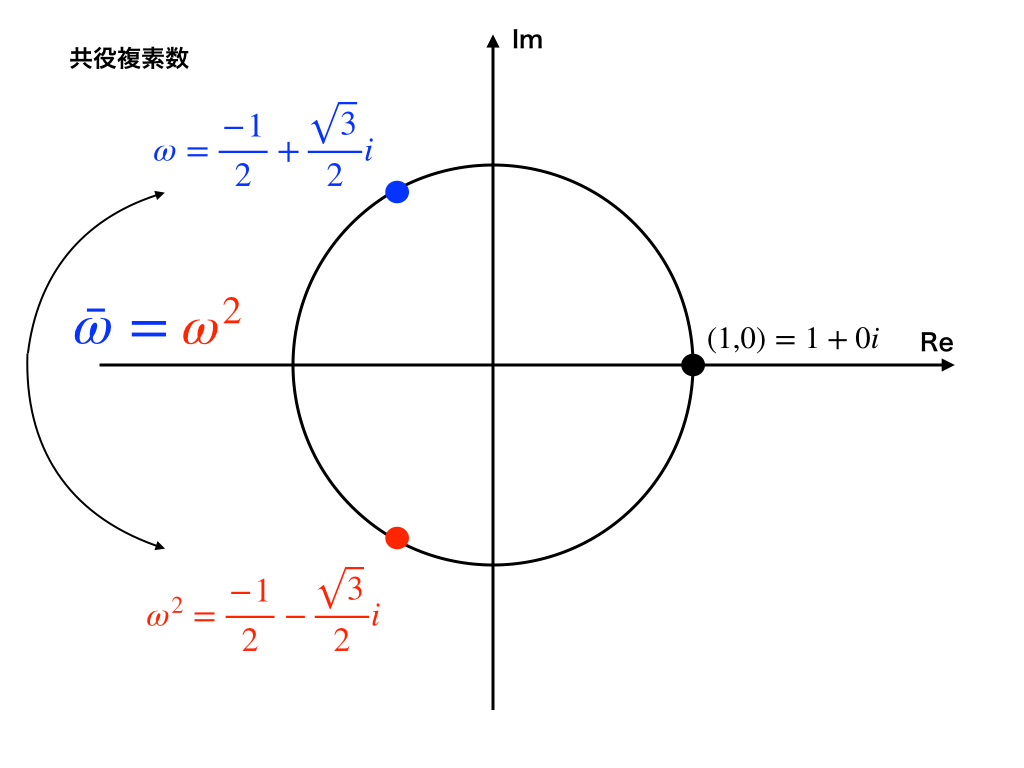
青の\(\bar\omega は\omega^{2}\)と一致していることが分かります。
オメガまとめと関連記事
・三乗すると1になる値(1を除く)をωとおく
・ω関係で、特に頻出の式は\(\bar\omega=\omega^{2},\omega^{2}+\omega+1=0\)
複素数平面シリーズと1のn乗根へ
数学2の複素数の基礎から→数Ⅲの入試レベルまで、「数2から数3の応用レベルまで複素平面を分かりやすく解説」のページに重要な記事をまとめました。
<現在”1のn乗根”についての記事を作成中です>
差がつきやすい分野なので、うまく利用して差をつけましょう!
今回も最後までご覧いただき、有難うございました。
「スマナビング!」では、読者の皆さんのご意見・ご感想、記事のリクエストの募集を行なっています。 ぜひコメント欄までお寄せください。
B!やSNSでシェア、をしていただけると励みになります。
・お問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。

