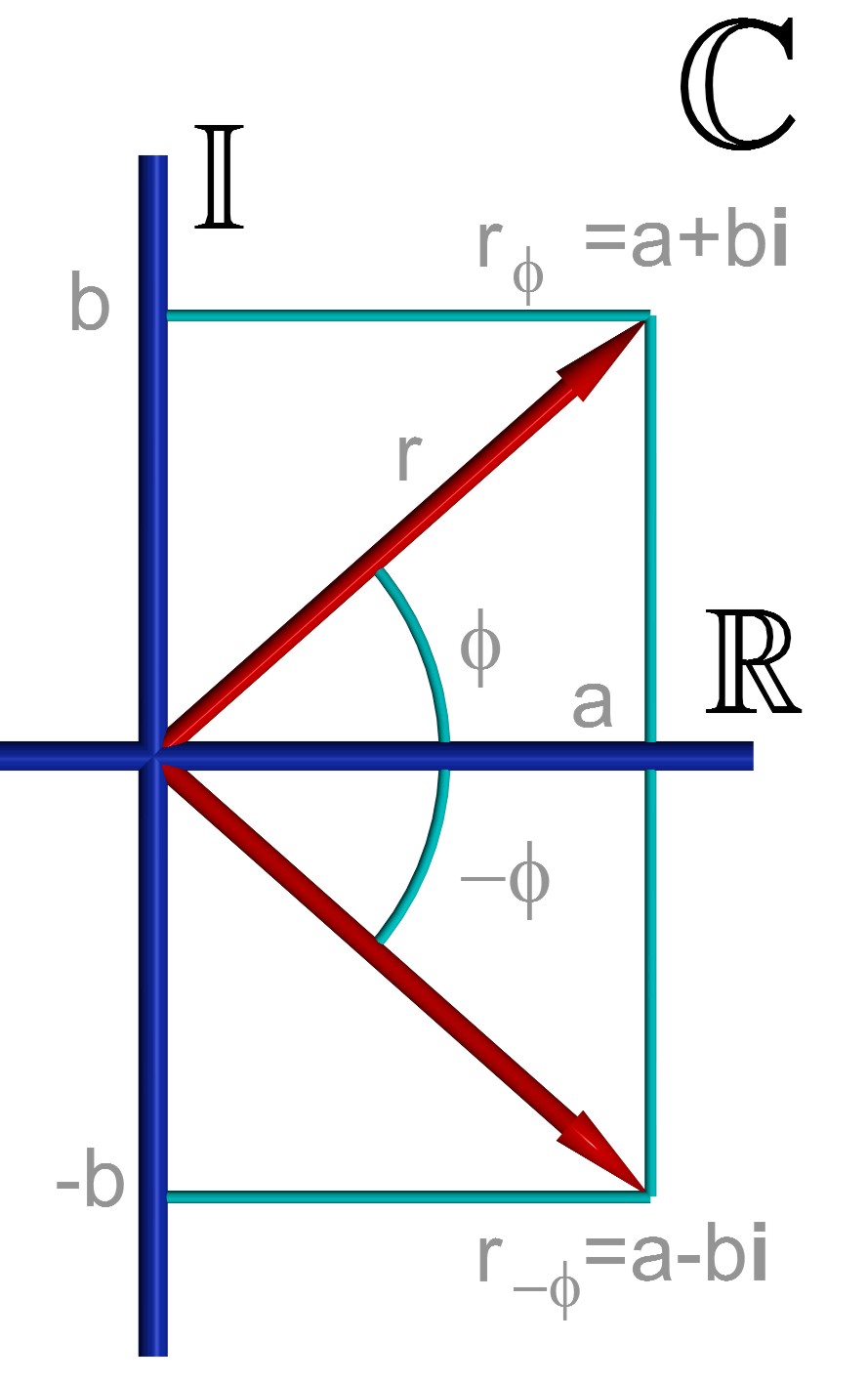
ド・モアブルの定理の証明と三角関数の三倍角の公式への応用
image by Arturo Reina sánchez
今回はド・モアブルの定理を証明し、更にそれを三角関数の二倍角の公式/三倍角の公式の導出に応用して行きます。
ド・モアブルの定理とは?
ド・モアブルの定理は、\(「(cosθ+i sinθ)^{n}=cos(nθ) + i sin(nθ)」\) の形で表せる等式で、
複素数のべき乗の計算をはじめ、複素数平面の問題を解く上で無くてはならないものです。
(例):\(複素数z=(\sqrt{3}+i)\)の6乗を求めよ。
(解き方)
まず複素数\(\sqrt{3}+i\)を極形式であらわす。
$$z=2( cos\frac{\pi}{6} + isin\frac{\pi}{6})$$
ここで、ド・モアブルの定理より
\(z^{6}=2^{6}*( cosπ + isinπ)=64(-1+ 0)\)だから、\(z^{6}=-64 (答)\)
さてこんなに便利な定理はどの様に証明するのでしょうか。
これから解説して行くので、ぜひ自分で証明できるようになるまで、何度も手を動かしながら読んでみて下さい。
今回の証明には数学的帰納法を用います。
以下証明
ド・モアブルの定理の証明
数学的帰納法で証明しますが、途中で加法定理を使います。「<参照>加法定理の証明記事」nを正の整数として
$$(cosθ + i sinθ)^{n}=cos(nθ) + i sin(nθ)を数学的帰納法で証明する。$$
<参考:「数学的帰納法の仕組みと証明の仕方」>
z=cosθ + i sinθと置く。
(1)n=1の時、
(左辺)=cosθ + i sinθ
(右辺)=cosθ + i sinθ となり(左辺)=(右辺)が成り立つ。
(2-1) n=k の時、
$$z^{k}=(cosθ + i sinθ)^{k}=cos(kθ) + i sin(kθ)$$
が成り立つと仮定すると
(2-2)n=k+1の時、
$$z^{k+1}=z^{k}・z=(cosθ + i sinθ)^{k}・(cosθ + i sinθ)$$
$$<ここで(2-1)で、(cosθ + i sinθ)^{k}=cos(kθ)+sin(kθ)と仮定したので>$$
(cos(kθ) + i sin(kθ))・(cosθ + i sinθ)=
(cosθcoskθ + coskθ i sinθ + i sinkθ cosθーsinkθsinθ)
<実部と虚部に分けて>
(cosθcoskθーsinkθsinθ)+ i(sinkθ cosθ + coskθsinθ)=
<ここで三角関数の加法定理を使って>
cos(k+1)θ + isin(k+1)θ
従って、k=n+1の時も成立するので、nが正の整数の時、
$$(cosθ + i sinθ)^{n}=cos(nθ) + i sin(nθ)は常に成り立つ。$$
証明終わり。
この様にして、nが正の整数の時ド・モアブルの定理が成り立つ事が証明出来ました。
ド•モアブルの定理→三倍角の公式
今度は、ド・モアブルの定理を応用して三角関数のn倍角の公式を導いてみましょう。
尚、加法定理を使って2倍角/3倍角を導出している記事は、→「三角関数の公式は覚えない!暗記から導出へ」をご覧下さい。
まず二倍角を導きます。つまりn=2の時です。
2倍角の公式の導出
導き方は、ド・モアブルの定理より、
$$(cosθ + i sinθ)^{2}=cos(2θ) + i sin(2θ)・・・(1)$$
(1)の左辺を展開して、
$$(左辺)=cos ^{2}θーsin ^{2}θ +2i cosθsinθ・・・(2)$$
(1)の右辺と(2)の実部と虚部を比較して
$$(実部) cos ^{2}θーsin ^{2}θ= cos2θ$$
$$(虚部) 2sinθ cosθ=sin2θ$$
この実部は cosの2倍角の公式に、虚部はsinの2倍角の公式になっている事がわかります!
次に三倍角の公式の導出です。
ド・モアブルの定理のn=3の時
$$(cosθ + i sinθ)^{3}=cos(3θ) + i sin(3θ)・・・(3)$$
(左辺)を展開して実部と虚部に整理すると、
<途中式は省略しています>
$$(4 cos ^{3}θー3 cosθ)= cos3θ$$
$$(3sinθー4sin ^{3}θ)=sin3θ$$
これも、同じく3倍角の公式です。
同様に、ド・モアブルの定理を用いることで三角関数の何倍角であろうと導く事ができます(展開する事を考えると実用的ではありませんが...)。
まとめと複素数平面シリーズ一覧へ
複素数平面を利用する事で、「ただ便利」なだけでは無く数学的に色々な興味深い/面白い性質を発見する事が出来ます。
今後も複素数/複素数平面のシリーズを書いて行きます。
お役に立ちましたら、シェア&Twitterのフォローをお願いします。質問、記事リクエスト、その他お問い合わせはコメント欄へお願いします。
お疲れ様でした。

