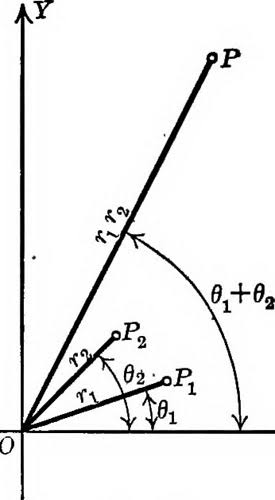
極形式に変換して点を自由に回転伸縮させよう!
前回の「複素数平面とは?基本から極形式・直交形式の意味・変換まで」の続編として、この記事では複素数を直交形式から極形式に変換し、
その掛け算・割り算が複素数平面で回転・拡大/縮小する理由を解説していきます。
複素数の積・商(極形式と回転)
・まずは極形式に変換せよ!(前回解説)
・極形式同士の積の計算法とその証明
・複素数平面上での意味
・極形式同士の商の計算法とその証明
・複素数平面上での意味(割り算編)
前回に引き続き複素数平面の最大の「ウリ」である回転・伸縮について解説していきます。
前回の記事は→「複素数平面の直交形式/座標と極形式/極座標がわかる」
極形式:Z=r(cosθ+isinθ)
\(z_{1}=r_{1}( \cos θ_{1}+i\sin θ_{1}) \)
\(z_{2}=r_{2}(\cos θ_{2}+i\sin θ_{2}) \)
極形式にした複素数同士の積
z1とz2を掛けると
$$z_{1}z_{2}=r_{1}r_{2}(\cos θ_{1}+i\sin θ_{1})( \cos θ_{2}+i\sin θ_{2}) $$となり、これを整理して
\(r_{1}r_{2}\{ ( \cos θ_{1}\cos θ_{2}-\sin θ_{1}\sin θ_{2})+i(\sin θ_{1}\cos θ_{2}+\cos θ_{1}\sin θ_{2})\}\)
ここで、中括弧のなかを加法定理を用いて変形すると
\(r_{1}r_{2}\{ cos( θ_{1}+θ_{2}) +i\sin (θ_{1}+θ_{2})\} \)
複素数平面上での意味
「大きさは掛け算、偏角は足し算」
では、上で計算した複素数どうしの積はどんな意味があるのでしょうか。
\(r_{1}r_{2}\{ cos(θ_{1}+θ_{2}) +i\sin ( θ_{1}+θ_{2})\} \)
の式をよくみると、絶対値は掛け算(r1・r2)偏角argθの部分は足し算になっています。
これを複素数平面上に表すと<図2>の様になります。
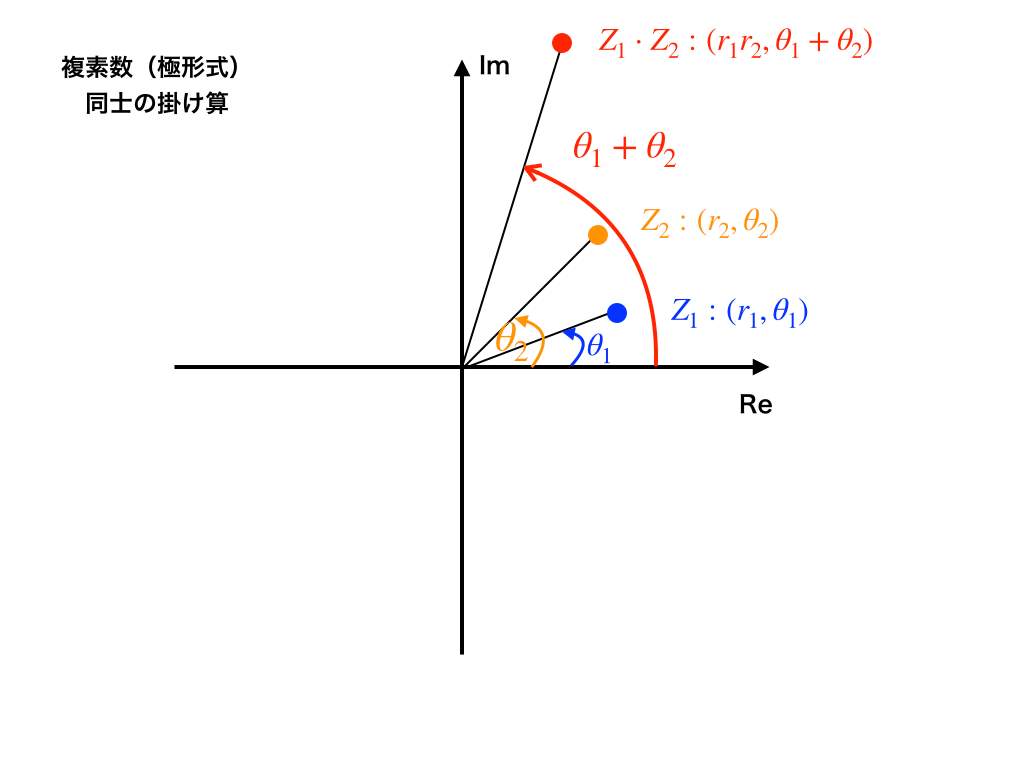
<図2:複素数平面でのかけ算>
これは、かけた極形式の分(r2)だけ絶対値が大きくなり、偏角argθ2の分だけ反時計回りに回転させた事を意味します。
逆に言えば、ある複素数平面上の点Zを”r倍”して”θ分回転”させたければ、
それに対応する複素数の極形式をかければ良い事が分かります。
極形式にした複素数同士の商
次に、極形式での複素数の割り算の意味を見ていきます。
$$\frac {Z_{1}}{Z_{2}}=\frac {r_{1}}{r_{2}}\times \frac {\cos θ _{1}+i\sin θ_{1}}{cosθ _{2}+i\sin θ_{2}}$$
分母分子に(cos θ2ーisin θ2) をかけて

$$\frac {r_{1}}{r_{2}}\frac {( cosθ_{1}+isinθ_{1}) ( \cos θ_{2}-i\sinθ_{2}) }{( \cos θ_{2}+i\sin θ _{2}) ( \cos θ _{2}-i\sin θ_{2}) }これを展開して$$
更に加法定理を分子に用いて
$$\frac {r_{1}}{r_{2}}\frac {cos( \theta _{1}-\theta _{2}) +i\sin (θ_{1}-θ_{2}) }{( cos^{2}\theta _{2}+\sin ^{2}\theta _{2}) }$$
\(\sin ^{2}θ_{2}+\cos ^{2}θ_{2}=1より分母は1\)
(参考:「三角比・三角関数の相互関係と公式」)
したがって$$\frac {z_{1}}{z_{2}}=\frac {r_{1}}{r_{2}}\{ \cos( θ_{1}-θ _{2}) +i\sin ( θ _{1}-θ_{2})\} $$
複素数平面上での意味(割り算編)
「大きさは割り算、偏角は引き算」
複素数平面上での積の意味と同様に、極形式同士の割り算をすると、
<図3>のようにその分絶対値が小さくなり、
偏角argθが小さく(時計回りに回転)する事が分かりました。
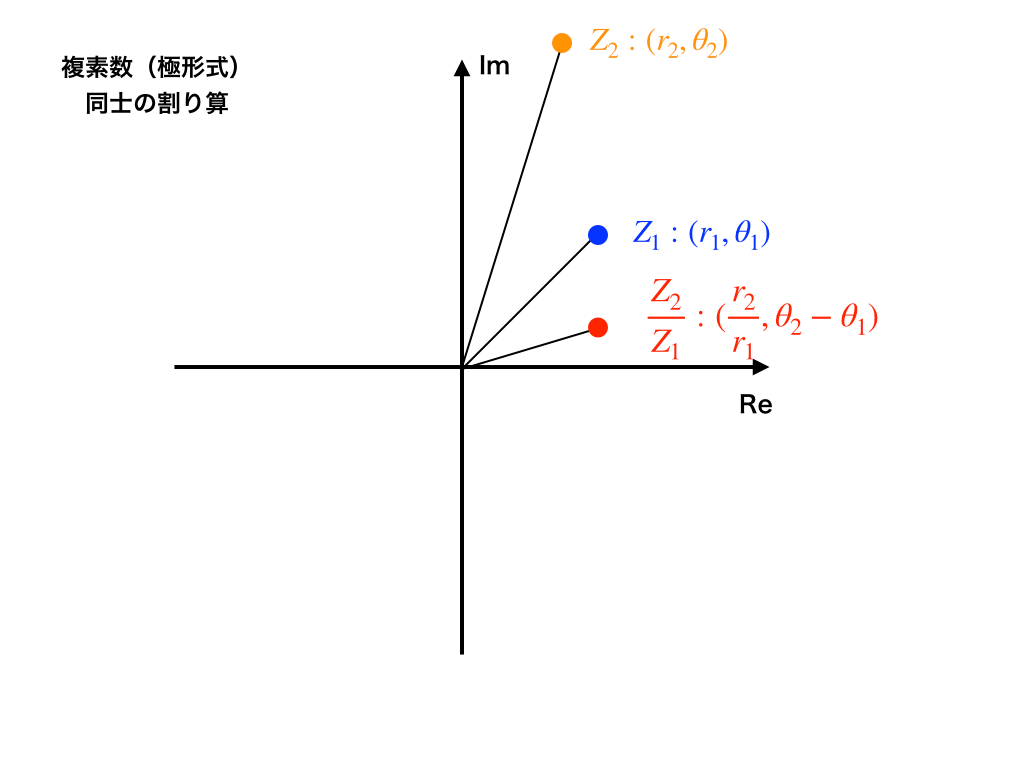
<図3:複素数平面での割り算>
次回と複素平面のまとめ記事へ
複素数平面第3回:「ド・モアブルの定理とその三角関数への応用」
〜複素平面総まとめ記事(NEW!)〜
お疲れ様でした。
今回も最後までご覧いただきまして、有難うございました。
「スマナビング!」では、読者の皆さんのご意見/記事のリクエストなどの募集を行なっています。ぜひコメント欄にお寄せください。
snsでシェアをしていただけると励みになります。
・お問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。
次回は、この複素数の積/商の性質を使って自由自在に点を動かせるようにし、
図形問題への応用へつなげていきます。

