複素数平面上での図形と軌跡(1)
<この記事の内容>:”複素数平面上”での具体的な図形の表し方や、図形と方程式における”軌跡”の分野を複素平面を利用して解く方法などを実例とともに図解しています。
また、一見すると取っ付きにくい\(|z|^{2}=z\bar{z}\)の意味と使い方の習得を目指します。
<これまでの復習>:「複素数平面第一回:0から極座標と直交座標まで」
目次(タップした所へ飛びます)
複素数平面と図形
図形、軌跡に移る前に複素数平面で必須の\(|z|^{2}=z\bar{z}\)の紹介を先にしておきます。
必須知識:絶対値の二乗と共役複素数
以下の式は今後何度も何度も必要になるので、確実に意味(と証明)まで身につけた上で使いこなせるようになる必要があります。
$$|Z|^{2}=Z\bar{Z}$$
ここで\(|Z|\)は複素数Z=a+bi(a,bは実数)としたときの大きさ、\(\bar{Z}\)はZの共役な複素数を意味します。
簡単な証明
Zの絶対値\(|Z|\)というものは、複素平面において以下の図のように、原点からの”距離”を表すと考えることができます。
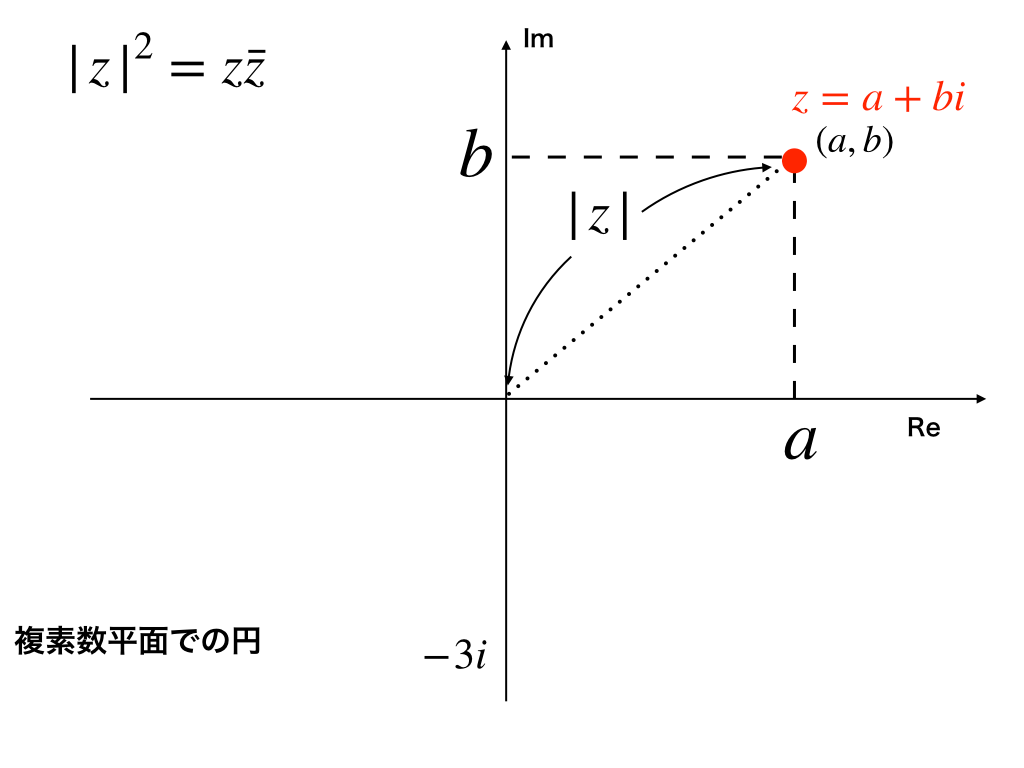
すなわち、三平方の定理より$$(左辺):|z|^{2}=a^{2}+b^{2}$$
さらに、(右辺)は次のように表せるので
$$(右辺):z\bar{z}=(a+bi)(a-bi)$$
$$⇔a^{2}-abi+abi-(-b^{2})⇔a^{2}+b^{2}$$
よって(左辺)=(右辺)が示せました。
円の式とベクトル方程式
次に、ここでは複素数平面での”円”を表す式を紹介します。(図形と方程式(数2)での円の式は→「円の方程式と応用問題」を参照して下さい)
例)\(|z-2|=3\)
上の式が意味することは『zからの距離(絶対値)が常に3である点の集まり』なので、
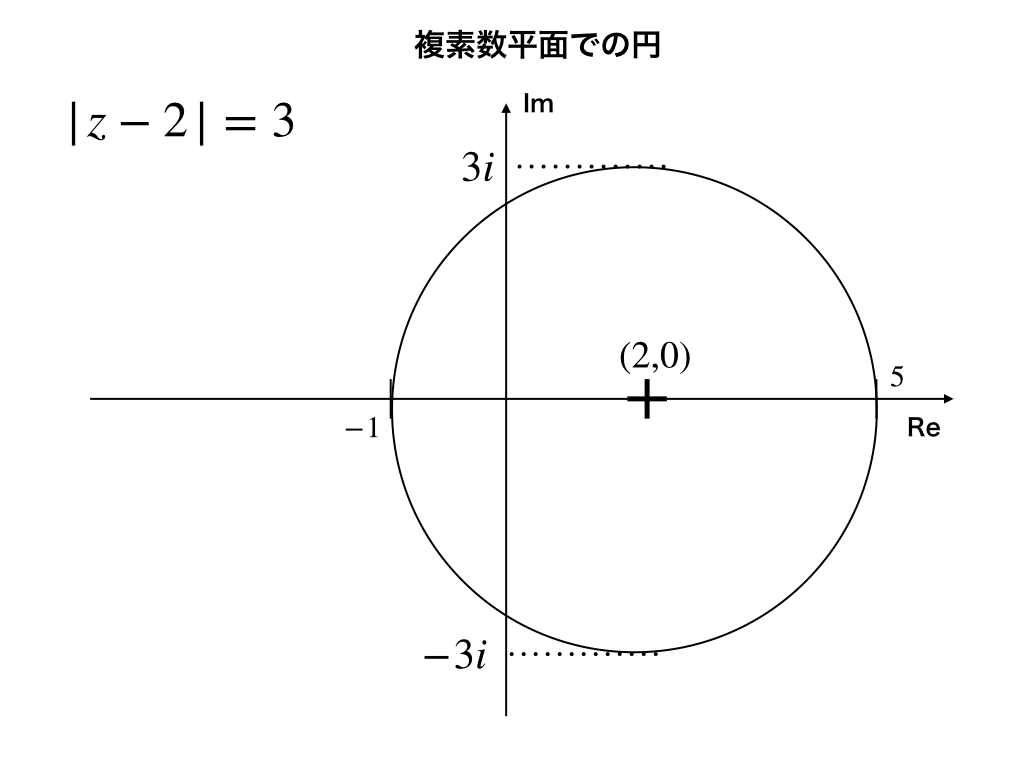
上のような円になります。
これは『円のベクトル方程式』そっくりなことに気がついたでしょうか?

<上のベクトル方程式を図で見ると以下のようになります>
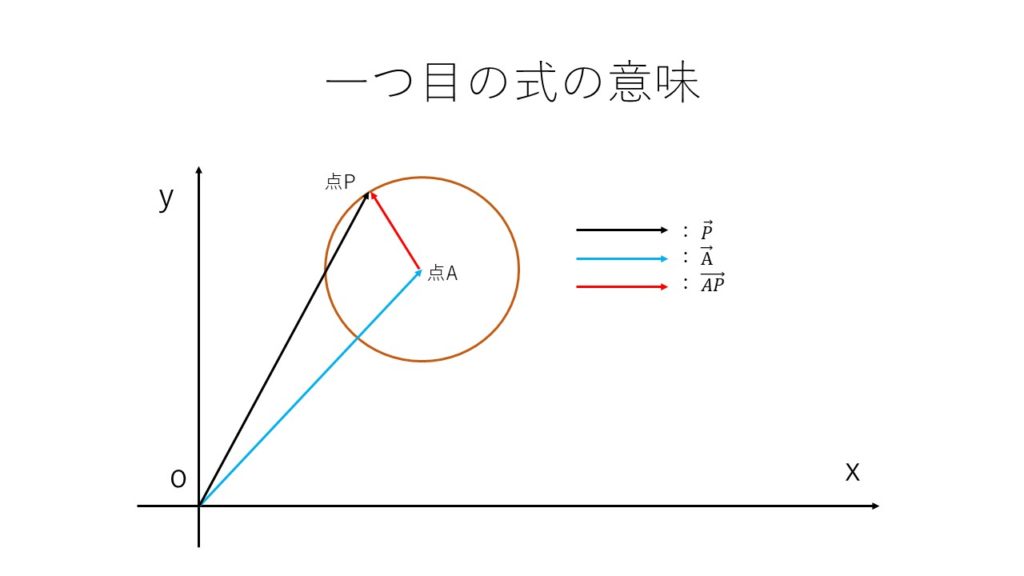
このように”複素数平面”と”ベクトル”の関係はそのほかにもたくさんあり、今後この複素数シリーズで少しずつ紹介と解説をして行きます。
zの条件を満たす軌跡
次に、今回の本題である複素数平面で頻出の”動く点が描く軌跡”の問題を解いて行きます。実際に有名問題を見ながら解法を習得しましょう。
アポロニウスの円
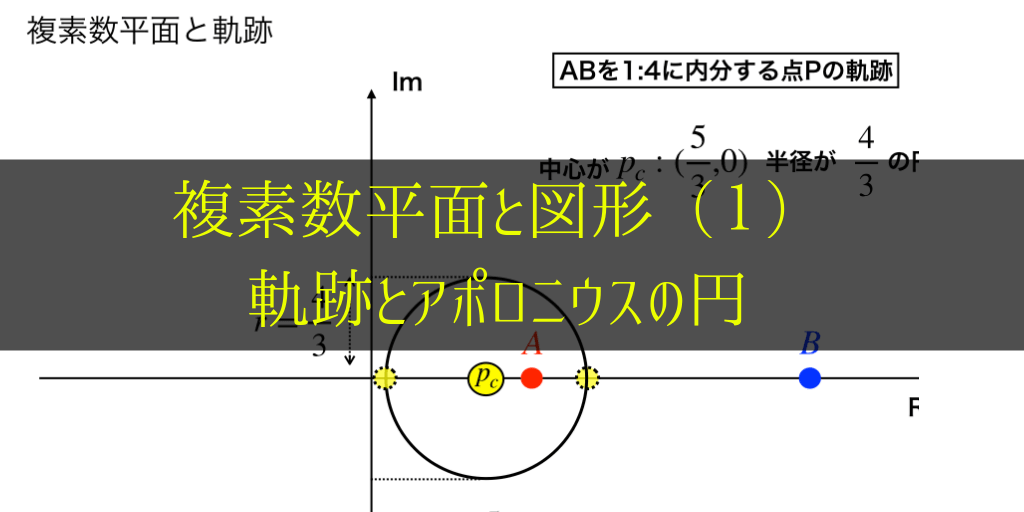
問題:複素数平面上で\(z_{A}=2の点Aとz_{B}=7\)の点Bがある。このABを1:4に内分する点はどのような軌跡を描くか。
内分/外分の復習
図形と方程式/複素数平面の「内分点と外分点の位置と座標の求め方」で詳しく紹介しているので、あいまいな方は先にチェックしておいてください。
解法解説:(推奨)zをそのまま利用する解法
まず、問題文中の内分点を”P”と置くこととします。すると、点Pと点A,Bそれぞれの距離を式にして
$$|AP|:|BP|=1:4$$
内項の積は外項の積だから、4|AP|=|BP|
よって、
4|z-2|=|z-7|
複素数の絶対値は二乗してみる!
絶対値が出てきたらまず二乗、という考え方は非常に大切です。
ここで両辺を二乗して、$$16(z-2)(\overline{z-2})=(z-7)(\overline{z-7})$$
これは、$$16(z-2)(\bar{z}-2)=(z-7)(\bar{z}-7)$$と変形できるので、
これを展開して整理すると\(15z\bar{z}-25z-25\bar{z}+15=0\)となります。
更に両辺を15で割って【\(|z|^{2}=z\bar{z}\)】を利用できるようにしていきます。
$$z\bar{z}-\frac{5}{3}(z+\bar{z})+1=0$$
式変形のコツは\(z\bar{z}\)が出来るように\((z\pm ◯)(\bar{z} \pm △)\)の形を作る事です。
よって、$$(z-\frac{5}{3})(\bar{z}-\frac{5}{3})+1-\frac{25}{9}=0$$
ここで、\(\bar{z}-\frac{5}{3})=\overline{(z-\frac{5}{3})}\)であることに注意すると
$$(z-\frac{5}{3})\overline{(z-\frac{5}{3})}=\frac{16}{9}$$
よって、
\(|z-\frac{5}{3}|^{2}=\frac{16}{9}\)、左辺>0より右辺>0なので、二乗を外すと
\(|z-\frac{5}{3}|=\frac{4}{3} ・・・(※)\)
(※)はまさに先ほど紹介した円の式です。
したがってこの問題の答えは、
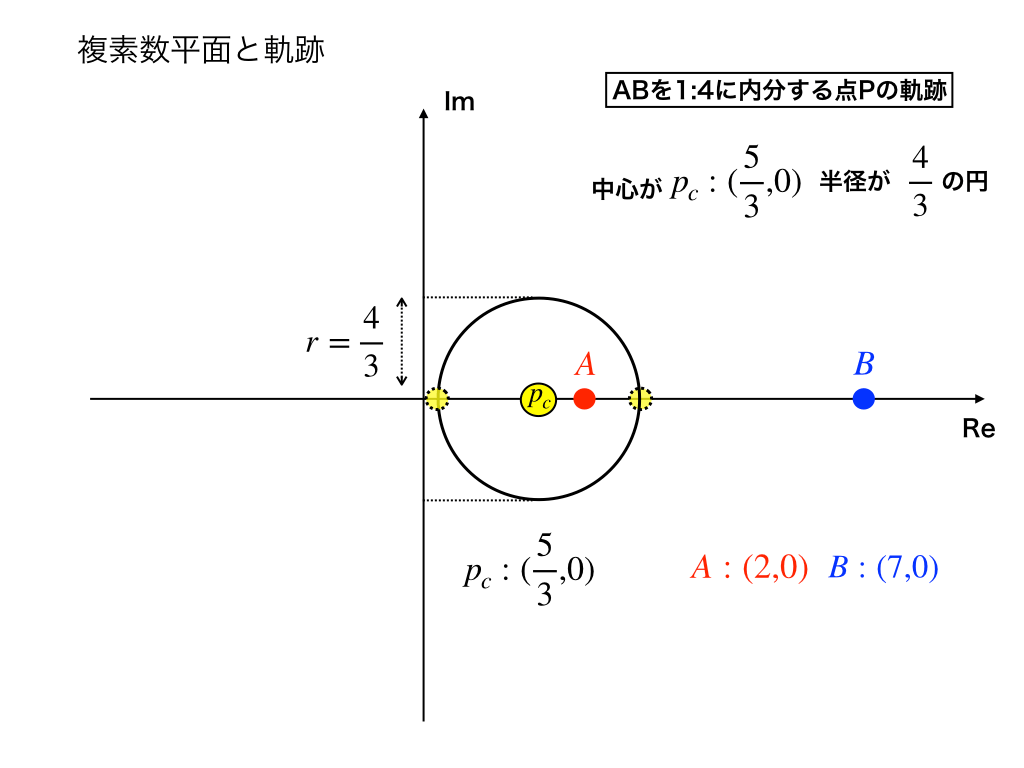
上の図のように、$$中心が(\frac{5}{3},0),半径\frac{4}{3}の円・・・(答え)$$
このような円を【アポロニウスの円】と言い、これ以外の分野でもよく出題されます。
(別解):z=x+y i と置いて計算する解法
上記の\(|z|^{2}=z\bar{z}\)を利用せずに、「z=x+yi(ただしxとyは実数)として式に代入する」方法でもこの問題は解くことが出来ます。
実際にはこちらの方法の方が初めて学ぶ人にとっては分かりやすいのですが、どうしても計算量やミスが増えてしまいがちです。
従って出来るだけ先に紹介した解法を使う事をお勧めします。
複素数平面と図形まとめと続編へ
・アポロニウスの円など、軌跡の問題を複素数“でも”解けるように、できるだけ問題を解く道具を増やしていきましょう!
・関係が深い、ベクトルや図形と方程式の内容を常に振り返りながら次回「(作成中です)複素平面となす角/さまざまな条件」に進みます。
複素数平面シリーズの関係記事一覧
シリーズ第一回:「複素平面が苦手な人へ!〜0から極座標と直交座標まで〜」
複素数平面:第四回(前回)「内分・外分点の位置のみつけ方(複素平面編)」
第五回「今ココです」
複素数平面:第六回(次回)「二直線のなす角や直交条件など」
<参考>:「ベクトルとは?0から予習・復習できる記事総まとめ!」
今回も最後までご覧いただきまして有難うございました。
弊サイト:『スマナビング!』では、読者の皆さんのご意見・ご感想や、をコメント欄にて募集しています。
また、お役に立ちましたらB!や、SNS等でシェアをしていただけると大変励みになります!
・その他のご依頼等に関しましては、お問い合わせページからご連絡下さい。

