二次関数で苦手な単元No.1!最大・最小問題
数学1の二次関数の分野でも、とにかく嫌われやすい「最大値・最小値」の分野。
確かに、定義域(xの範囲)が動いたり、グラフそのものが動いたり、と場合分けがややこしく一つの大きな壁であることは確かです。
この記事を見てくださっているあなたも、この壁にあたっているのではないでしょうか?
この記事では、定義域/グラフが動いた際の二次関数の最小値/最大値を求める問題の考え方をイラストと、帯のイメージを使ってわかりやすく解説していきます。
目次(タップした所へ飛びます)
二次関数のグラフの最大値最小値
全ての初めに、「定義域」と「値域」の説明から行います。
定義域と値域とは
今後何百回も目にするであろう単語です。なるべく簡単に紹介すると、
定義域とは、関数(この記事では2次関数f(x)=ax2+bx+c)の”x”の範囲のことを言います。
そして、二次関数をグラフで表した時、y=ax2+bx+c のxの値に対応してyの値が求まります。
例えば、x=0を代入するとy=cとなり、x=1を代入するとy=a+b+c となりますね。
この定義域に対して求まるyのことを値域と呼びます。
つまり、定義域○〜△のときの値域を求めよ。と言われたら、そのxの区間のyを答えれば良いのです。
何と無くイメージはつかめましたか?厳密な説明ではないですが、今の段階ではこのくらいの理解で十分です。
二次関数のグラフの復習
次に二次関数の最大・最小問題を解く際に欠かせないグラフを少しだけ復習しておきましょう。
y=ax2+bx+c のグラフでは、a>0の時下に凸となり
、軸はx=-b/2a、頂点の座標は(-b/2a , c-b2/4a)と表すことができます。
(詳しくは、「二次関数のグラフと解の存在範囲」の記事を参照してください)
特に、最大値/最小値を求める問題では「軸」が最重要なので常に注意するようにしましょう。
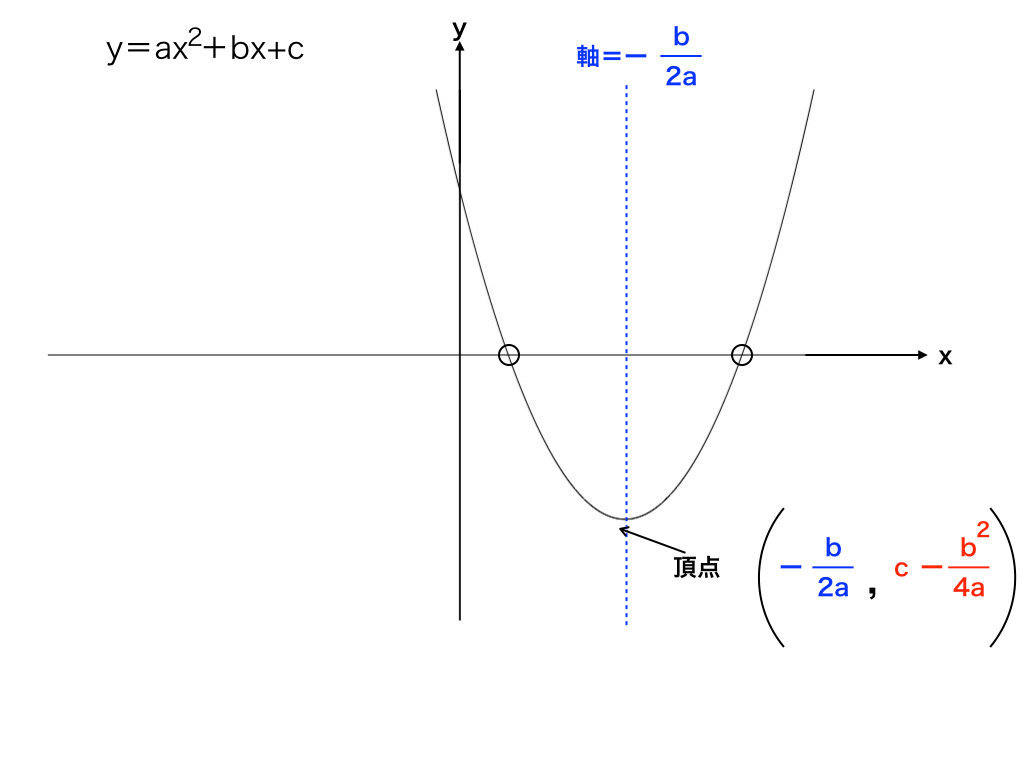
<二次関数のグラフ例>
定義域が動くタイプの二次関数の値域の問題
ここからは、定義域;すなわちxの範囲が移動するタイプの問題の解き方を解説していきます。
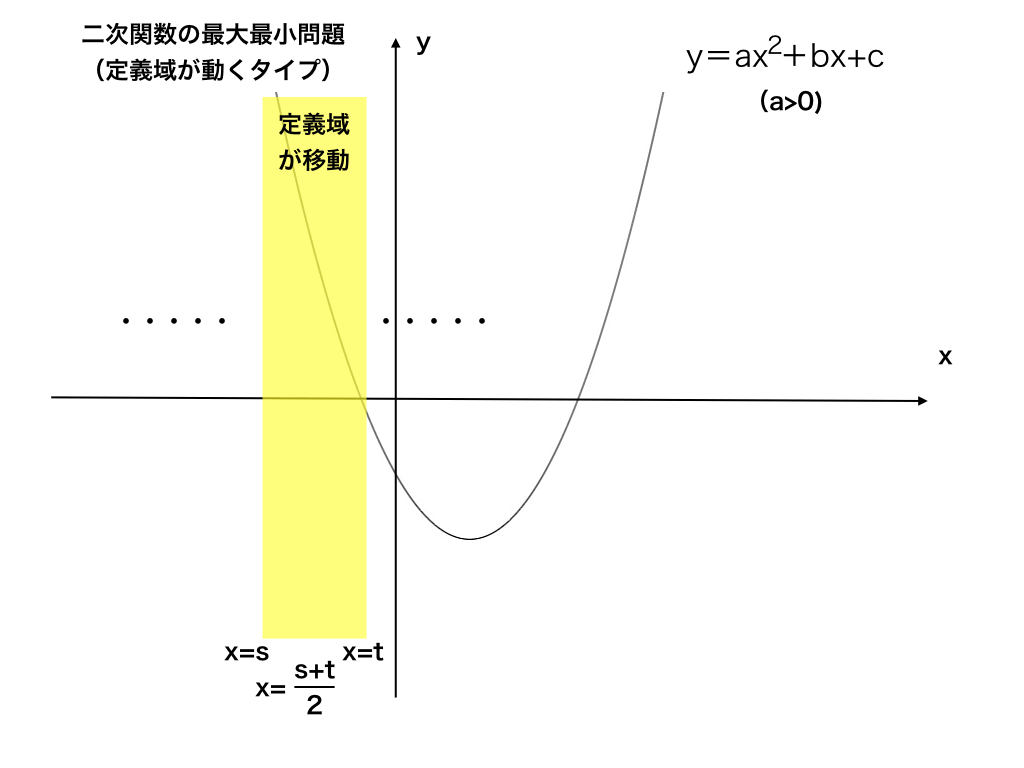
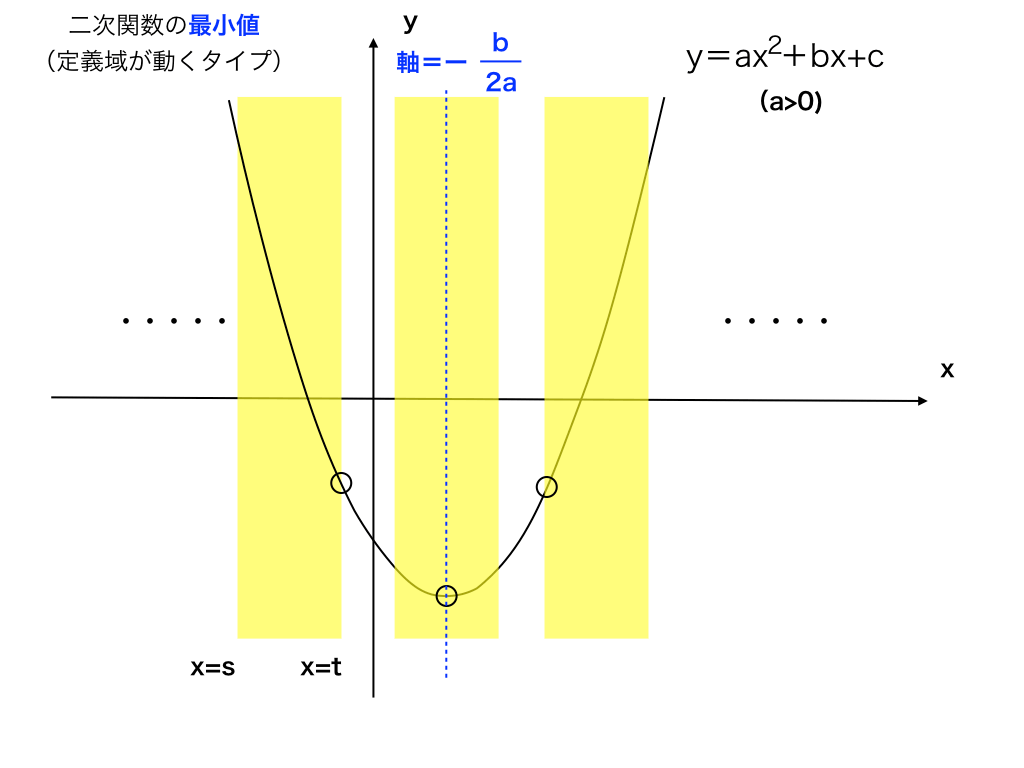
では、上の図のように、下に凸の二次関数のグラフがあるとき、x軸に並行なx=sからx=tまでの”帯”(図中では黄色で示している部分です=「定義域」)が左右に動く場合に、二次関数の最大値、最小値はどのような値をとるかを見てみましょう。
値域の最大値
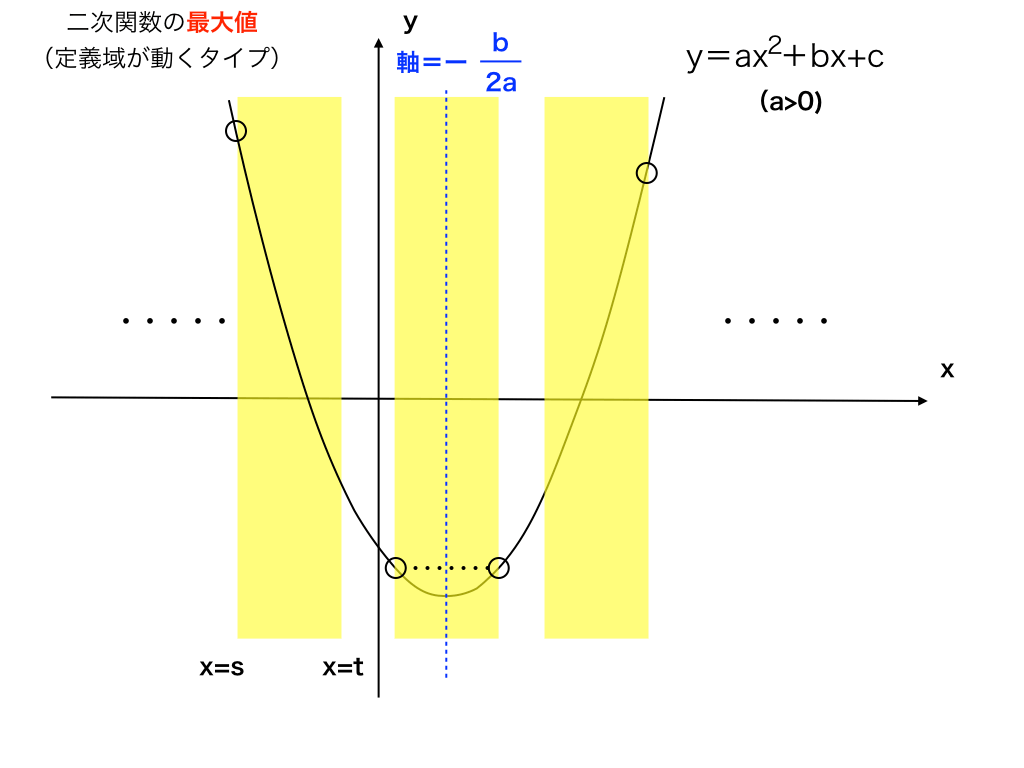
最大値は、下の図のように大きく3種類(*下の三通りのうち3番目については、1or2番目と合わせて回答することが多いです)に場合分けする必要があります。
つまり、x=s+t/2(=黄色(定義域)の帯のちょうど真ん中でy軸に並行な直線)よりも軸の値が大きいか、小さいか、同じ値をとるかです。
(1)x=s+t/2の値が軸よりも小さいならば、図の一番左の”帯”の状況となり、最大値はx=sのときのyとなります。
(2)x=s+t/2の値が軸よりも大きいとき、一番右の帯のように、x=tで最大値をとることになります。
(3)最後に。x=s+t/2 と 軸 が同じとき、(ちょうど真ん中の帯)に注目すると、最大値がx=s ,tの2箇所で同じ値を取ります。
値域の最小値
次の最小値は、
・軸の値よりも帯の右端(x=t)が左にある場合と
・軸の左端(x=s)が右側にある場合、更に、
・軸が帯の中(s<軸<t)にあるときの3通りに場合分けします。
軸<sのとき
定義域の小さい方の端(x=s)よりも軸の値が小さい場合、
最小値はx=sでのy座標になります。(図の一番右の帯)
s<軸<tのとき
軸が帯の中にあるとき(図中の真ん中の帯)、その最小値は軸でのyの値(つまり、二次関数のグラフの頂点のy座標)となります。
t<軸のとき
軸の値が”帯”の左端よりも更に大きい場合(図の一番左の”帯”)、最小値は、x=tのときのy座標になります。
グラフそのものが動くタイプの値域
次に『定義域』ではなく『二次関数のグラフそのものが動く』タイプの最大最小を求めていきます。
この場合、定義域は固定(図中の赤い帯の部分)されてます。

値域の最大値
グラフが動くときも、その値域の最大値は軸と”帯の中心”の位置関係で場合分けを行います。
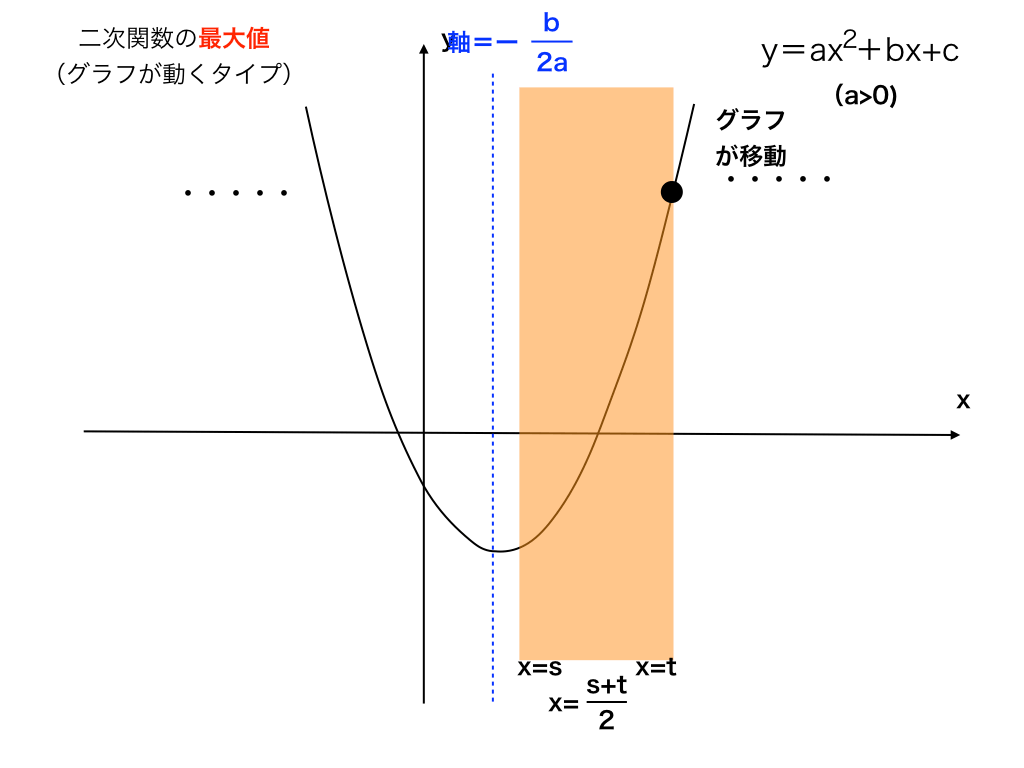
軸<s+t/2
まず、軸が帯の中心(x=s+t/2)よりも小さい場合、最大値はx=tの時のyの値になります。
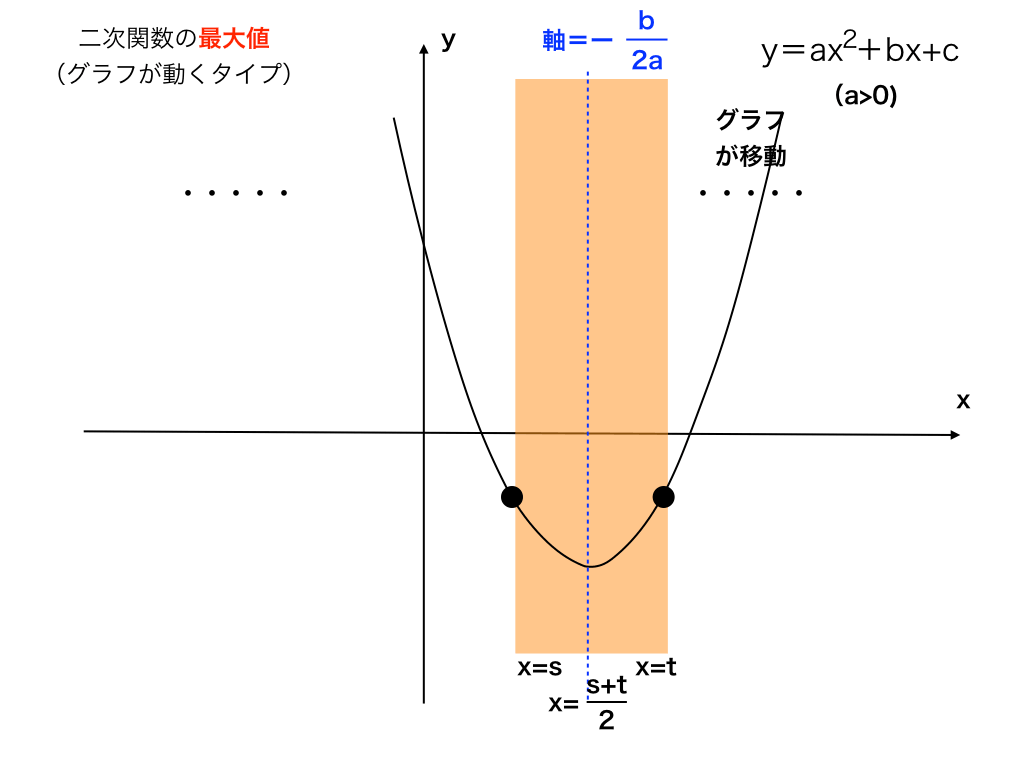
軸=s+t/2
軸と帯の中心のx座標が同じ場合、最大値はx=s,tの時のyの値(以下の図のように最大値は同じで、個数が2つ)になります。
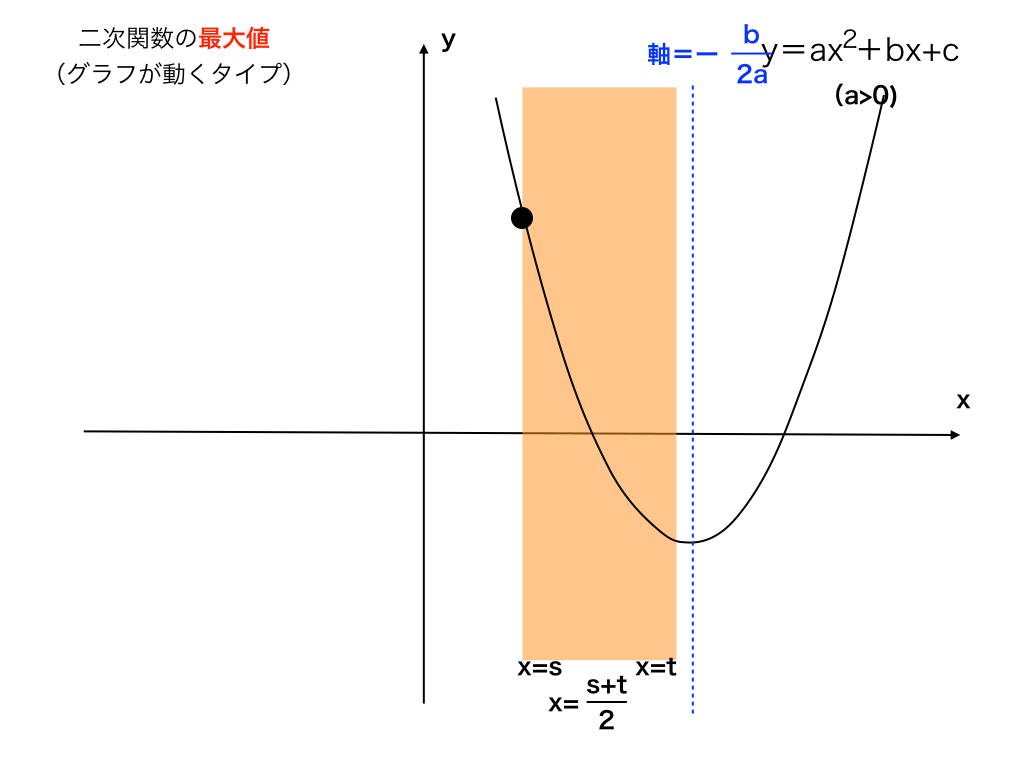
軸>s+t/2
次に、軸が帯の中心よりも大きい場合、最大値はx=sの時のyの値になります。
値域の最小値
定義域ではなくグラフそのものが動くときも、基本的な考え方は変わりません。
つまり、軸の値と定義域の両端との大小・または定義域中に軸があるかに注目して場合分けを行います。
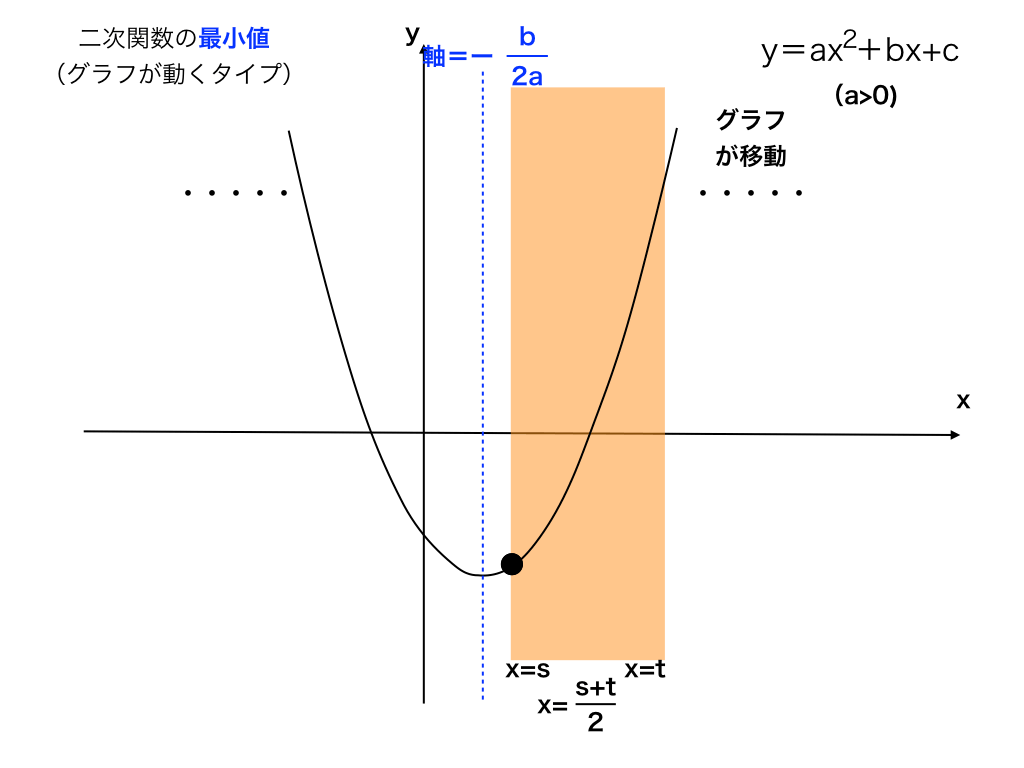
軸<s
定義域の小さい方の端(x=s)よりも軸の値が小さい場合、
最小値はx=sでのy座標になります。
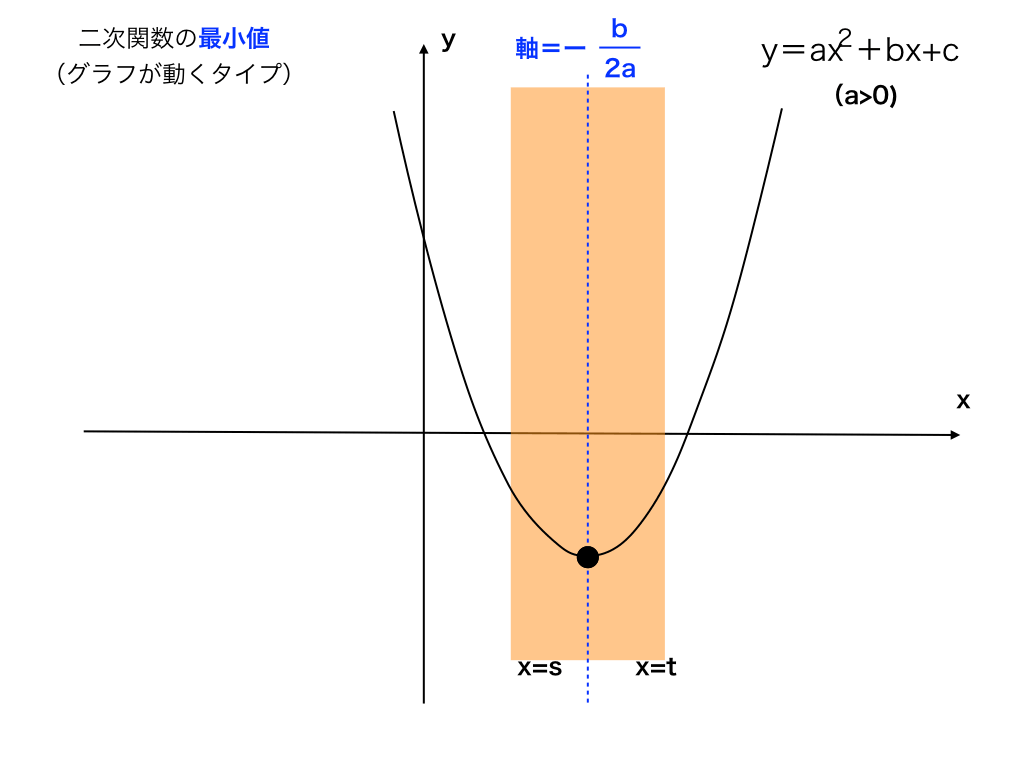
s<軸<t
二次関数のグラフの軸が帯s<x<tの中にあるとき、最小値は頂点でのyの値になります。
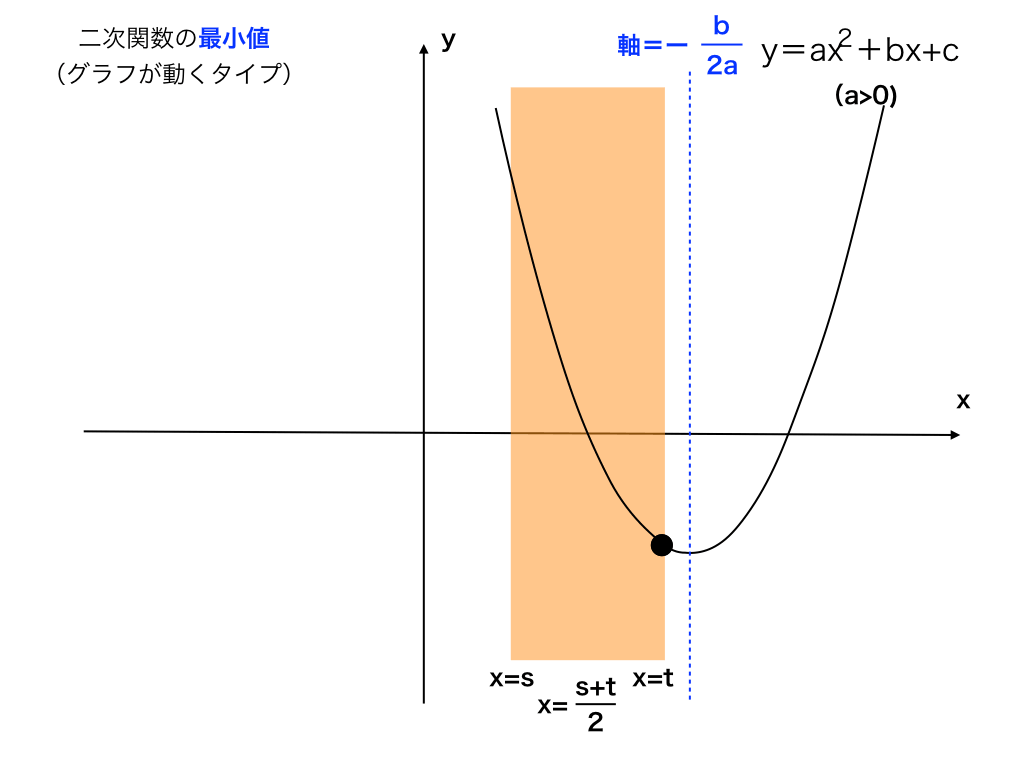
軸>t
定義域の大きい方の端(x=t)よりも軸の値が大きい場合、
最小値はx=tでのy座標になります。
二次関数の関連記事
このように、グラフが動くときも、定義域が動くときも、ほとんど同じ考え方で最大値・最小値を求めることができました。(軸と定義域の両端、および、軸と定義域の中心の値の位置で場合分け)
この記事では、下に凸のグラフで解説しましたが、上に凸のグラフの場合や最大値(or最小値)を場合分けした上で、そのグラフを描かせる問題もよく出題されます。
問題集などで必ず載っているので類題を探して練習してみてください。
関連記事と2変数関数の最小問題へ
今回も最後までご覧いただきまして、有難うございました。
当サイト「スマホで学ぶサイト、スマナビング!」は日々改善、記事の追加、更新を行なっています。
・リクエストや質問がございましたらコメント欄にお寄せください。
・snsでいいね!やシェア、Twitterのフォローをしていただけると助かります。

