
統計学超入門講座
<このまとめ記事の内容>:統計学を学びたい方を対象に、高校レベルの”データの分析”から本格的な統計、ベイズ統計まで独学で習得するために役立つ解説記事をまとています。
※:記事が増えてきたのでまとめページを作成しました。コンテンツは随時追加していくので、作成中の項目(推計・ベイズ統計など)は少々お待ちください。
目次(タップした所へ飛びます)
統計学導入~記述統計・データの分析
統計学・データの分析を学び始めるにあたって、その学習の流れや全体像などを
・「統計学入門:イントロダクション」でまず紹介しています。
(準備)場合の数・確率
上のイントロダクションでも解説したように、確率の考え方は統計学のベースになります。
高校範囲での重要な項目は
・「場合の数・確率の解説記事まとめ」を参考にしてください。
代表値・箱ひげ図
まずはじめのはじめに学ぶのは、高校数学1で扱われている「代表値と箱ひげ図の書き方」です。
これからの統計の第一歩で、身近な平均値・中央値、四分位数などを学びます。
これらの知識があるだけでも、ニュースなどで登場する『グラフ』の意味を正確に理解しやすくなります。
分散・標準偏差
ここでは、データの散らばりを意味する分散や標準偏差の求め方、偏差平方和(下の記事で詳しく解説しています。)を分散とする意味などを
・「データの分析:分散・標準偏差」でまとめています。
共分散・相関係数
2変数の間での相関関係を表す『相関係数』や分散・共分散行列でも登場する共分散について
・「データ分析:共分散と相関係数の意味と求め方」で紹介しています。
データの変量変換
ここでは、データを別の式に置き換えた時について「データの変量変換と標準化」にて詳しく解説しています。
期待値/分散の演算子と性質
この辺りから、高校で扱う統計的な推測を超えて大学教養レベルの統計学へと進んで行きます。
その橋渡しとして、「期待値E(X)/分散V(X)の意味とそれぞれの性質」を読んで行きましょう。
確率分布まとめ
確率分布は多くの種類があり、これらを理解し身に付けることが、のちの推測統計・検定でとても大切になってきます。
確率分布と確率変数イントロダクション
「確率分布と確率変数/密度・質量関数の意味」では、そもそも確率分布/変数とは何か?という解説から始めます。
よくあるつまずきポイント(連続型の確率においてある値をとる確率が0である理由など)も丁寧にイラストで解説しました。
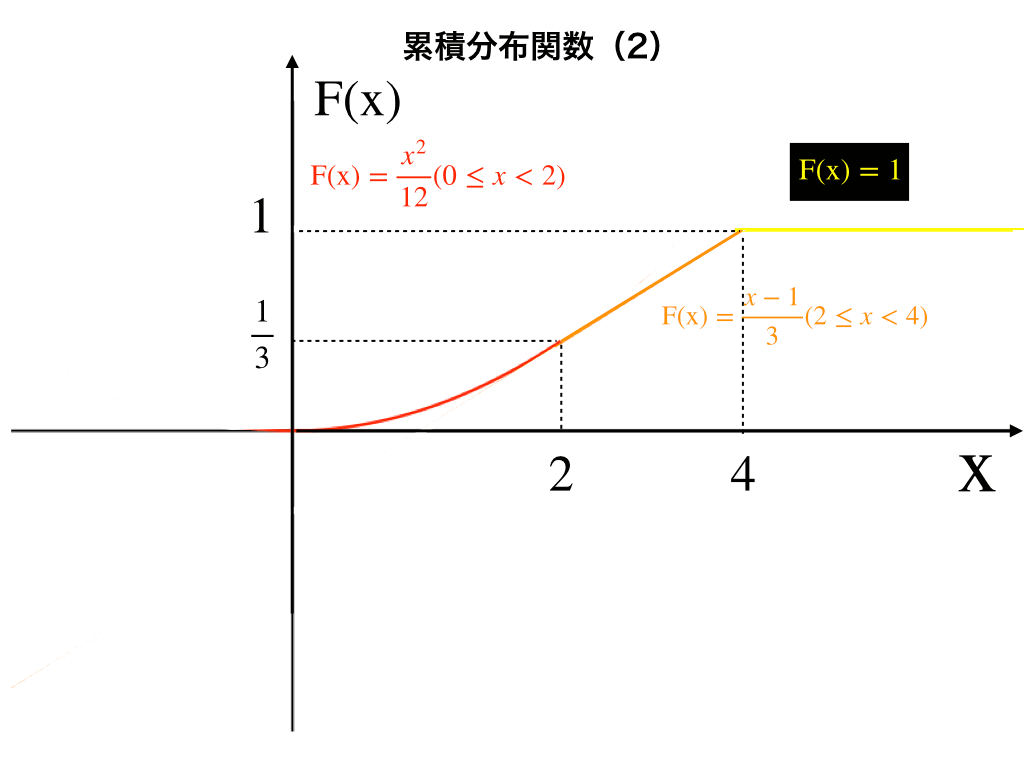
累積分布関数とは
「累積分布関数と確率密度/質量関数」の関係を具体的な問題とグラフを使って解説しています。
モーメント母関数とその意味
積率(モーメント)母関数と呼ばれ、”0”や平均値周りのn次のモーメントを”生み出す”関数について解説しています。
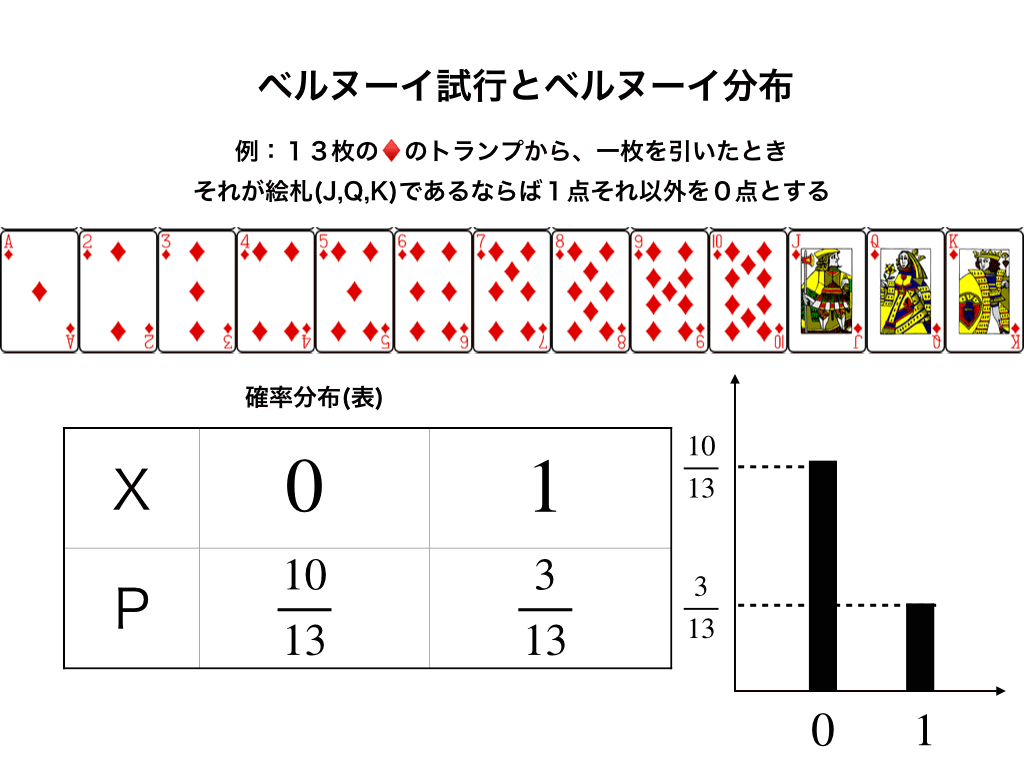
ベルヌーイ分布と二項分布
上の2記事で基礎の基礎を学んだら、「ベルヌーイ試行と分布、そして二項分布へ」で最も基本的な確率分布であるベルヌーイ・二項分布を見ていきます。
正規分布・標準正規分布
二項分布から発展し、確率分布の中でも最重要である『正規分布』および、『標準正規分布』について学びます。
正規分布表の読み方やエクセルでの作成法なども紹介します。
ポアソン分布とは
「ポアソン分布とは?質量関数・母関数・期待値等」の解説と導出をしている記事を追加しました。
推計統計学
ここまではデータを整理したり、どの様な確率分布があるかを学んできました。
ここから先の推計統計学では、母集団からサンプリングした標本をもとにして、母数を推定する方法を見ていきます。
点推定
点推定第一回として、不偏推定についてみていきます。
「(作成中です):最尤推定・尤度関数」
区間推定
点推定と異なり、区間(幅)で母数を推定します。
※:ここでの”区間”は、不偏分散の記事でも解説しているのですが、「『母数が変数』であるということでは無く」例えば、「1000回標本を取り出したら990回は母数が標本の中に入っている」(99%信頼区間)という意味です。
検定とは
例えば、上で推測した統計量が妥当なものなのか否かといったことを調べることを『検定』といいます。
ベイズ統計学と頻度主義
ここまで学んできた分野は「頻度論」(客観確率を重視)というものをベースにして来ました。
一方でトーマス・ベイズに始まる”ベイズ統計”は長年『異端』のような扱いを受けていましたが、今日の計算機(コンピュータ)の演算能力の進化や、AIに関連する技術の進化によって俄然注目を集め、実際にあるゆる場面で使用されることになりました。
条件付き確率とベイズの定理の準備
「(作成中)ベイズの定理」
モチベーション維持と到達度チェックに使える資格・検定
独学や(スクールなどに通っていても)、難解な統計学・数学の理論に向き合っているとモチベーションが低下したり、どの程度知識が定着しているか不安になったりするものです。
ここではそんなときに役立つ、上の記事で学んだ内容をもとに受けることができ”歴史・実績”がある”良質な検定試験”について紹介します。
実務と重複するものも多く、グレードを少しずつあげて取得することで自信にもつながるので是非挑戦してみてください。
統計検定
英語検定や漢字検定などに比べるとやや知名度が低い統計検定ですが、上位の級ではかなり実践的な内容を問われるなど、ぜひ取り組んでおきたい検定です
各級の目安と内容
現在統計検定は4級・3級・2級・準1級・1級の5段階のレベルに分かれています。
過去問などの概要は公式のHPに乗っているのでそちらを参照していただければと思います。
4級はかなりやさしい内容なので、3級,できれば2級からチャレンジしてみることをお勧めしています。
数学検定
いわゆる数検は、統計検定ほど確率統計の分野から出題される問題数は多くありません。
ただし、それを支える”高校数学〜大学教養レベル”くらいまでの習熟度を、”まとめてチェックできる”優れた資格試験と言えます。
数検の概要と各級の目安
数検は(算数検定という子ども向けを除くと)5〜1級までの7つのレベルがあります。
準1級が高校3年程度(数学Ⅲまで)
一級が大学教養〜の出題範囲となっており、このサイトの記事で解説している内容で準一級+αはクリアできるはずです。
数検準一級→一級を目指す
ただし、本格的な確率・統計や線形代数は一級でのみ出題されるので、一級を目指したいところです。
(解析分野では、若干難易度の高い微分方程式などが出題されますが勉強しておいて損はないです)
統計学とその関連分野
統計学はそれ単体で存在しているわけではありません。
下ででまとめている【線形代数】や【微分積分学】など、様々な分野の知識が必要とされる学問です。
また、『機械学習や深層学習のために必要な記事を集めたページ』にも、統計学とオーバーラップした範囲が多いので、
以下の3つのまとめページも同時にブックマークなどをして、利用していただけるとより一層理解がはかどるかと思います。
関連分野(機械学習/線形代数/微積分)の記事へ
まだまだ追加していきますが、これらの記事を通して、統計学・線型代数学・解析学等の理解の一助となれば幸いです。

