
統計学入門(4):正規分布と標準正規分布
<この記事の内容>:統計学において最重要の確率分布(連続型)である、
・正規分布と
・標準正規分布について、
前回「ベルヌーイ分布と二項分布」との関係を紹介しながら、性質や証明などを解説していきます。
目次(タップした所へ飛びます)
正規分布とは
正規分布は、いわゆる『つりがね型』の連続確率分布で、数多くの現象がこの分布に従う統計学において最も重要な確率分布です。
二項分布との関係
二項分布においてn、すなわち”ベルヌーイ試行の回数”が十分に大きいとき、確率分布は今回扱う正規分布にどんどんと近づいていきます。
さらにこの正規分布を"標準化"する事で、標準正規分布(→下の項で扱います)と言う非常に便利な確率分布と、(標準)正規分布表を用いることが可能になります。
正規分布と中心極限定理
また、中心極限定理により「どの様な」確率分布でも、試行を繰り返すことで正規分布に従うことがわかっています。
この『どのような確率分布でも』というところが最大のポイントです。
(※詳細と証明は「(作成中です)中心極限定理」で行います。)
これにより、正規・標準正規分布は推測統計を始めあらゆる分野で利用されることとなりました。
正規分布の公式
\(\mathrm{N}(μ、σ^{2})\)で表される正規分布の分布曲線(密度関数)、期待値、分散をまとめておきます。
正規分布曲線は$$f(x)=\frac{1}{\sqrt{2\sigma}}e^{\frac{-(x-\mu)^{2}}{2\sigma^{2}}}$$
期待値と分散
期待値:\(\mathrm{E[X]=\mu}\)
分散;\(\mathrm{V[X]=\sigma^{2}}\)
標準正規分布:正規分布の標準化
正規分布は様々な局面で現れ便利なものですが、正規分布を『標準化』することで【標準正規分布】に変換することが可能です。
この標準化によって、正規分布表を利用し簡単にその面積=確率を求めることができるようになります。
標準正規分布とは
\(\mathrm{N(μ,σ^{2})}\)で表される正規分布を、平均(期待値)が0;分散を1にしたものを標準正規分布と呼びます。
つまり「変量変換とデータの標準化」と「確率変数の標準化」で解説している『標準化』を正規分布に対して行うことで、標準正規分布を得ることができます。
標準化を行う方法は、
$$Z=\frac{x-\mu}{\sigma}$$
として、変数をxからzに変換すれば良いです。
正規分布曲線の積分と確率
さて、標準化した正規分布曲線は以下の様な(釣り鐘型)であり、曲線は
$$f(x)=\frac{1}{\sqrt{2\pi}}e^{\frac{-x^{2}}{2}}$$で表すことができます。
このように底がネイピア数e(参照:『ネイピア数とは?何とためにあるのか、意味と歴史を徹底解説』)で、指数部分が複雑な式を扱うときは、“exp()”:エクスポネンシャルを使います。
例:\(\mathrm{e^{\sin\theta}}であれば,\mathrm{exp(\sin\theta)}\)のように表記します。
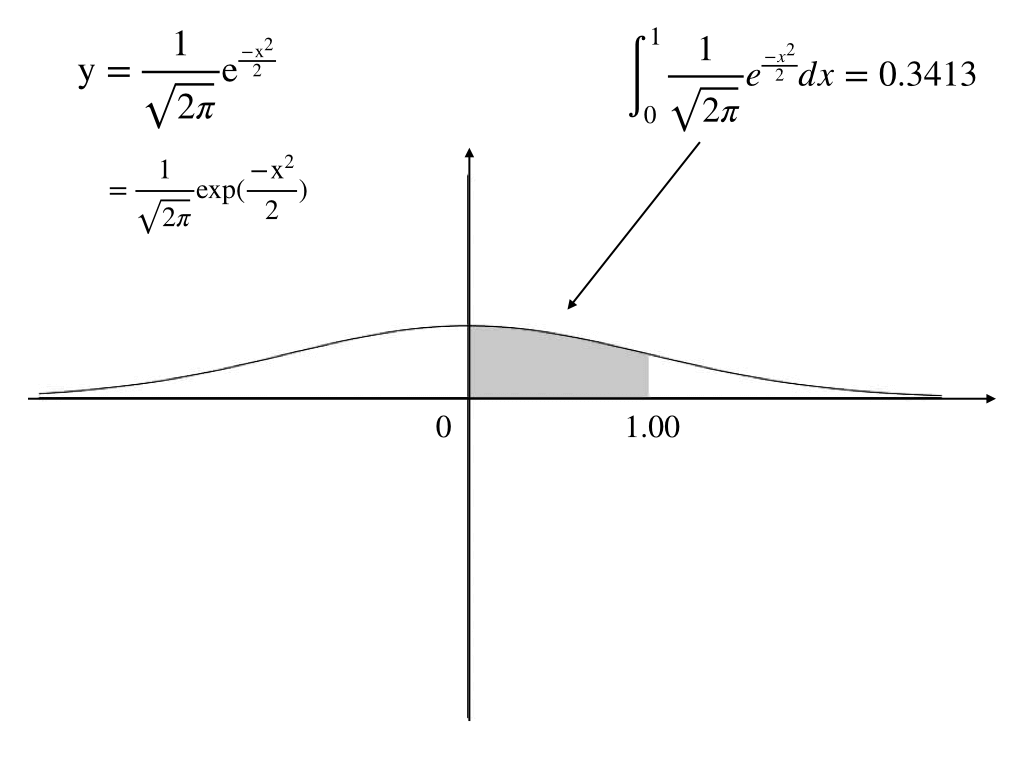
ここで塗りつぶした部分の面積、すなわち0から1の面積(=確率)は
$$\int_{0}^{1}\frac{1}{\sqrt{2\pi}}exp(\frac{-x^{2}}{2})\approx 0.3413$$
したがって、0.3413・・・(答)
(標準)正規分布表の読み取り方
実際に、検定やテストなどではf(x)を積分することによって区間の確率を求めることは現実的ではありません。(計算が大変すぎます。。)
そこで、以下のような正規分布表が与えられます。
これを読み取ることで、実際に積分を行わずとも必要な確率を求めることができます。
※:以下の分布表(*)は、”0”から”z”までの確率を表したものを用いています。
これ以外にも、\(z から\infty\)までを表した分布表(**)もあり(こちらの方が一般的)、その場合は0.00の値が0.5000(=総面積1で、確率密度関数が偶関数であることから、半分である\(0\rightarrow +\infty は0.5\)になります。)になります。
\(z から+\infty\)の表(**)を(*)から作るには、(*)のすべての値を0.5000から引けばOKです。
(どちらの表なのか一度使う前にチェックしておきましょう。)
step1:確率を求めたい区間の範囲を調べる
先ほどの例では、区間の”始まりが0”〜”終わりが+1”という分かりやすい範囲でしたが、
・-0.5~0.5のように0をまたいでマイナスからプラスまでの場合や、
・2〜3のように区間の始まりor終わりが0ではない場合
には、それぞれ少し工夫が必要なのでまず区間をチェックします。
step2:片側の確率を求める
範囲がマイナスから始まっているときは、正規分布のグラフの対称性を利用します。(参考:「偶関数と奇関数とは?」)
つまり、-0.5~0の値は0~0.5までの値と同じです。
次に、区間が0から始まっていないor(これも対称性から)0で終わっていない場合を考えます。
このような場合は、(2.0~3.0を例にすると)まず0〜3の値を求め、そこから0〜2までの値を引くことで求めたい確率を得ることができます。
step3:小数第一位までを縦軸で探す
では実際に、0.00~1.00までの確率を求める方法を紹介します。
まず、整数(1の位)+小数第一位(ここでは1.0)が等しい行を縦軸で探します。
(下の分布表の上から11行目です)
step4:小数第2位を横軸で探す
次に、小数第2位(ここでは1.00の.00の部分です)の値と等しい列を横軸で探します。
(同一列目です)
step5:交点が求めたい確率
こうして正規分布表を見てみると、たてが1.0、よこが0,00が”交差”する地点は”0.3413”(黒枠で囲んでいます)となっており、
たしかに先ほど正規分布曲線を(0,1)の区間で定積分した値と一致します。
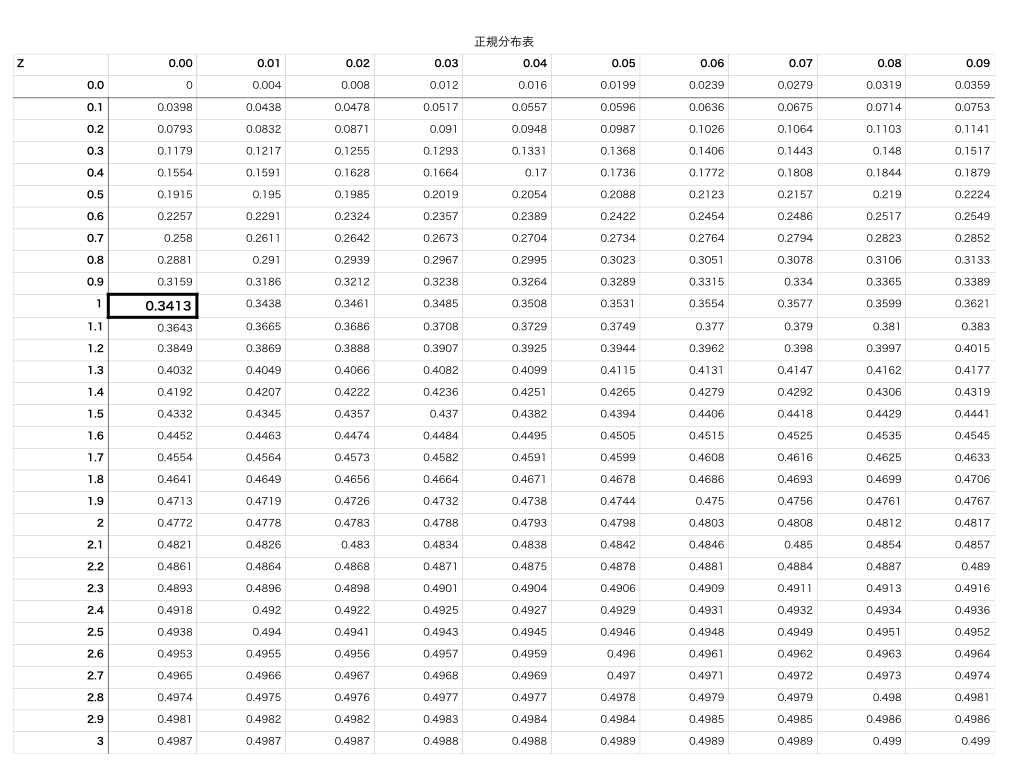
<正規分布表(*):スマホなどでご覧の方は拡大してください>
(エクセルや、macのNumbersでは、NORMSDIST関数と(ROUND関数←四捨五入して桁数を指定)を組み合わせることで、簡単に上のような表を作成できます。)
正規分布のまとめ
・正規分布と”標準化をする意味”
・標準正規分布の分布曲線(=確率密度関数)の式を覚えておきましょう
これから、何度も何度も繰り返し使用することになるので、
・正規分布表の『読み取り方』をしっかりマスターしておきましょう
次回:ポアソン分布へ〜
第五回:「ポアソン分布とその関連」
(NEW!!}:「統計学とデータの分析のまとめページ」
最後までご覧いただき有難うございました。
【総合学習メディア】:「スマナビング」では、読者の皆さまからのご感想を募集しています。
ぜひコメント欄にお寄せください (※:”個々の問題や証明の質問”には、対応出来ない場合があります。)

