連立方程式を行列で解く!その仕組みをわかりやすく解説

線形代数の原点「連立方程式」を行列を使って解いてみよう

今回は、これまでの線形代数シリーズ（参考：「線形代数を０から学ぶ解説記事まとめ」）で学んだことを使いながら、線形代数が生まれた原点である「連立方程式の解を求める」方法を紹介します。

行列と連立方程式(1)

ここまでの線形代数シリーズでは、逆行列・行列式・行列の演算などを紹介してきました。

今回は、それらを使って基礎的な連立方程式を解く方法を解説します。

ここでは二元一次連立方程式を扱いますが、これは次回以降の３元１次（３×３）の基本となる部分なので、しっかりと流れを習得しておきましょう。

（続編完成しました：「３×３行列とサラスの公式・掃き出し法による３元一次方程式の解き方」）

連立方程式を行列の積で表そう

まず問題の連立方程式を以下に示します。

5x+3y=4・・・(1)

2x+y=1・・・(2)

当然この程度であれば消去法ですぐに解けますが、わざわざ行列を使って解く理由は、方程式・未知数の数が大きくなった際に、サイズの大きな行列を利用して解を求める”理屈”を知るためです。

では、この２元一次方程式を行列の形で表してみます。

「行列どうしのかけ算をわかりやすく！」の回で紹介したように、(1),(2)は行列の積の形で表すことができます。

$$\underbrace{\begin{pmatrix}
5 & 3 \\
2 & 1
\end{pmatrix}}_{Aとする}\begin{bmatrix}
x \\
y
\end{bmatrix}=\begin{bmatrix}
4 \\
1
\end{bmatrix}\cdots ※$$

$$\underbrace{\begin{pmatrix}
5 & 3 \\
2 & 1
\end{pmatrix}\begin{bmatrix}
x \\
y
\end{bmatrix}}$$

この部分の積を計算すると、確かに元々の連立方程式に戻ります。

では、・・・※の(x,y)を求めるにはどうすればよいでしょうか。

逆行列と行列式

ここで登場するのが、逆行列です。（参考：「逆行列とは？行列の割り算と行列式の意味」）

逆行列と”もとの行列”の積は単位行列Eとなり、実数で言うところの”逆数をかけて1にする”ことと同じような役割を果たしました。

また、行列式を調べることでその行列が逆行列を持つか調べることができました。

そこで、行列Aの行列式を計算すると（上のリンクを参考にしてください）、$$\det A=5・1-2・3=-1≠0 $$より、行列式が０でないので逆行列が存在します。

ここからは、$$\det A=|A|$$ と表記します。

$$A^{-1}=\frac {1}{|A|}\begin{pmatrix}
1 & -3 \\
-2 & 5
\end{pmatrix}$$

$$=\left( -1\right) \begin{pmatrix}
1 & -3 \\
-2 & 5
\end{pmatrix}より、$$

$$逆行列：A^{-1}=\begin{pmatrix}
-1 & 3 \\
2 & -5
\end{pmatrix}$$

ここで、※の式の両辺に逆行列A^-1をかけることで、

$$（左辺）＝\underbrace{\begin{pmatrix}
-1 & 3 \\
2 & -5
\end{pmatrix}\begin{pmatrix}
5 & 3 \\
2 & 1
\end{pmatrix}}_{単位行列Eとなる}\begin{bmatrix}
x \\
y
\end{bmatrix}$$

$$(右辺)=\begin{pmatrix}
-1 & 3 \\
2 & -5
\end{pmatrix}\begin{bmatrix}
4 \\
1
\end{bmatrix}$$

次に、（右辺）は単位行列Eの性質より（参考：「線形代数１：線形代数の基礎と様々な行列」）

$$(右辺)=\begin{bmatrix}
x \\
y
\end{bmatrix}$$

のみとなるので、あとは（左辺）を行列のかけ算の手順に従って計算すれば、

（x、y）を求めることができます。

従って、

$$\begin{bmatrix}
x \\
y
\end{bmatrix}=\begin{pmatrix}
-4+3 \\
8-5
\end{pmatrix}$$

ゆえに、（x.y）＝（-1,3）//

逆行列が存在しないとき

ここまでの例では、|A|≠0で逆行列が存在してくれたため、うまく解をつけることができましたが、行列式：|A|=0の際にはどうなるのでしょうか？イラストを使いながら詳しく紹介します。

不定解と不能

今回解いた２元一次方程式は、座標上の直線で表すと以下の図のようになり、その交点がである（-1,3）が解でした。

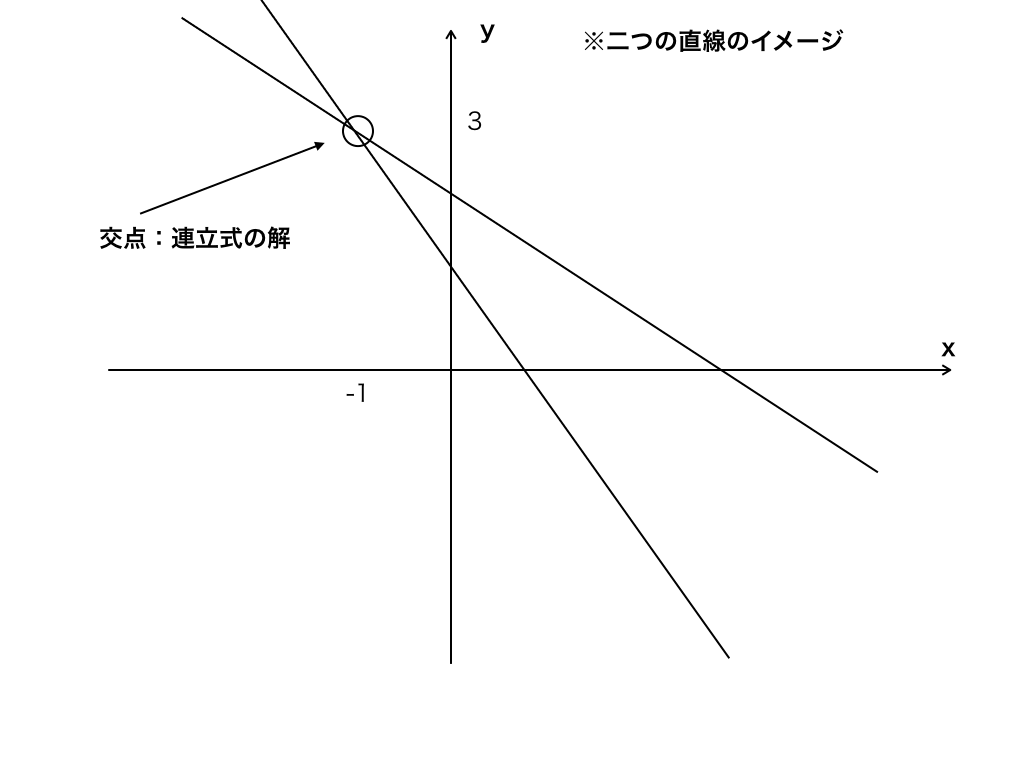
＜連立方程式の解と座標上の２直線の交点＞

一方で、逆行列が存在しない、すなわち行列式|A|=0の時は以下の２パターン存在します。

・直線どうしが平行でどこまでも交わらない場合

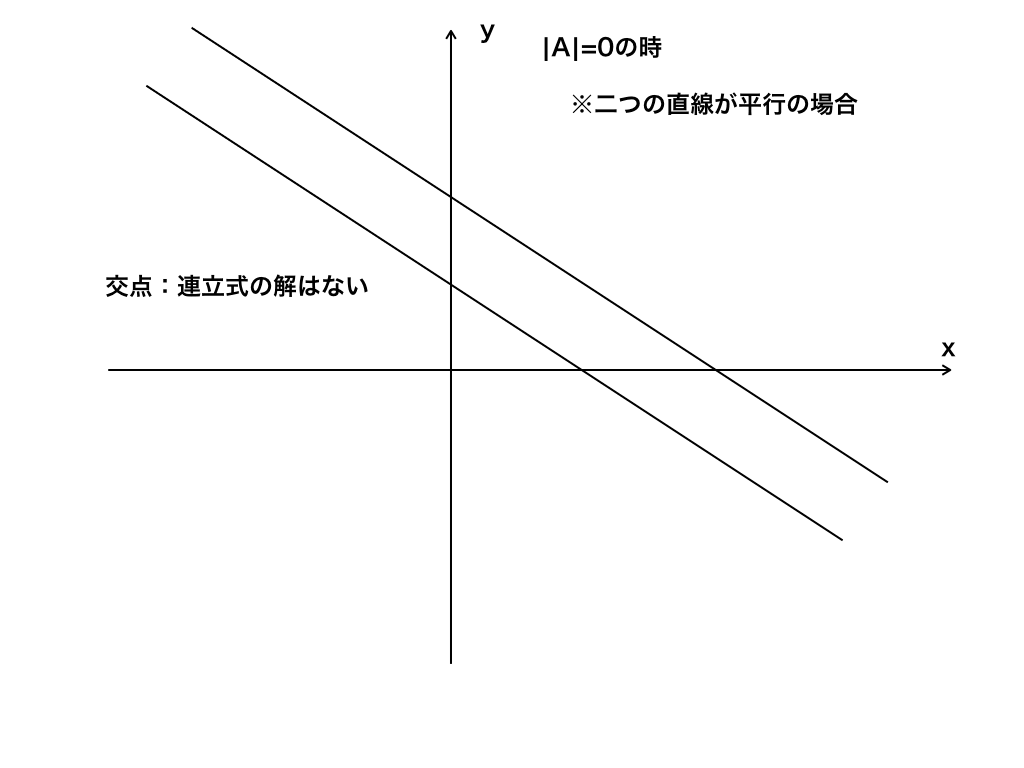
このように、永遠に交わらない＝解を持たないことを『不能』といいます。

・直線が一致して、すべての値が解になるため（x、y）の組みが定まらない

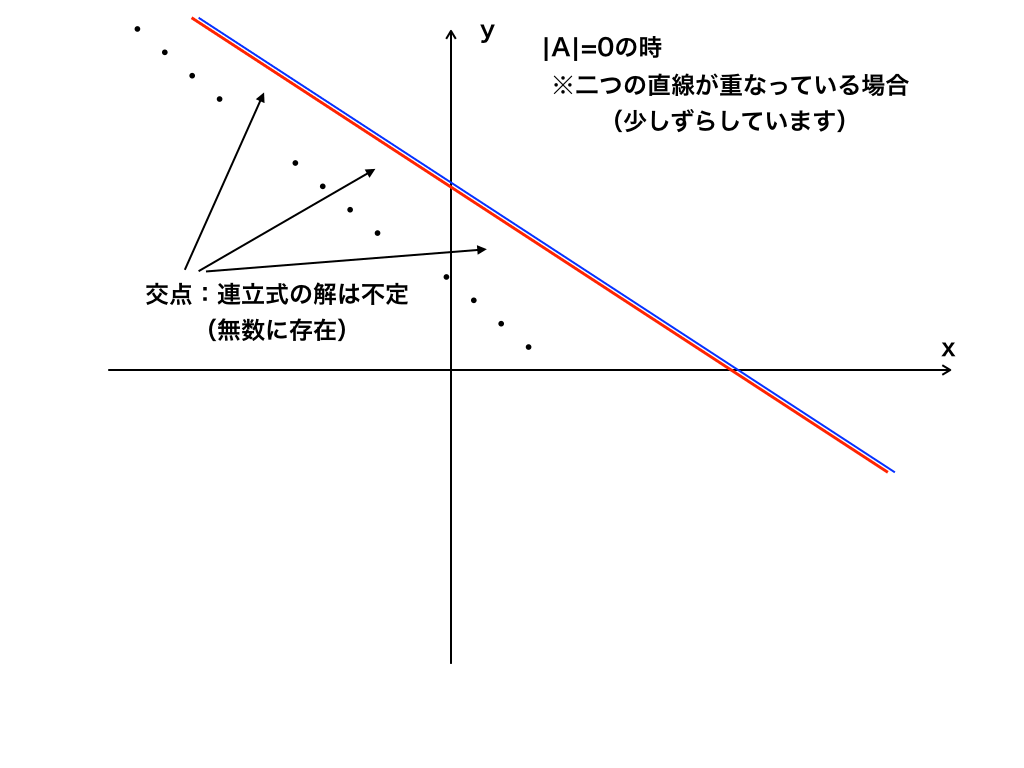
こちらは、解が定まらないの名の通り『不定解』といいます。

（整数の不定方程式も解が無数にあるため『整数であると言う条件』を使うことで解を絞り込みました。：「不定方程式のユークリッドの互除法を利用した会の求め方」）

不定と不能の見分け方

これらの見分け方は、『係数と定数項の比』の注目することです。

例として

a₁x+b₁y=c

と

a₂x+b₂y=d

の連立方程式を考えてみます。

a₁:a₂=b₁:b₂ であれば、二つの直線の傾きは等しくなるため、「重なる (不定解)or平行(不能解)」のどちらかであることが分かります。

さらに、定数項のcとdの比に注目して

a₁:a₂=b₁:b₂=c:d の時、２直線は完全に一致→不定解を持つ

（3x+y=1と6x+2y=2 を例にして考えると、3:6=1:2=1:2 で、この二つの直線は一致します）

a₁:a₂=b₁:b₂≠c:dの時、２直線は傾きが同じで切片が異なる→永遠に交わらないので解なし「不能」

と判別できます。（同様に、3x+y=5と6x+2y=3 の場合、傾きは一致するものの、y切片が5/3と1/2で平行を保ち交点を持ちません）

この比の関係と直線の交点の図を関連づけて頭に入れておきましょう。

まとめと3×3行列での掃き出し法へ

今回は、『２×２の行列を使った２元１次連立方程式の解を求める』と言う単純なものでした。

しかし、先述したように、今後紹介していく３×３行列、・・・と未知数や式の数がどんどんと大きくなっていった際でも通用する、基本的かつ重要な考え方を含んでいます。

成分の数を増やすことで（サイズの大きな行列）膨大なデータを扱うことができるので、機械（コンピューター）と相性が良く、現代においてはなくてはならないものです。

線形代数（行列）の応用分野の中でも、特に近年注目されているものが、AI（とその一部である機械学習・深層学習）です。

この分野に興味があれば、ぜひ→「機械学習のための数学と関連記事まとめ」、「機械学習シリーズ第1回：回帰分析」のシリーズを読んでみてください！

線形代数をはじめから!シリーズ一覧

線形代数のこれまでの記事は、＞＞「線形代数の解説記事まとめ」＜＜をご覧ください。

続編完成しました。

＞＞「線形代数(8)３×３行列とサラスの公式・掃き出し法による３元一次方程式の解き方」＜＜

最後までご覧いただきありがとうございました。

『スマナビング！』では、読者の皆さんのご意見や、記事リクエストの募集を行なっています。ぜひコメント欄にお寄せください。

また、B！やシェア、公式Twitterのフォローをしていただけると励みになります。

・お問い合わせやその他のご依頼に付きましては、お問い合わせページからご連絡下さい。