区分求積法を0から理解
<この記事の内容>:「区分求積法の式が記号だらけでよくわからない・・・」といった人を対象に、
・数列や極限の内容を復習しながら、
・わかりやすいイラストで区分求積法を理解して、
・最終的に標準的な問題が解けるレベル(※:区分求積法の問題を解くpointとコツ・解法の流れ)まで解説しています。
・2019年12月29日:”区分求積法によって極限を求める”応用問題(logを取る階乗型・範囲が異なるタイプ)とその解き方を追加しました!
<関連記事>:「極限を0から分かりやすく!解説まとめ」、「数3の微分・積分法とその応用まとめ」
目次(タップした所へ飛びます)
区分求積法とは(公式と準備編)
冒頭でも述べましたが、区分求積法は式を見ただけで難しく感じてしまう人が多いです。
区分求積法の公式と”日本語訳”
まだ始めは式の説明が理解出来なくても構いません。
(後半の解説編に入ってから”日本語訳”を見ると理解できるようになっています。)
$$\lim _{n\rightarrow \infty }\sum ^{n}_{k=1}\frac {1}{n}f\left( \frac {k}{n}\right) =\int ^{1}_{0}f\left( x\right)dx$$
(日本語に訳してみます):この式は、範囲が”0から1まで”の関数のf(x)とx軸で囲む面積が、n分割された長方形の面積\(f(x)\times \frac{1}{n}\)の総和の極限と等しいことを示しています。
・・・
まだ『よく分からない』ですね。気にせずに、次に進みましょう。
(確認)シグマ記号や極限の復習
この公式の理解には、\(\sum\)と\(\lim_{n \rightarrow \infty }\)の知識が必須です。
総和の記号については「Σの意味と数列の和の公式を徹底解説」、極限の中でも”和”を扱った「無限級数と無限等比級数」で復習しておきましょう。
区分求積法の公式の解説(理解と応用編)
さて、ここまでの準備(復習)編で区分求積法の理解に必要な知識は揃いました。
ここから本題の式をマスターし、最後の確認問題で”どのように使用するか”まで解説していきます。
面積の分割と総和の極限
いきなり、区分求積法の式(n→∞)の場合を見ても『?』だったので、一旦nを具体的で小さな数ならばどうなるか、を試します。
※(『分からない』→『実験する』は、どんな分野でも役立ちます。参考:「整数問題の解法が思い付かないとき」)
さて、小さな値として式中の:n=2の場合を考えてみましょう。
すなわち、$$\sum ^{2}_{k=1}\frac {1}{2}f\left( \frac {k}{2}\right)$$の時、この式は以下の図の”2つの長方形の面積を足した値”を表しています。
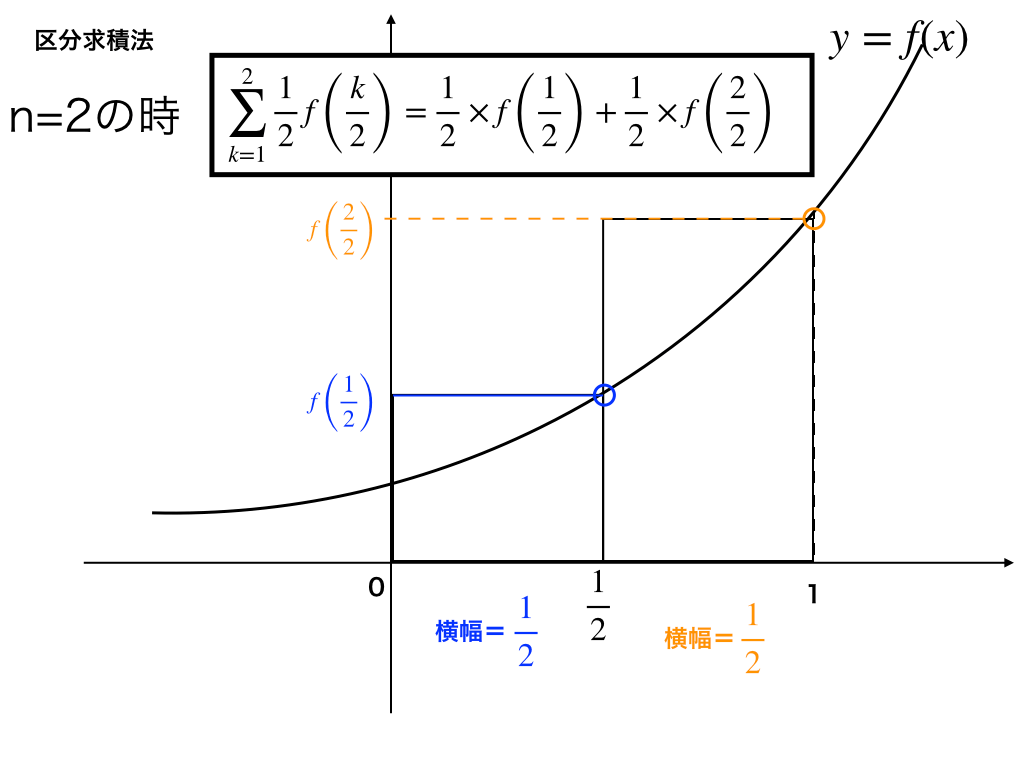
まず\(\frac{1}{n}のnが2\)、なので
(n=1の時の長方形)『横幅が0から1/2の1/2、高さはf(1/2)』(図中で青色で塗りつぶしている部分です)。
もう一つの(n=2)の時の長方形は、『横幅1/2で、高さf(2/2)=f(1)』(オレンジ色で塗りつぶしている部分)
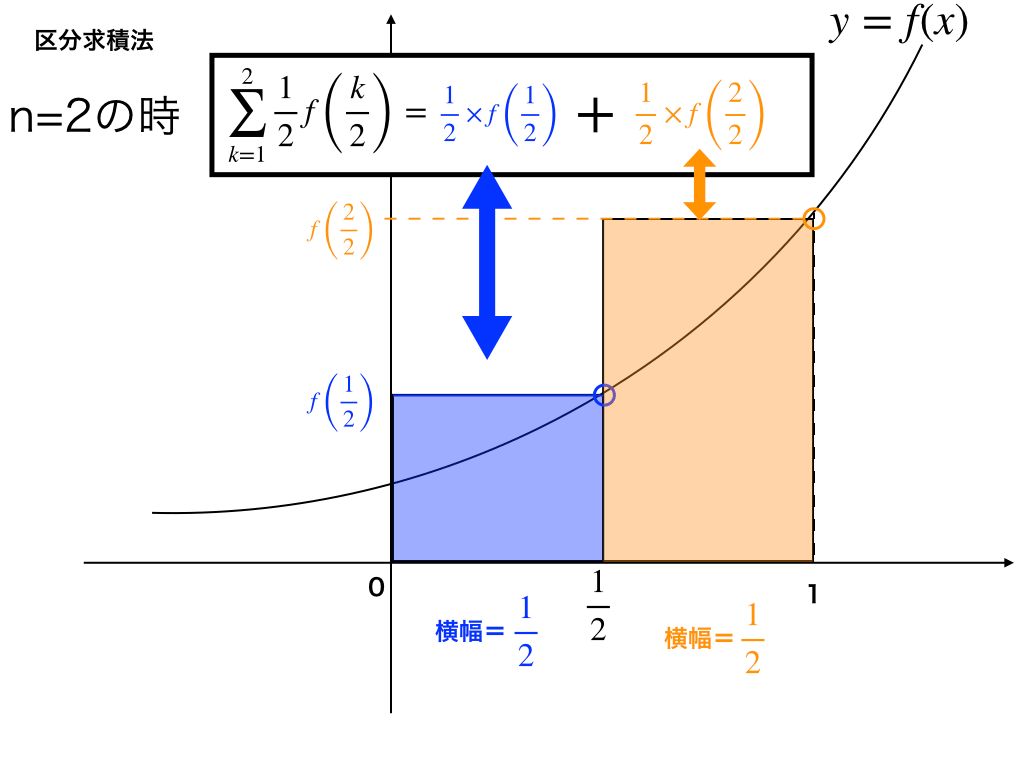
この2つの面積を足し合わせることで、積分区間が0から1のf(x)とx軸を囲む面積(始めに『日本語訳』したところ)に近づきました。
ただしこれだけではまだ問題があります。
余分な面積を減らすには・・・
以下の斜線部をみてください。
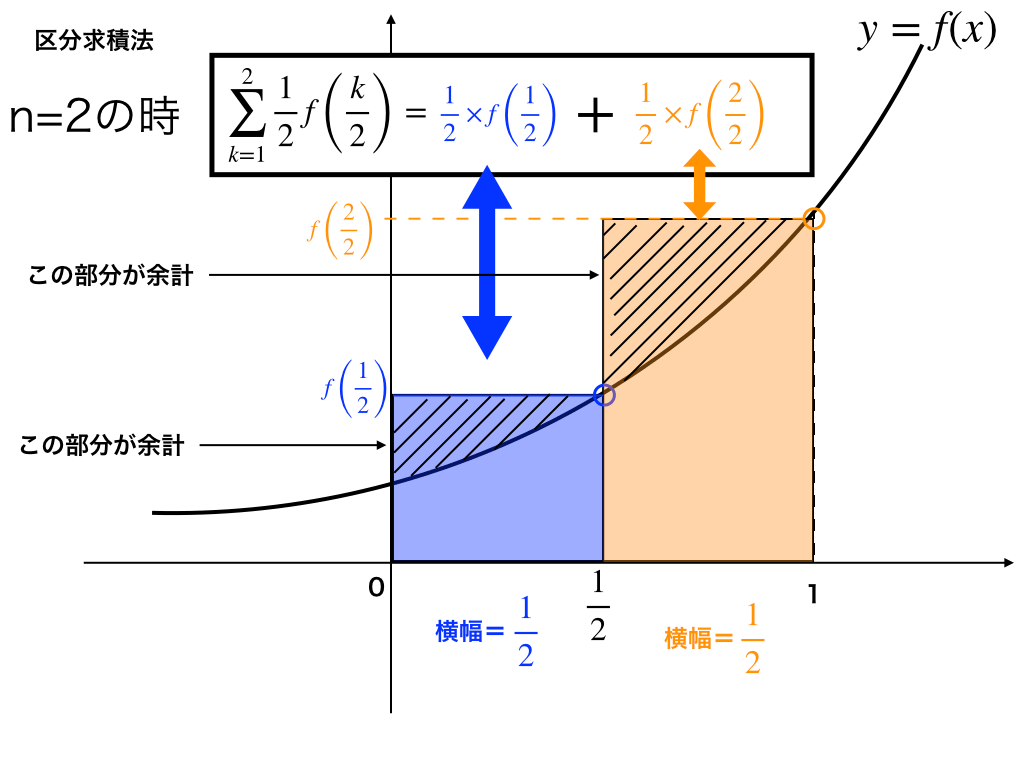
先ほどの図の長方形の面積のうち、余計な部分に斜線を引いたものです。
この斜線部が無くなれば\(=\int^{1}_{0}f(x) dx\)の値と一致するはずです。
ここで【\(\lim_{n\rightarrow\infty}\)】が役に立ちます。
nを無限大に近付けていくと”横幅”である”1/n”が限りなく”0”に近付き、同時に”余計な面積”も0に向かいます。
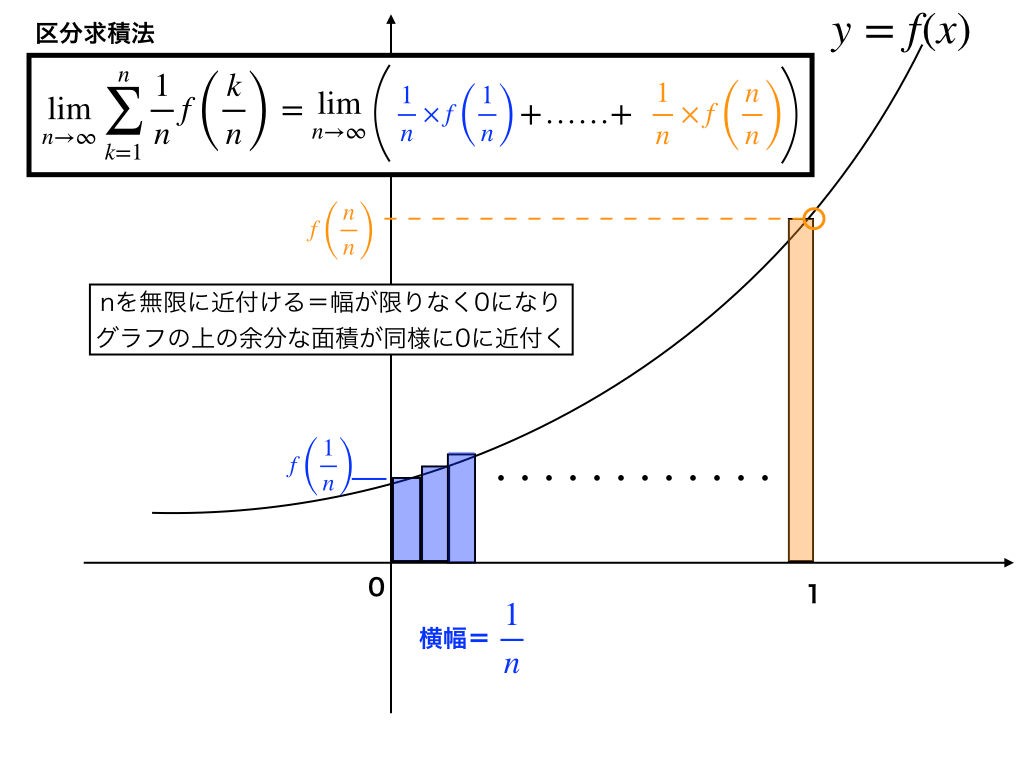
そして\(\lim_{n\rightarrow\infty}\)によって、0〜1までの面積と=で結ぶことが可能になります。
これが、$$\lim _{n\rightarrow \infty }\sum ^{n}_{k=1}\frac {1}{n}f\left( \frac {k}{n}\right) =\int ^{1}_{0}f\left( x\right)dx$$区分求積法の公式の意味です。
確認例題(使い方)
実際に、この式をどのように使っていくのか確認問題を見ながら紹介していきます。
問:次の極限の値を求めよ。
$$\lim_{n\rightarrow\infty}\frac{1}{n}(\frac{n^{2}}{9n^{2}+1}+\frac{n^{2}}{9n^{2}+4}+\ldots +\frac{n^{2}}{9n^{2}+n^{2}})$$
解答解説:(k/n)を作る事がPOINT!
見出しにもあるように、式の中から\(\frac{k}{n}\)のカタチをみつけて(作り出して)、区分求積法の公式→積分計算、という順番を踏むことが最大のポイントです。
今、問題の式の()内の分母は\(n^{2}-◯^{2}\)になっています。
さらに、分子は\(n^{2}\)であることから、分母分子をnの2乗で割ってあげることで、$$\frac{1}{9-\frac{1}{n^{2}}}+\frac{1}{9-\frac{2^{2}}{n^{2}}}+\ldots$$となって、$$\sum^{n}_{k=1}\frac{1}{9-(\frac{k}{n})^{2}}$$で表すことができます。
つまり、$$\lim _{n\rightarrow \infty }\frac {1}{n}\sum ^{n}_{k=1}\frac{1}{9-(\frac{k}{n})^{2}}$$
区分求積法の式より、
(k/n)=x なので、\((k/n)^{2}\)=\(x^{2}\)
したがって、$$=\int ^{1}_{0}\frac{1}{9-x^{2}}dx$$
の定積分の値が問の答えとなります。
部分分数に分解することで、(参考:「部分分数分解の仕方とコツ」)
$$=\frac{1}{6}\int ^{1}_{0}(\frac{1}{3-x}+\frac{1}{3+x})dx$$
$$=\frac{1}{6}\left[ \log \frac {3+x}{3-x}\right] ^{1}_{0}=\frac{1}{6}\log{2}$$
よって、\(\frac{1}{6}\log{2}\ldots (答)\)
区分求積法の応用問題
ここからは、よく入試などで問われる区分求積法の例題を掲載していきます。
区分求積法とlog(対数を取る場合)
一つ目は”log”を取るタイプです。対数の重要な性質(【真数の肩に乗っている部分を前に持ってくる】ことが出来る+【真数の掛け算は対数の足し算】として表すことが可能、etc,,,)
によって、一見するとかなり複雑な問題を比較的簡単にすることができます。
(参考;「対数について詳しく解説」)
階乗やP・Cとlogの融合version
区分求積法を使う問題で、logが大事な役割を担うのは、「n!」などの階乗やP・C(順列・組合せ)などの記号が入った問題を扱う場合です。(参考2:「場合の数と確率で扱う記号(ページ前半部分)」)
<例>\(n!=1・2・3・\cdots (n-1)・n\)
より、対数をとると\(\log{n!}=\log{1}+\log{2}+\cdots+\log{n}\)
とできるので、$$=\sum_{k=1}^{n}\log{k}$$とすることが出来ます。
(※:logを取ってから区分求積法で求めた値を『そのまま答えにしないように』注意が必要です。あくまでも計算できる・楽になるように勝手にlogを取っているので、最後にはlogを外してあげる必要があります。)
問題(難問?):logの扱い方と注意点
$$\lim _{n\rightarrow \infty }\sqrt[n] {\frac {{}_{4n} C_n\cdot \left( n!\right) }{{}_{2n} P_n}}$$
この式の極限以外の部分に注目して、順列Pの公式と組合せCの公式もすべて階乗の形になおしてあげると、
$$\left( \frac {(4n) !\cdot (n!) ( n!) }{\left( 3n\right) !\cdot (n!) \cdot \left( 2n\right) !}\right) ^{\frac {1}{n}}$$
これを整理すると、
$$\left(\frac{4n(4n-1)\cdots(3n+1)}{2n(2n-1)\cdots(n+1)}\right)^{\frac{1}{n}}$$
この部分のlogを取って区分求積の形に持ち込みます。
$$=\lim _{n\rightarrow \infty }\frac{1}{n}\sum ^{n}_{k=1}\log{\frac{3n+k}{n+k}}$$
$$=\int_{0}^{1}\log{\frac{3+x}{1+x}}dx$$
\(\int \log{x}dx=x\log{x}-x+Const.\)より、(logxの不定積分)
\(=[(3+x)\log(3+x)-(3+x)-\)
下に続きます。
\((1+x)\log(1+x)+(1+x)]_{0}^{1}\)
\(=\log{256}-\log{4}-\log{27}=\log{(\frac{64}{27})}\)
最後にlogを外して、答え:\(\frac{64}{27}\)
積分区間(範囲が1→nでない)タイプ
これは最も簡単な応用かもしれません。シグマの範囲が\(\sum_{k=1}^{2n}\)などのk=1〜nまででは無い場合です。
具体的には、足し合わせる範囲に応じて積分区間が変わります。
$$\lim _{n→ \infty }\sum ^{3n}_{k=1}\frac {3k^{2}+n^{2}}{n^{3}+n^{2}k+k^{3}}$$
\(\frac{1}{n}\)のくくりだし(コツ)
ここで、pointとして分母/分子のnの次数が同じになるように、前に\(\frac{1}{n}\)を持っていきます。
$$\lim _{n→ \infty }\frac{1}{n}\sum ^{3n}_{k=1}\frac {3nk^{2}+n^{3}}{n^{3}+n^{2}k+k^{3}}$$
分母分子を\(n^{3}\)で割って、$$\lim _{n→ \infty }\frac{1}{n}\sum ^{3n}_{k=1}\frac {3\frac{k^{2}}{n^{2}}+1}{1+\frac{k}{n}+\frac{k^{3}}{n^{3}}}$$
よって、区分求積法より
$$\int_{0}^{3}\frac{3x^{2}+1}{1+x+x^{3}}dx=[\log{(x^{3}+x+1)}]_{0}^{3}=\log{31}$$
上の定積分は、分母の微分が分子にあるタイプです。
区分求積法まとめと関連記事へ
さて、初見ではシグマ:\(\sum\)やインテグラル:\(\int\)、極限\(\lim_{n\rightarrow \infty}\)が入り乱れて、難しそうな「区分求積法」の式でした。
しかし、n=2のような場合を使って簡単な(小さな)場合から考えていくと理解出来たのではないでしょうか。
この記事で基本となる意味と使い方は身に付いているので、残りは問題集等でどんどん演習を進めて下さい!
極限・微積分の応用記事
今回も最後までご覧いただき、有難うございました。
「スマナビング!」では、読者の皆さんのご意見や、記事のリクエストの募集を随時コメント欄にて行なっています。
また、お役に立ちましたら、シェアやTwitterのフォローをしていただけると励みになります。
・お問い合わせ/ご依頼その他に付きましては、お問い合わせページからご連絡下さい。