ニュートン法と近似値計算
<この記事の内容>:数学3の微分法で頻出の『ニュートン法』の仕組みと意味を、イラストと例題を用いて紹介しています。
また、プログラミングでニュートン法に触れる大人の方にも最適です。
<関連する記事>:「数学三の微分法・積分法の記事まとめ」/「機械学習に必要なキソ数学知識まとめ」(参考:「最急降下法(勾配降下法)の仕組みとは?」)
目次(タップした所へ飛びます)
ニュートン法の意味と仕組み
まずは、”『ニュートン法』とは一体なんなのか?”について解説します。
ニュートン法とは?
ニュートン法というのは、ある関数f(x)とy=0の交点(つまり0=f(x)の解ですね)を求めるための方法といえ、このニュートン法をうまく利用してあげる事で無理数などの近似値を計算することができます。
とはいえ、文字よりも以下のイラスト(と、後ろに掲載している問題)を見た方が理解しやすいはずなので、早速進めていきましょう。
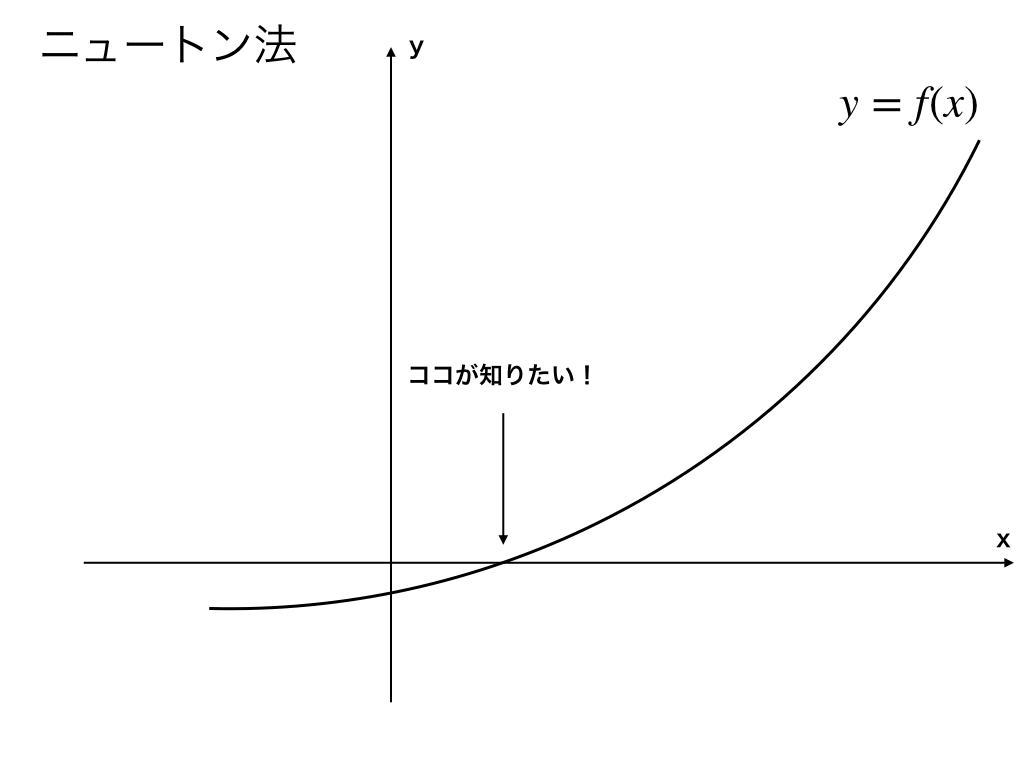
<図中の\(f(x)=0\)を求めたい>
図解”近似値”が求まる仕組み
先述した通り、近似値が求まるしくみは”百聞は一見にしかず”です。
手順1つずつにイラストを付けて紹介します。
まず先ほど紹介した図から始めます。
其の1:適当な値をとって(x,f(x))を求める
最初に、\(f(x)=0\)の解よりも大きい”適当な”値\(x_{1}\)をとります。
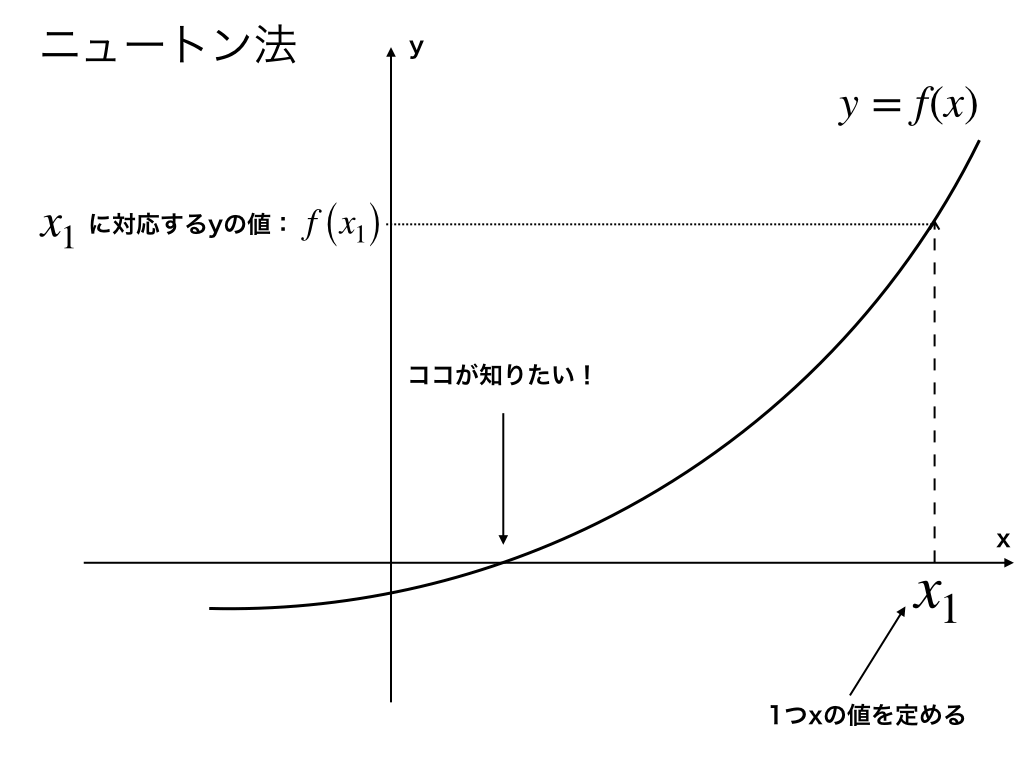
すると、f(x)のグラフ上で\(x_{1}\)に対応した\(f(x_{1})\)が求まります。
其の2:接線を引く
次に、(其の1)での\(x_{1},f(x_{1})\)を接点とする接線(以下の青色の直線)を引きます。
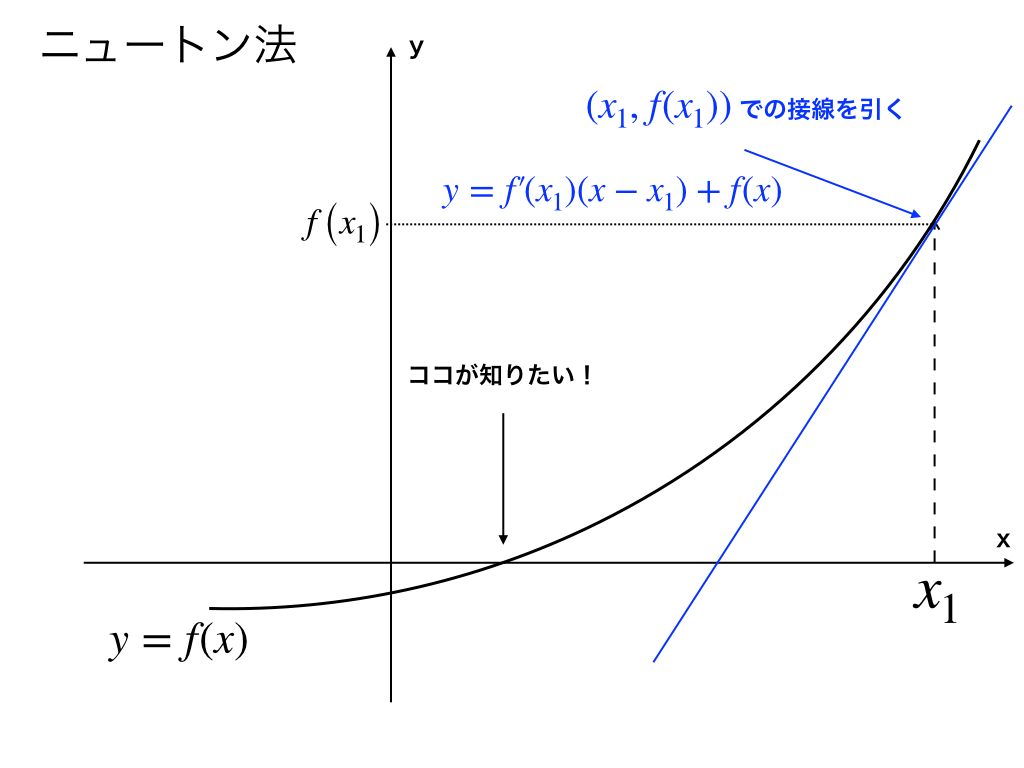
ここでの接線は、次の式で表すことが可能です。\(y=f'(x_{1})(x-x_{1})+f(x_{1})\)
(参考記事:【微分法】接線の方程式と法線の方程式の求め方)
其の3:接線とy=0との交点を求め→新たに接線を引く
次に注目するのは、青色の接線とx軸(y=0)との交点です。
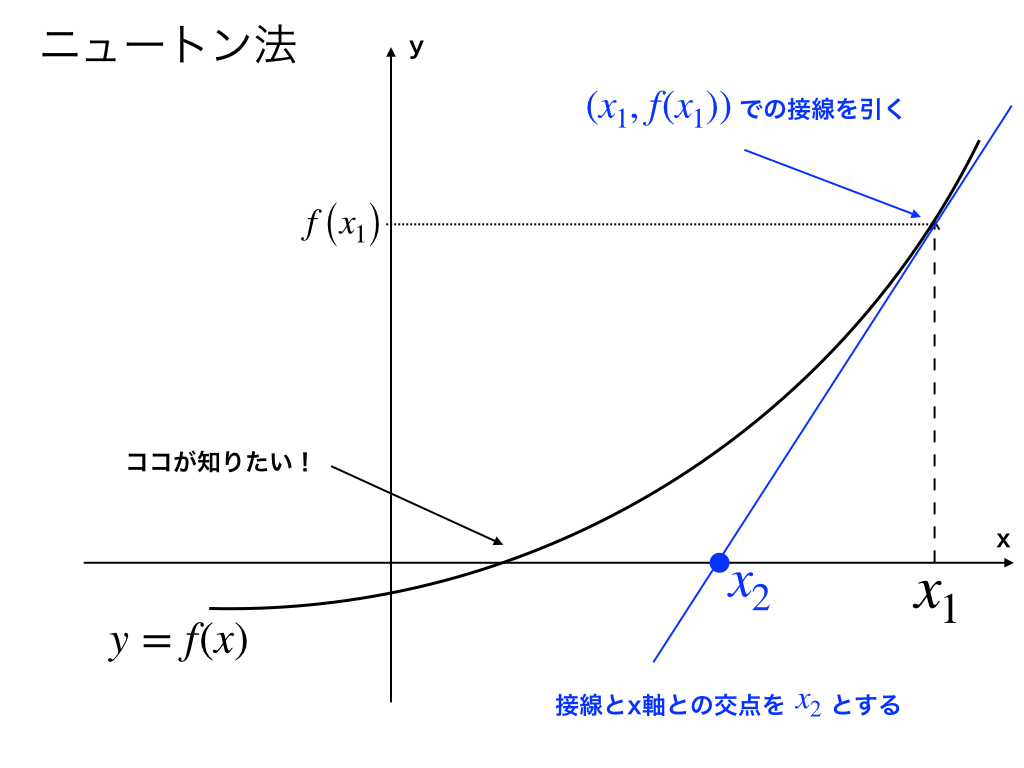
上の図のように、交点(接線の式=0の解)を\(x_{2}\)とし、先ほどと同様に\((x_{2},f(x_{2})\)を接点とする接線(次の図の赤色の部分)の方程式を求めます。
其の4:操作を繰り返す
これをどんどんと繰り返して行くことで、急速に求めたい値に近付いていきます。
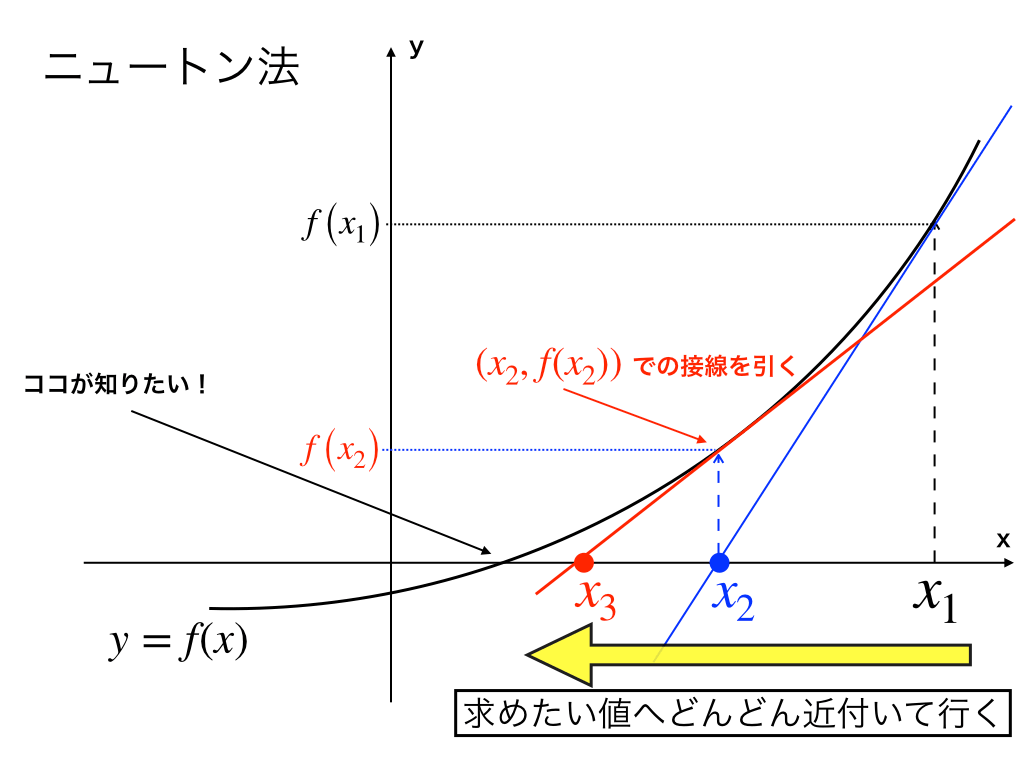
これが、大雑把ですが”ニュートン法で近似値が求まる仕組み”です。
ニュートン法の証明問題を解いて理解
この項では、具体例を用いて(高校数学の範囲で)ニュートン法を証明していきます。
ルート5の近似値を求める
5の平方根(\(\sqrt{5}\))は、語呂合わせで2.23692,,,と覚えている人も多いかと思います。
ここでは、\(f(x)=x^{2}-5\)を使って求め方と証明をしていきます。
ちなみに、実際の入試では次のように出題されます。
漸化式を作る
ニュートン法を用いて近似値の計算を行うときは、ここで作った漸化式に具体的な数値を代入して計算を繰り返します。
ただし、入試では近似値を求める計算問題よりも(2)、(3)の証明問題がより重要です。
まず、\(y=f'(x_{n})(x-x_{n})+f(x_{n})\)が接点(n,f(n))での接線の式でした。
\(x_{n+1}はこの式とy=0との交点\)だったので、展開して整理すると、\(x\cdot f'(x_{n})=x_{n}\cdot f'(x_{n})-f(x_{n})\)。
ここで両辺を\(f‘(x)で割り、x=x_{n+1}=\)のカタチを作ります。
(先ほどの図の様に、\(x_{1}\)での接線のy=0との求めた\(交点xはx_{2}\)と置いていました。\(x_{n}の場合\)も同様です。)
したがって、問われている\(x_{n+1}とx_{n}の関係=漸化式\)は、$$x_{n+1}=x_{n}-\frac{f(x_{n})}{f'(x_{n})}$$
さらに、$$f(x_{n})=x^{2}_{n}-5なので、f'(x_{n})=2x_{n}$$より、
答えとなる漸化式は、$$x_{n+1}=x_{n}-\frac{x^{2}_{n}-5}{2x_{n}}$$
と表すことができます。
数学的帰納法の利用
ここから(2)を解くには、数学的帰納法の知識が必要なので、必要な方は「数学的帰納法の仕組みと使い方」←を参照してください。
さて、(2)では\(x_{n}>\sqrt{5},n=1,2,\ldots\)を証明する問題でした。
見出しに書いてしまっていますが、『自然数+全ての〜+証明』が揃った場合は大抵が帰納法を利用する事になります。
早速回答を作っていきましょう。
まず(一):n=1の時、問題文より\(x_{1}>\sqrt{5}\)
次に、(二):n=kの時、\(x_{k}>\sqrt{5}\)が成り立つと仮定する。
(メモ:n=k+1のときにも\(x_{k+1}>\sqrt{5}\)が成り立つことを示せば良いので、$$ x_{k+1}-\sqrt{5}>0$$である事を示す様に式変形をしていきます。)
\(x_{k+1}=\frac{1}{2} (x_{k}+\frac{5}{x_{k}} \)より、$$ x_{k+1}-\sqrt{5}=\frac{x^{2}_{k}-2\sqrt{5}x_{k}+5}{2x_{k}}$$
ここで、分子が\((x-\sqrt{5})\)の二乗の形=(0以上)に変形でき、分母部分は(二)の仮定を用いて、\(x_{k}>\sqrt{5}>0\)より$$x_{k+1}>\sqrt{5}$$。
よって、数学的帰納法より全ての自然数nに対して\(x_{n}>5\)が示せた。
解けない漸化式の極限
さて、(2)はこれから行う(3)の誘導です。
(『解けない漸化式の極限』については別記事を作成予定です)
目的は\(\lim_{n\rightarrow\infty}x_{n}が\sqrt{5}\)に収束するということを証明すれば良いので、
$$x_{n+1}-\sqrt{5}=\frac{(x_{n}-\sqrt{5})^{2}}{2x_{n}}= \frac{x_{n}-\sqrt{5}}{2x_{n}}(x_{n}-\sqrt{5})$$
ここで、\(\frac{x_{n}-\sqrt{5}}{2x_{n}}\)の部分・・・(※)は、\(=\frac{1}{2}-\frac{\sqrt{5}}{2x_{n}}\)で\(x_{n}\)は常に\(\sqrt{5}\)より大きかった(2で示しました)ので、\(\frac{\sqrt{5}}{2x_{n}}<\frac{1}{2}\)。
したがって(※)は0<(※)<1/2 と言えます。
収束の証明(はさみうち!)
最後に、はさみうちの原理を用います(参考:「極限での”はさみうちの原理”を分かりやすく!」)
よって、$$(x_{n+1}-\sqrt{5})<\frac{1}{2}(x_{n}-\sqrt{5})$$
この右辺をn=1になるまで繰り返していくと・・・
$$\frac{1}{2}(x_{n}-\sqrt{5})<\ldots <(\frac{1}{2})^{n}(x_{1}-\sqrt{5})$$
よって、\(\sqrt{5}<x_{n}\)と合わせて、
$$0<(x_{n}-\sqrt{5})<(\frac{1}{2})^{n}(x_{1}-\sqrt{5})$$
はさみうちの原理より、$$\lim_{n\rightarrow\infty}(\frac{1}{2})^{n}(x_{1}-\sqrt{5})=0$$
したがって、$$\lim_{n\rightarrow\infty}x_{n}=\sqrt{5} ・・・(答)$$
ニュートン法まとめ
ここまで見てきたように、ニュートン法を題材にした問題はかなりややこしく、それ故に特に難関大でよく出題されます。
ぜひ、何度か復習しておいてください。
関係する記事へ(極限・漸化式・機械学習etc,,,)
極限については「極限を得意にするための記事6選+α」
数列と漸化式については「漸化式の解き方12タイプを完全網羅」
機械学習関係は「機械学習に必要な高校・学部1年レベルの数学」
最後までご覧いただきまして、有難うございました。
当サイト、 「スマナビング!」では、読者の皆さんのご意見・ご感想・記事のリクエストの募集を行なっています。 ぜひコメント欄までお寄せください。
また、お役に立ちましたらsnsでB!やシェアをしていただけると励みになります。
・お問い合わせ/ご依頼に付きましては、お問い合わせページからご連絡下さい。

