次数下げで計算速度を大幅にアップする方法【計算テクニック】

次数下げをうまく使って計算を高速化

＜計算速度と数学力＞：計算速度は入試において非常に重要な要素です。

時間的な余裕が生まれる”だけ”でなく、計算を工夫して『時短』することを考えながら日々の問題を解いていくことで、不思議と『数学力』がついてくるのです。（数学３では、これがさらに顕著になります）

この記事では、そんな計算速度を上げる工夫（テクニック）を集めています。

具体的には、「x4+x3+x2=?(x=1+i)」のような、式の値を求める問題で次数が高く、条件式に虚数単位"i"やルート√などが入っている場合の対処法を解説します。

次数下げで計算を早くする:厄介な数を移行して二乗せよ！

『次数下げ』と呼ばれる方法を解説していきます。以下に出てくる問題例はいずれも”複素数a+biの虚数単位"i"”や、ルート（平方根）など少し厄介な数を含んでいる場合です。

この様な問題では、真面目に代入して計算してはいけません。（計算速度が落ちるだけでなく、計算ミスを起こしやすくなります）

まず、(1)ルート・(2)複素数の入った式での次数下げの基本（これだけでも計算スピードがアップします）を始めに学びます。

最後(3)で、『多項式の割り算』と『基本となる次数下げ』を融合させて最もスマートに解く方法を解説します。

ルートの入った条件式での次数下げ(1)

問題例：\(x+\sqrt{2}+1=0\)の時、\(x^{4}+2x^{3}+x…(一)\)の値を求めよ

これをまともに条件式を変形して、x＝-√2-1を４乗・３乗と計算して代入するわけにはいきません。

合言葉は「厄介な文字を分離して２乗」です。ここではルート２が当てはまります。

ルートを右辺へ移項(分離)

したがって、\(x+1=-\sqrt{2}と\sqrt{2}\)を移項し、2乗してみると・・・

\(x^{2}+2x+1=2 \)これでルートが消えました。

さらに続けてx²=の形にするために2x+1を右辺へ持っていきます。

こうすることで、\(x^{2}=-2x+1,x^{2}:2次をx:1次\)に下げることができる様になりました。

しかし、問題はx⁴+2x³+xの値を求める事だったので、x³とx⁴が必要です。

そこで、

x²にxを掛ける

という操作を行います。つまり、\(x^{2}=-2x+1\)の両辺にxを掛けることで、\(x^{3}=-2x^{2}+x\),

更に"x²=-2x+1"は先に求めているので、xの二乗の部分に代入してあげると

\(x^{3}=-2(-2x+1)+x→∴x^{3}=5x-2\)

これでxの３乗もxの一次式で表せました。

最後に、xの４乗を求めるのですが、これも同様に今導いた『x³＝（５x−２）』の両辺にxを掛けて右辺にできたxの２乗を代入すると簡単に計算できます。

\(x^{4}=5x^{2}-2x⇔x^{4}=5(-2x+1)-2x\)

\(∴x^{4}=-12x+5\)

xの(n乗=xの１次式)を全て代入

これで問題の式（1）のxの４乗、３乗をxで表すことができるようになったので、あとは各々代入すると

(一)は\(-12x+5+2(5x-2)+x=-x+1\)

更に\(x=-\sqrt{2}-1\)だったので\((一)=\sqrt{2}+2\)

これが徐々にxの次数を下げていく””次数下げ "のテクニックの第一歩です。

虚数単位i(複素数)が入った条件式での次数下げ(2)

もう一題、今度は複素数バージョンを解いてみましょう。（ルートの次数下げを理解できた方は先に自分で回答を作ってみてください。

問題例：x+3i+1=0の時

\(x^{3}+3x^{2}+x+1…(二)\)の値を求めよ

解説:虚数を分離せよ！

ルート同様、ここでの厄介な数は【虚数3i】です。したがって、x+1=-3iとして2乗し、\(x^{2}+2x+1=-9\)、ただし\((i^{2}=-1に注意！)\)となります。

\(x^{2}=-2x-10\)

（二）ではxの３乗まで必要なので、問題(1)同様両辺にxを掛け、新たにできたxの二乗のところに代入すると、\(x^{3}=-2x^{2}-10x、x^{3}=-2(-2x-10)-10x\)

\(∴x^{3}=-6x+20\)

\((二)=-6x+20+(-6x-30)+x+1=-11x-9\)のxにx=-1-3iを代入すると、

(二)=2+33i

次数下げと式の割り算を使う【本題】

ここまでの上２つ例題を通して、次数下げの仕組みが理解できたかと思います。

実際に４乗、３乗・・・として計算するのに比べると多少楽になりました。

はじめに書いた様に、いよいよこの項が「本題」です。

多項式の割り算と上述した次数下げを融合させることで、大幅に作業がショートカットできます。

（参考関連記事：「因数分解の仕方総まとめ」の”因数定理・剰余の定理”のところ）

問題３を通してその方法を紹介します。

問題３：$$x=2+\sqrt{3}の時,$$

\(2x^{4}+2x^{3}+x^{2}+x…(※)\)の値を求めよ

step1:ルートを分離して二乗！

これはいつも通りなのですが、（１）の場合と一つだけ違うのは、【『xの二乗＝△x＋○』という形にせず、『xの２乗＋△x＋○=0』の形に移項する点です】。

\(x-2=\sqrt{3}\)の両辺を2乗し、整理すると\(x^{2}-4x+1=0…(※※)\)

step2:求めたい式をstep1の式で割る

次に、\(2x^{4}+2x^{3}+x^{2}+x…(※)\)

を\(x^{2}-4x+1=0…(※※)\)で割ります。

式の割り算は以下の図の様に行います。ポイントは『係数だけ書く』ことです。

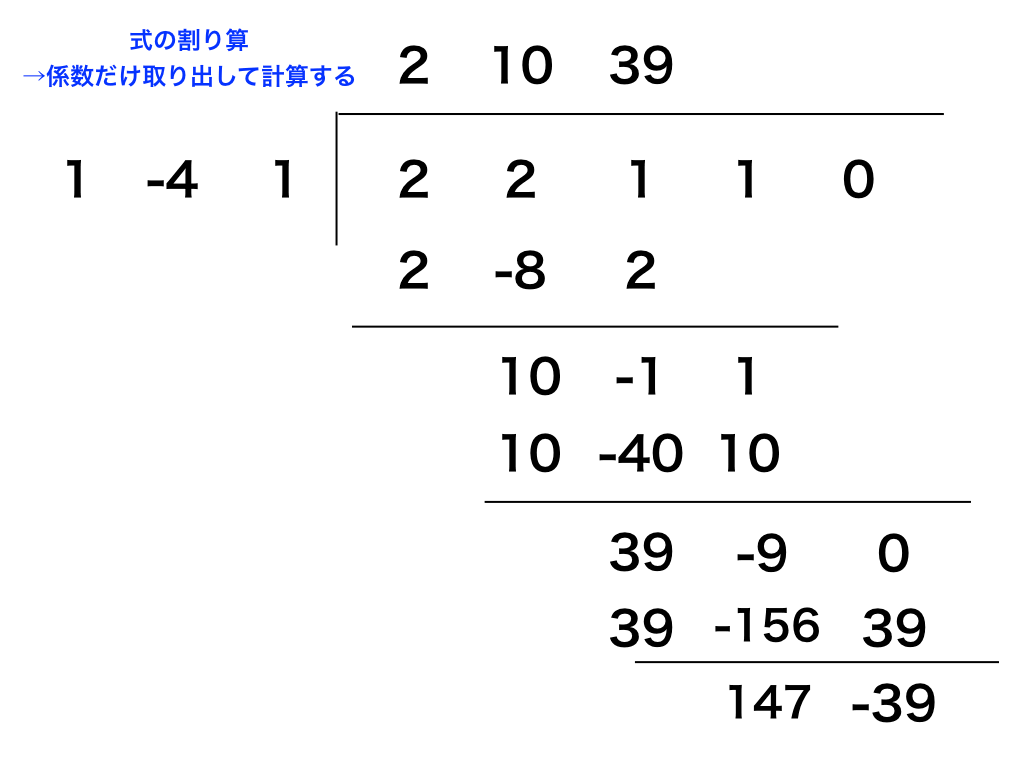
すると、\(商が2x^{2}＋10x+39\)、余りが147x-39となりました。

step3:※の式を割った式と商・余りの式で表す

これは、\(f(x)=2x^{4}+2x^{3}+x^{2}+x…(※)\)とすると、次の様に表すことができます。

\(f(x)=(x^{2}-4x+1)(2x^{2}＋10x+39)+147x-39\)

『元の割られた式＝割った式×商の式＋余りの式』のカタチです。

もしこれが分かりにくければ、普通の整数の割り算で考えると良いでしょう。

例：125を3で割ると41余り2となるので、125=(3)(41)+2 と書くことができますね？それと全く同じことです。

ここで、注目すべきは割った式です。

今x＝2+√3の時の（※）の式の値、言い換えるならばf（x)のxに2＋√３を代入した値が欲しいわけです。

\((x^{2}-4x+1)は(※※)より『０』でした!\)

step4:割る数=0を利用して余りに条件を代入して完成

ということは、f(x)=0(2x+10)+147x-39

f(x)=147x-39 なので、x=2+√3を代入すると、

\(147\sqrt{3}+255…（答え）\)

【本題】まとめ

こうすれば（１）、（２）の様に次数を一つ一つ下げることなく、

・厄介な数字を移行して２乗→＝0に整理

・式の割り算を行なって、結果を整理すると余りのみが残る

・余りの式にx＝を代入

と非常に効率的に計算することができます。

まとめと更なる応用記事

さて、例題３つを通して計算を高速かつミス無くする方法を紹介しました。

この様に、なるべく工夫して計算力を上げていく様にしましょう。＞＞「応用編：相反方程式と比例式の解き方」

数学のテクニック記事・関連記事まとめ

「数学Ⅲの微積分を得意にする方法：増減表を作るのは最終手段です！」

「弧度法に付いての二つの問題|π＝180°の理由とsin1、sin2、sin3の大小関係」

今回も最後までご覧いただき、有難うございました。

「スマナビング！」では、読者の皆さんのご意見、ご感想や、記事のリクエストの募集を行なっています。ぜひコメント欄までお寄せください。

お役に立ちましたら、B！やシェア、をしていただけると励みになります。

・その他のご依頼などに付きましては、お問い合わせページからご連絡下さい。