高次方程式と解と係数の関係【応用編】
<この記事の内容>:「二次・三次方程式での解と係数の関係」を利用して、「解の配置問題」(左の記事で解説)を楽に解く別解や、
『高次方程式での重解が関係する問題』の解法など、数学2の初めにぶつかる”苦手”な人が多い応用問題をまとめました。
目次(タップした所へ飛びます)
解の配置問題
ここでは、いわゆる『解の配置問題』を扱います。
数学1では後で紹介する方法:(判別式Dと、\(\frac{-2a}{b}:軸の位置\)、そしてy切片での値などを組み合わせる方法)で解いていました。
これを”解と係数”によって解く方法と『要注意point』を実際の例題を解きながら解説します。
解と係数の関係を利用する解法
次の2次方程式:\(x^{2}+(3k-1)x+(2k^{2}-1)=0\) の2つの異なる実数解が次の条件を満たすとき、kの範囲を求めよ。
(1):2つの解が共に正
(2):2つの解が共に負
(3):2つの解が共に3より小さい
(4):2つの解が共に1より大きい
解き方(答えと解説)
(1):さて、2つの異なる解が両方とも0以上なので、
\(x^{2}+(3k-1)x+(2k^{2}-1)=0\) の解を\(x=p.q\)とすると、
\(0<p、かつ、 0<q よって、0<p+q が言えます。\)
また、同様に\(p\cdot q>0 \)でもあります。
ここで、さっそく『二次の場合の解と係数の関係』を用いて、
\(p+q=-(3k-1) , p\cdot q=(2k^{2}-1)\)
故に、\(-(3k-1)>0:① 、かつ、 (2k^{2}-1)>0:②\)
さらに異なる2個の実数解を持つので、判別式をDとして、
\(D=(3k-1)^{2}-4(2k^{2}-1)>0:③\)も満たす必要があります。
数直線で整理する(1)
上で必要な三つの条件式を計算すると、
①は\(k<\frac{-1}{3}\)、
②は\(k<\frac{-\sqrt{2}}{2},or,k>\frac{\sqrt{2}}{2}\)、
最後にDの条件:③は\(k<1,or,5<k\)
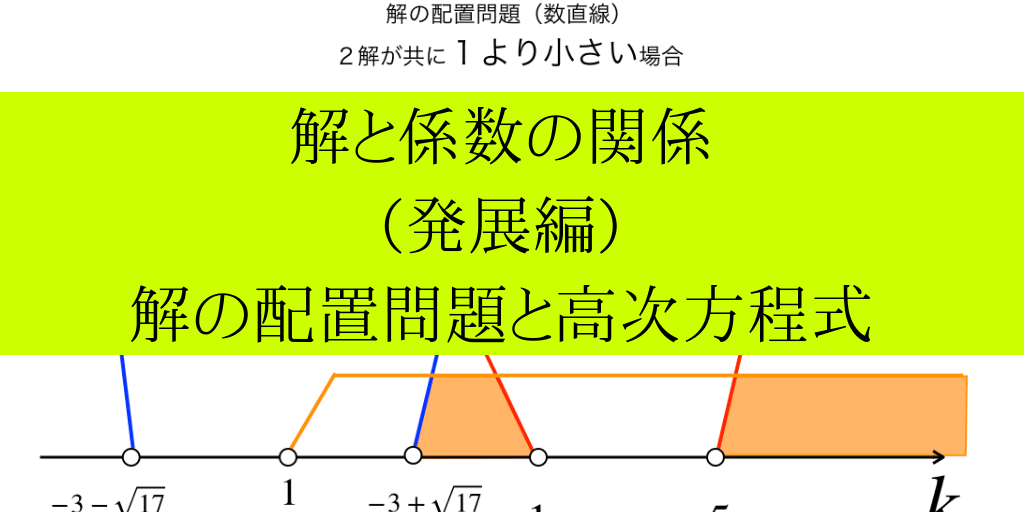
・これらの①〜③を数直線上に並べた時の【共通部分】が問題の答えである『kの範囲』となります。
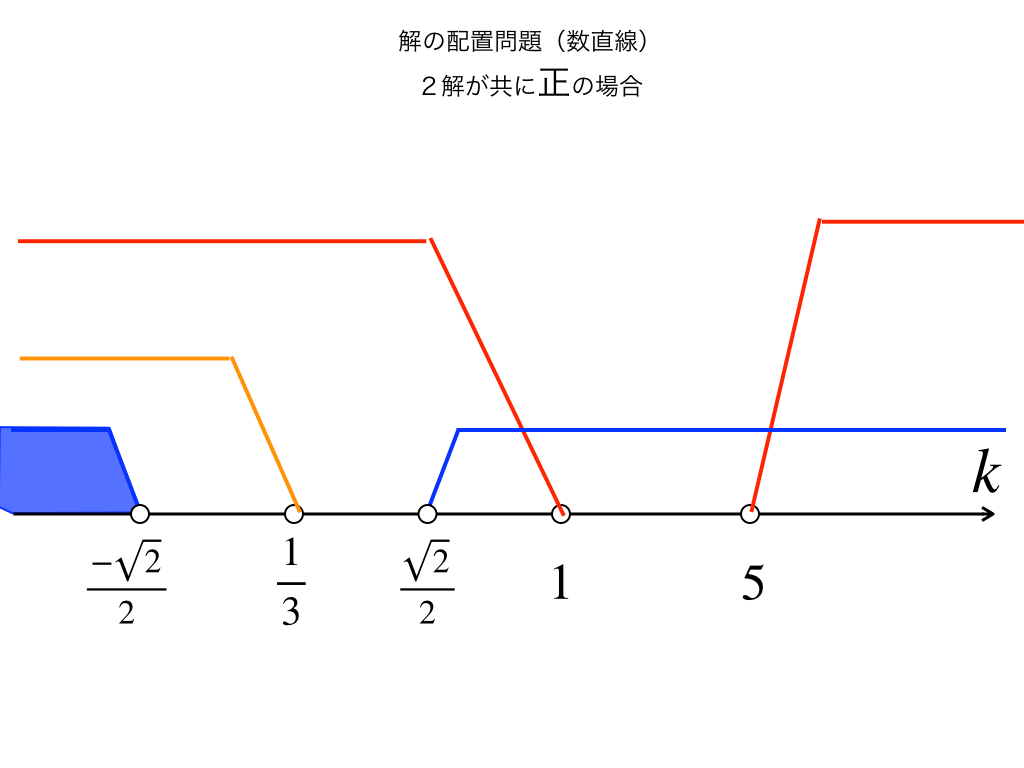
ゆえに、異なる2つの解が共に0より大きい場合のkの範囲は、\(k<\frac{-\sqrt{2}}{2}\)・・・(答)
・・・
(2):次は『異なる二つの解が共に0より小さい』場合なので、
\(0<p、かつ、 0<q よって、0<p+q が言えます。\)また、同様に\(p\cdot q>0 \)。
そして、判別式DについてはD>0はかわりありません。
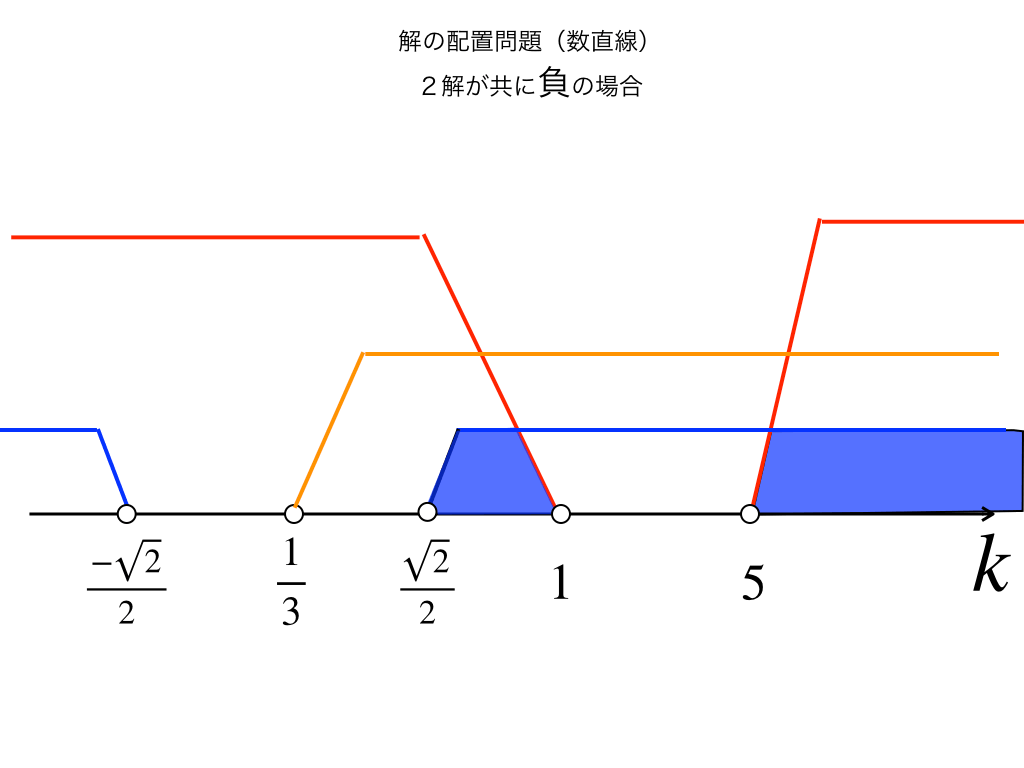
これらの条件を数直線で表すと上のようになります。(図2)
(2)について:計算を大幅にカットするコツ
(2)の数直線をかくにあたって、(1)と同様に計算しても良いですが、一部の条件の不等号(p+qとpqの条件)を逆にすれば、ほとんど計算せずに済みます。
(判別式:Dについては、不等号を逆転する必要すらなくそのまま使えます)
あとは、数直線上に並べて、(上の図2)$$\frac{\sqrt{2}}{2}<k<1,5<k$$・・・(答)
〜さて、1・2は比較的楽に理解出来たのではないでしょうか。この次の(3)・(4)は少し注意が必要です〜
問3・問4:2解が0以外の数を基準にする時(要注意!)
(3):『今度は0より大きい』や『0より小さい』といった場合ではなく、3より大きい場合を考えないといけません。
この場合も判別式Dの条件は変化しませんが、最重要な点が『p+q>3+3=6』、『p・q>9』と安易に設定してしまわないようにすることです。
例えば、p+q>6、かつ、p・q>9としてしまうと、次のような場合も含めてしまい題意を満たしません。
「p=2.9、q=4 」の場合、「p+q(和)は確かに6.9」と6より大きい条件を満たし、「pq(積)も=11.6」と9より大きいので2つの条件をクリアーしてしまいます。
しかし、pが2.9のため『2解がともに3より大きい』という大前提を満たせていません。
ではどのようにすればうまく条件を式で表せるのでしょうか?
・・・・・・・・・
この問題は次のように立式することで解決します。
$$(p-3)+(q-3)>0 、かつ、(p-3)\cdot (q-3)>0$$
式変形すると、$$p+q>6,かつ,(p-3)(q-3)>0$$これで、pやqが3以下の可能性を排除しつつ、問題の条件を満たす式を作ることができます。
よって、満たすべき式:$$判別式:D>0,p+q>6,かつ,(p-3)(q-3)>0$$
をそれぞれ計算して数直線上に表すと以下のようになります。
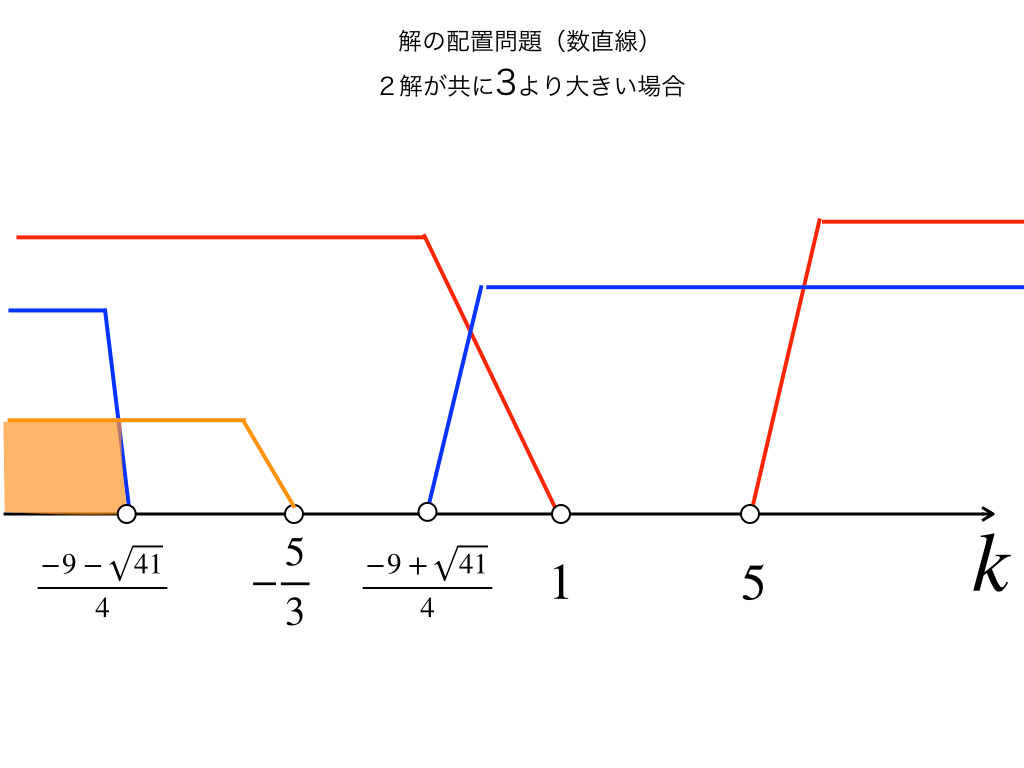
よって、$$\frac{-9-\sqrt{41}}{4}<k$$
(4):共に1より小さい値をとる場合でも、問三と同じ方法で解いていきます。
すなわち\((p-(-1)+(q-(-1))<0\)、かつ、\((p-(-1)\times (q-(-1))>0\)、\(最後に判別式D>0\)
これらを解いて連立し、数直線上に書き込みます。
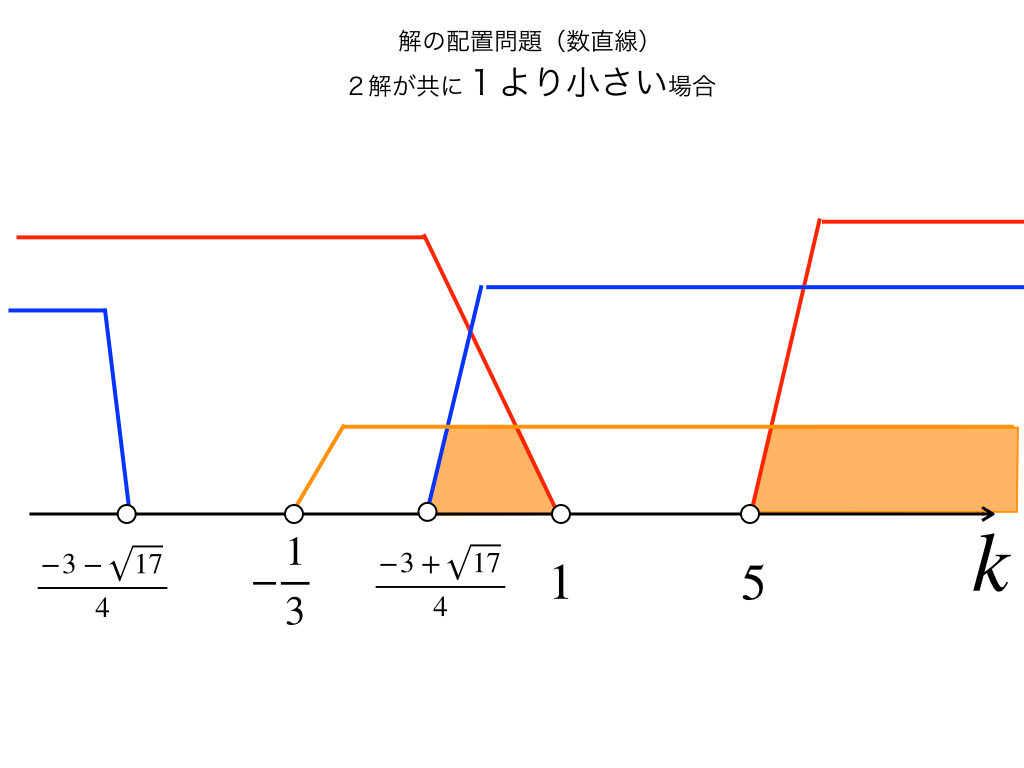
ゆえに数直線を見て、$$\frac{-3+\sqrt{17}}{4}<k<1、又は、5<k$$
軸・判別式・f(x)を用いる方法
参考:(1)を通常の方法:「軸・D・f(0)」を使って解いた場合も載せておきます。
$$f(x)=x^{2}+(3k-1)x+(2k^{2}-1) $$として、2つの異なる解が共に0より大きいので、次の三つの条件を満たす。
・判別式D>0・・・(一)
・軸>0・・・(二)
・f(0)>0・・・(三)
(一)より、\(D=(3k-1)^{2}-4(2k^{2}-1)>0\)
(二)より、軸は\(\frac{-(3k-1)}{2}>0\)
(三)より、\(f(0)=2k^{2}-1>0\)
それぞれ解くと、結果的に(1)での場合と同じになるため、 満たすべきkの条件は、\(k<\frac{-\sqrt{2}}{2}\)
満たすべきkの条件は、\(k<\frac{-\sqrt{2}}{2}\)
小まとめ
解の配置問題はこの2つの解法を両方身につけておくことと、
条件が正/負という0を基準にしないときにミスをしないように気をつけましょう。
高次方程式:2重解を持つ式
ここでは、高次(三次)方程式が二重解を持つ問題を通して、判別式や場合分けなどの仕方を学びます。
問題
いま、次のような3次方程式:\(x^{3}+(m-2)x^{2}+(2-2m)x-4=0\)がある。
この方程式が二重解を持つとき、定数”m”の値とその時の解を”全て”求めよ。
解答と解法の説明
まず初めに、因数定理を用います。
x=2を式に代入すると=0となることから、与式を(x-2)で割って因数分解を行います。
すると、下の図のように\((x-2)(x^{2}+mx+2)\)となって二重解の値によって場合分けすることになります。

まず(一):\((x^{2}+mx+2)\)が重解を持つ=重解の値≠2のとき。
このパターンでは、\((x^{2}+mx+2)\)の判別式が0であれば良いので、
\(D=m^{2}-8=0\)。これを計算すると、\(m=\pm 2\sqrt{2}\)
これを\((x^{2}+mx+2)\)に代入すると、xの値は\(x=\pm \sqrt{2}\)。
2つのxの解はいずれも≠2より、『m=\(\pm 2\sqrt{2}\)』のとき、xの解は「\(2,\sqrt{2}\),\(2,-\sqrt{2}\)」・・・(答1)
・・・・・・
次に(二):重解の値が“2”であり、\((x^{2}+mx+2)\)の解の片方が2、もう一方の値が≠2であるとき。
この場合、\((x^{2}+mx+2)\)の解の一つが2であることがあらかじめ分かっているので、与式に2を代入します。
\(4+2m+2=0\)より、m=-3、これより\(x^{2}-3x+2=0 \leftrightarrow (x-2)(x-1)=0\)。
ゆえに、xの2以外の解は1。
最後に(一)と(二):を合わせて、$$m=\pm 2\sqrt{2},-3 、その時の解はx=\pm \sqrt{2},1$$・・・(答)
今回のまとめ
解と係数の関係を使う問題は色々な分野で登場します。
また、解の配置問題に帰着するものとして、最難関大などで超頻出の「通過領域」などがあります。
今回の内容を身につけるとこう言った応用問題に対して非常に強力な武器になるので、以下の関連記事を合わせて読み、ぜひ自分のものにしてください!
関連する記事一覧
今回も最後までご覧頂きまして有難うございました。
このサイト「スマナビング!」では読者の皆さんのご意見、ご感想や、記事のリクエストの募集をコメント欄にて行なっています。
お役に立ちましたら、いいね!、B!やシェア、フォローをしていただけると大変励みになります。
・その他のお問い合わせ/ご依頼につきましては、お問い合わせページからご連絡下さい。

