圧平衡定数Kpの意味と求め方の解説と具体的な練習問題まとめ

”圧”平衡定数Kpとその関連問題の解説

＜この記事の内容：１＞：Kpで表される『圧平衡定数』の求め方を、理論化学の『気体』分野の解説をしながら紹介します。

＜記事の内容：２＞：Kpを求め、それを応用する練習問題に加えて、前回「化学平衡と（濃度）平衡定数Kc」で学んだ『濃度平衡定数：Kc』の具体的な問題を合わせて取り組みます。

”圧”平衡定数Kpとは?

”圧”平衡定数は、その名が示すように可逆反応を起こす反応において、分圧が平衡な状態になった時に求まる定数です。

Kpと”濃度”平衡定数Kcの違い

まず定数の文字の意味から見て見ましょう。

平衡定数はK（数学で学ぶ積分定数などでは、英語で定数を意味するConstantや、その頭文字”C”が用いられますが）、【化学で扱う定数】ではConstantのドイツ語訳：Konstanteの先頭の”K”を使います。

さらに、添え字としてpとcがついています。

pはPressure＝すなわち”圧力”なので、”圧”平衡定数を表したい場合にはKpを用います。

一方で、cは＝Concentration”濃度”、よって前回のような”濃度”平衡定数はKc、もしくはKで表します。

この他にも、溶解度積の分野で出現するKsp、加水分解定数Kh、etc,,,があるので注意しておきましょう。

圧平衡定数の求め方

以下のように、可逆反応である\(\alpha A+\beta B\leftrightarrow \gamma C+\delta D \)という反応が平衡状態となった場合には、

圧平衡定数は：$$K_{p}=\frac{p_{C}^{\gamma}p_{D}^{\delta}}{p_{A}^{\alpha}p_{B}^{\beta}}$$で求めることができます。

全圧・分圧と解離度

$$K_{p}=\frac{p_{C}^{\gamma}p_{D}^{\delta}}{p_{A}^{\alpha}p_{B}^{\beta}}$$

でそれぞれの\(p_{X}\)は、その気体の分圧を表し分圧の総和＝全圧が成り立ちます。（ドルトン分圧の法則）

また、反応物（左辺）が平衡状態でどの程度反応したか（生成物になったか）を『解離度』という値を使って求めることになります。（問題文で与えられます。）

KcとKpの練習問題編

では、具体的にKpを問題を使って求めていきましょう。

Kpを求める問題(四酸化二窒素と二酸化窒素)

練習問題１：いま、全圧\(2.0\times 10^{5}( Pa) \)を保った条件のもとで、「\(N_{2}O_{4}\)」から「\(2NO_{2}\)」が生成される可逆反応が起き、平衡状態となった。

この反応の解離度を"0.7"として、初めには\(NO_{2}\)が存在しなかったとき、各々の平衡状態での分圧と圧平衡定数Kpを求め、単位と併せて答えよ。

解答解説

圧平衡定数の問題では、大抵出題される物質が決まっていて、この四酸化二窒素の他には

・一酸化炭素

・ヨウ素、が頻出です。

さて、解説１に移ると初めは\(N_{2}O_{4}\)しか存在していないので、４酸化２窒素の分圧＝全圧となり、解離度が0.7（問題文より）であるので、

いつもの様に、反応の前→中→平衡時の表を作ってKpを求めていきます。

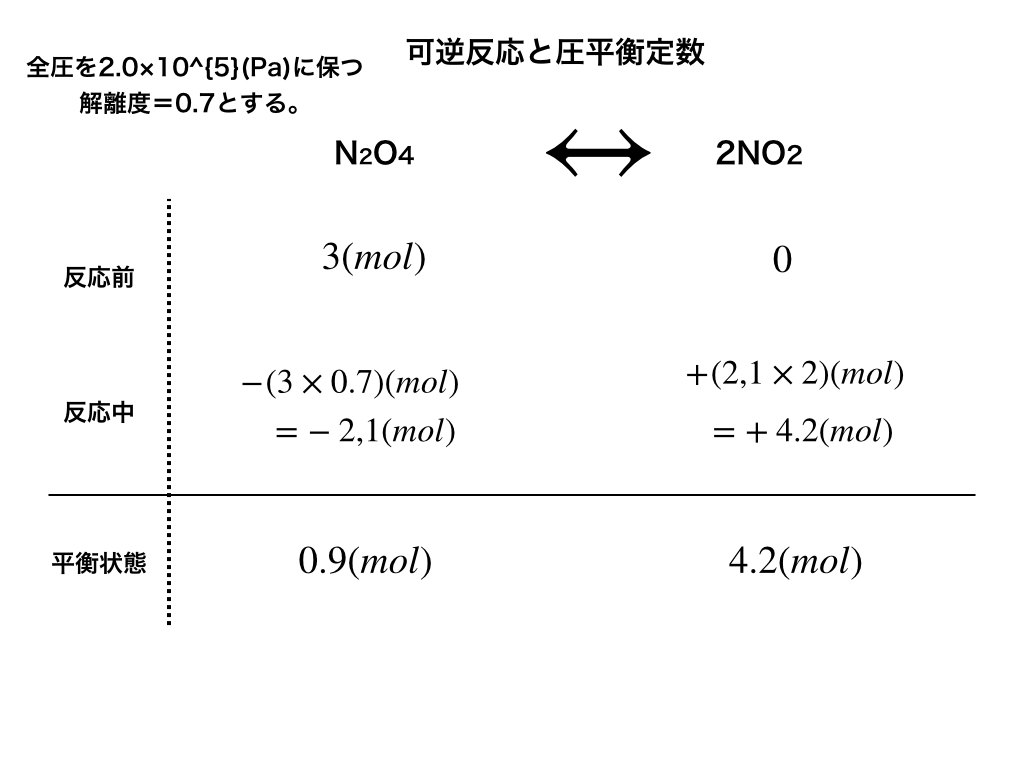
この様に、\(N_{2}O_{4}は0.9(mol),NO_{2}=4.2(mol)\)で平衡になった事がわかります。

ここで、全圧：\(2.0\times 10^{5}\)より四酸化二窒素の分圧は$$2.0\times 10^{5}\times\frac{0.9}{0.9+4.2}=\frac{6}{17}\times10^{5}(Pa)$$、二酸化窒素の分圧は$$2.0\times 10^{5}\times\frac{4.2}{0.9+4.2}=\frac{28}{17}\times 10^{5}(Pa)$$と求まるので、・・・（答え１）

上の紹介したKpの式にそれぞれの分圧を代入して、$$Kp=\frac{(\frac{28}{17}\times 10^{5})^{2}}{\frac{6}{17}\times10^{5}}$$

少し答えの値がきたなくなってしまいますが、計算を進めると\(Kp≒7.68\times 10^{5} (Pa)\)

\(∴Kp=7.7\times 10^{5}(Pa)\)・・・（答え２）

Kcの求値問題（ヨウ化水素の可逆反応）

前回は、Kcについて全て文字で与えて計算していましたが、今回は具体的な数値を用いて問題を解いていきます。

題材は、ヨウ素と水素からヨウ化水素が生成される可逆反応です。

練習問題２：いま、1(L)の容器中でヨウ素I：2(mol)と水素H_{2}：3(mol)からヨウ化水素：HIが生成される可逆反応が起き、平衡状態となった際には3(mol)のHIができた。

この時の（濃度）平衡定数Kcの値を単位付きで求め、解答せよ。

解答解説

解説２：普段通り反応の前→中→平衡の表を作ってKcを求めていきます。

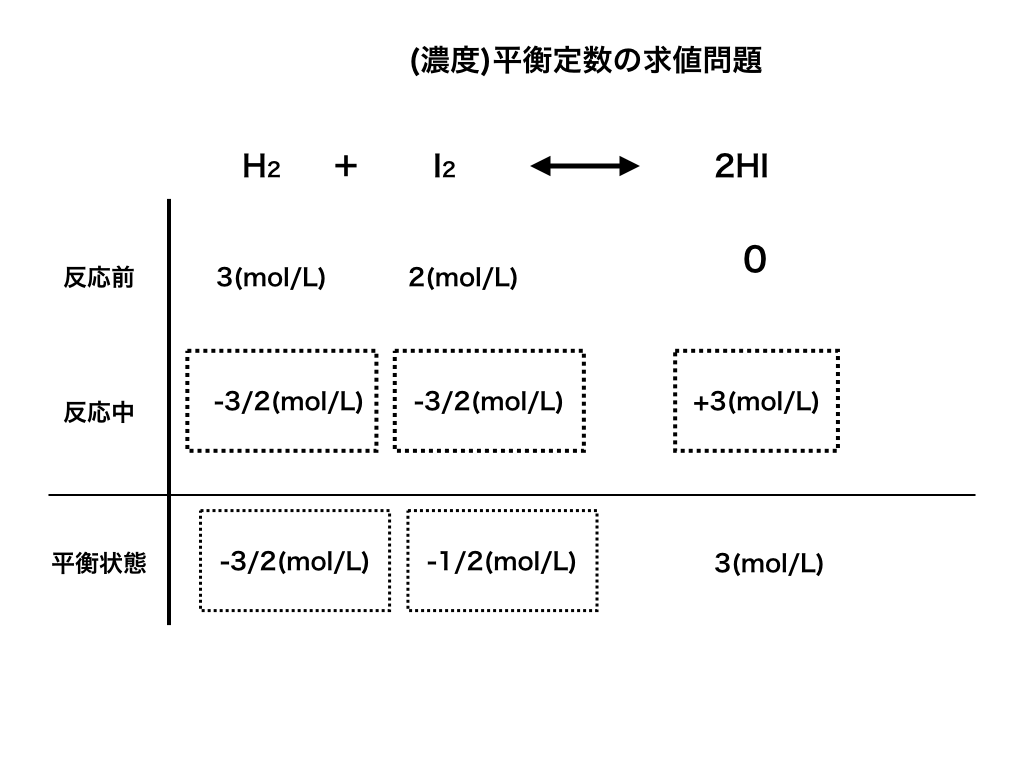
上の表の通り平衡時のモル濃度を計算して、Kcの式に代入していくと、

$$Kc=\frac{(3(mol/L))^{2}}{1.5(mol/L)\times 0.5(mol/L)}$$

分子の単位が(mol/L)の二乗、分母の単位も(mol/L)・(mol/L)なので、きれいに単位が打ち消しあって、この場合の平衡定数は単位がない”無次元数”となります。

よって、上の計算の結果\(K_{c}=12\)・・・（答）

Kcを求めたあとに頻出の問題と解法

実際にこのような手順を踏んで（濃度）平衡定数を求めた後は、これを利用する問題が続く事が一般的です。

例えば、『問題２の平衡状態で温度が変化していない容器にヨウ素（など）を●(mol)加えた。この後、再度平衡状態となった時の、I_{2}、H_{2}、HI それぞれの物質量を答えよ。』

といったものです。

ここでは、『温度』が変化していない事が大切で、平衡定数は温度による影響しか受けないので先ほど求めたKcがそのまま使えます。

ゆえに、”Kc＝12”のままで同じです。

問題２と同様に前・中・平衡（再度）の表を描き、変化した分を文字で置いて→$$12=\frac{(HIのmol濃度)^{2}}{(Iのmol濃度）（H_{2}のmol濃度)}$$

をそれぞれ代入する事で各物質のmol濃度が求まります。

KpとKcの相互変換【重要！】

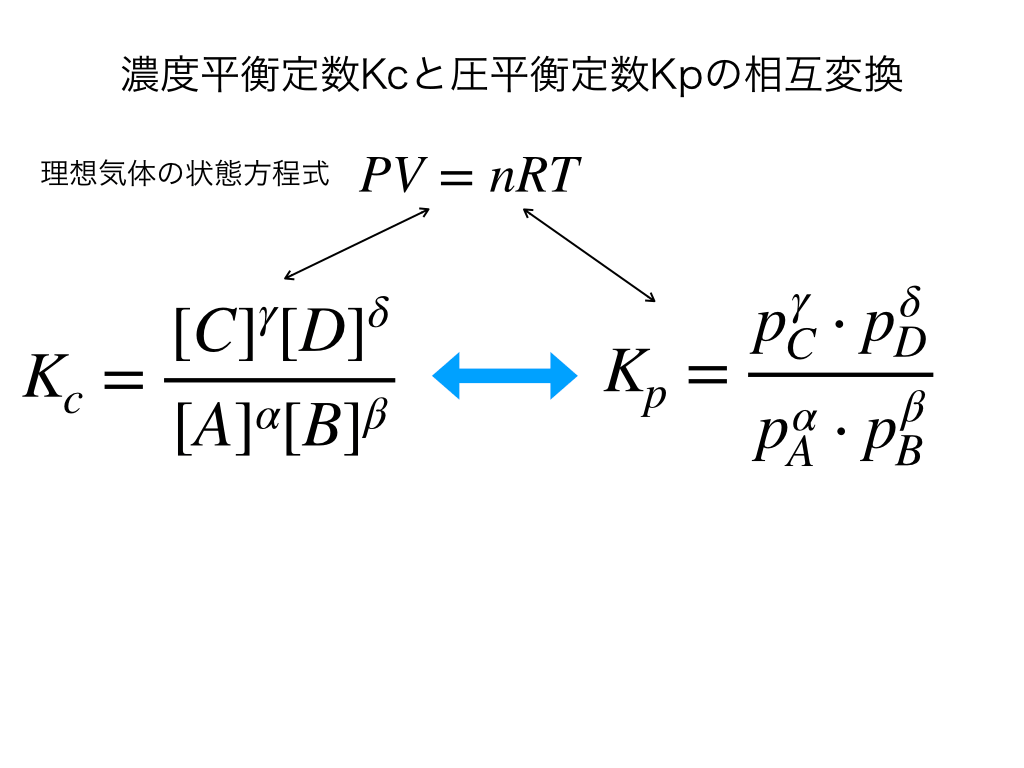
ここでは、”Kp”と”Kc”それぞれの定数を『理想気体の状態方程式』PV=nRTを媒介として、結びつける(変換する)方法を解説します。

$$Kc=\frac{(\frac{n_{C}}{V})^{\gamma}(\frac{n_{D}}{V})^{\delta}}{(\frac{n_{A}}{V})^{\alpha}(\frac{n_{B}}{V})^{\beta}}$$

解説と状態方程式を経由するイメージ図

（詳細は→『理想気体の状態方程式とボイル、シャルルの各法則』を参考にして下さい）

解説(Kp⇔Kc)

PV=nRTを変形すると、$$\frac{P}{RT}＝\frac{n}{V}$$となって、右辺が濃度平衡定数の式における[X]にあたります。

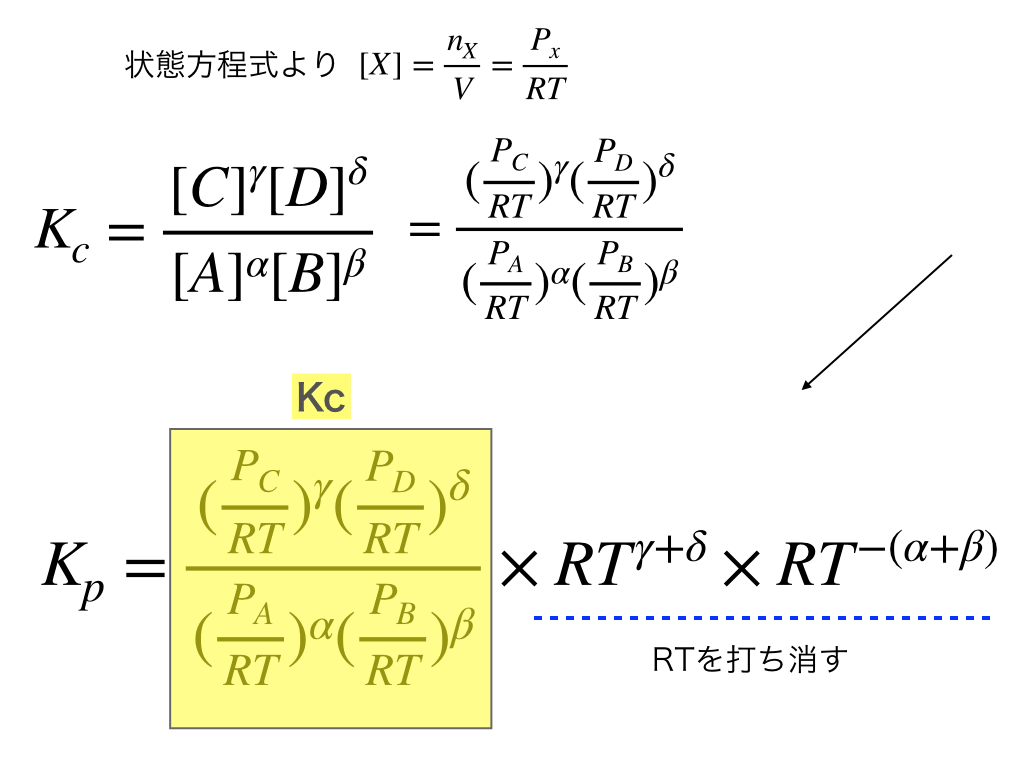
ゆえに、上のイメージの様にKcの式に、分母・分子にかかる余計なRTかけてを打ち消すと圧平衡定数Kpが求まります。

今回のまとめと関係する記事

今回は、Kc（濃度平衡の復習）からKp（圧平衡定数）の求め方と例題、KcとKpの変換・単位について解説しました。

理論化学の中でも化学平衡は「超重要分野」なので、ぜひ何度も復習してみてください。

次回は”反応速度と平衡の関係・『”係数乗”は【反応速度】では普通成り立たない理由』”について解説していきます。

〜気体分野と電離平衡へ〜

「化学平衡の基礎知識と問題(1)」

「(今ココです)Kp:圧平衡定数の求め方(2)」

「反応速度(定数)kと化学平衡(3)」

平衡と酸・塩基との融合は

＞＞「電離平衡と弱酸のpHの求め方」

平衡がかたよるor変わらないルールは

＞＞「ルシャトリエの原理と注意が必要な『希ガスの注入』」

今回も最後までご覧頂き、ありがとうございました。

「スマナビング！」では、読者の皆さんのご意見・ご感想の募集をコメント欄で行なっています。  

また、お役に立ちましたら、snsでB！やシェアをしていただけると励みになります。

・お問い合わせ/ご依頼/その他ご連絡は、【運営元ページ】よりお願いいたします。