
これで解ける!単振動
力学最後の壁、かつ、波動、電磁気にもつながる高校物理最重要単元「単振動」。
難しいですが、0から手順を踏んで丁寧に説明していきます。
ぜひ何度も読み返して、手を動かしてマスターして下さい!
尚、ハイレベル生向けの単振動は以下より。
(2019/11/17:等加速度運動の基礎記事を追加しました)
(2019/04/17:数学3の微積関連記事を追加しました)
目次(タップした所へ飛びます)
単振動を学ぶステップ一覧
基礎編
step0ー1:はじめに
step0ー2:等速円運動のおさらい
step0ー3:単振動の式
step0-4:図で理解する単振動の式
step0 ーα:微分で全てが繋がる
step0ーβ:数学Ⅲ未習者向けの数学的準備
step0ーγ:実際に微分してみよう!
問題編
step1:正方向を決めて軸を書く
step2:物体にかかっている力を全て書き出す
step3:運動方程式ma=Fを、a=−◯xの形へ変形する
step4:周期T、振動中心X0、振幅を求める
単振動(基礎:仕組みの解説編)
ここでは、単振動を0から学ぶにあたって必要な前提知識から、実際に微分を使わずに単振動の式を図を使いながら導出します。
後半部分では、数学3が未習の人にも分かるような簡単な微分の解説と、微分を最低限利用することで単振動の式がかなり楽に導けることを示します。(必ずしも微分を使う必要はありません)
step0ー1:はじめに
「等速円運動の正射影が単振動」という風に教科書等に書かれているかと思います。
難しそうなフレーズですが、等速円運動している物体に光を当てた時、後ろには影がうつります。
その影の動き=単振動 と言っているだけです。
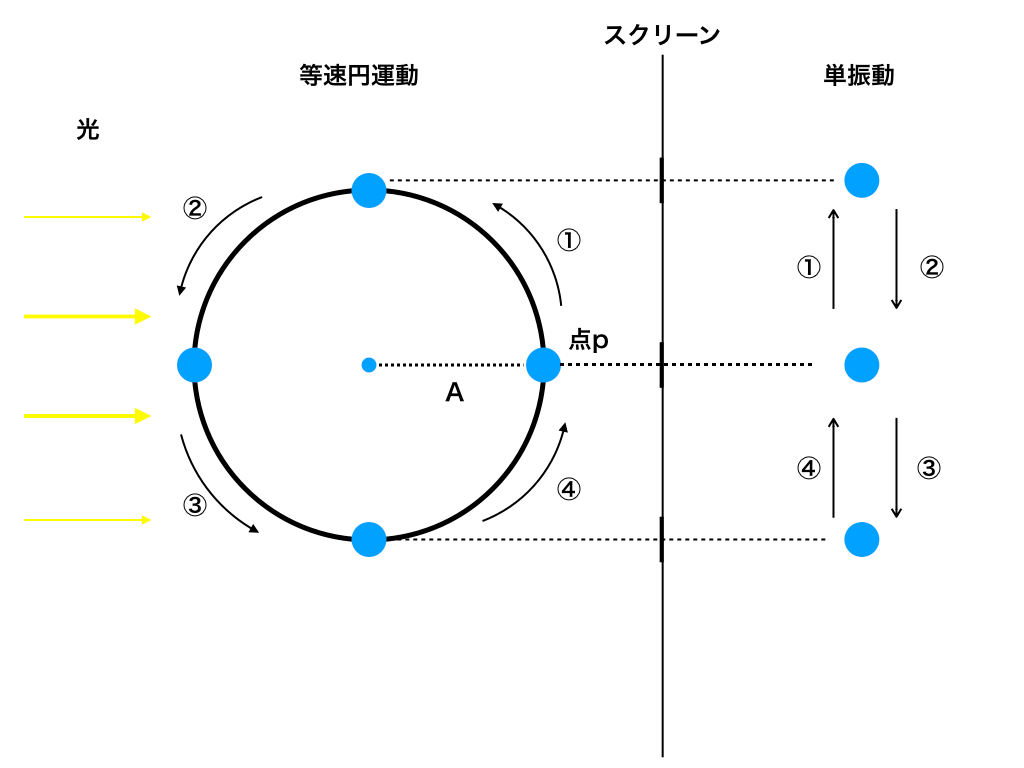
単振動と聞いただけで身構える人も多いですが、単純な振動(simple harmonic motion)なので、
ひとつひとつ確認しながらついて来て下さい。必ずできるようになります!
step0-2:等速円運動のおさらい
その名の通り同じ速度で円の周上を動く運動です。
等速円運動をしている物体には向心力と言う力が円の中心方向に常にかかっています。
もし向心力が無いと、円周上から飛び出してしまいます。
また、等速円運動では、角速度ω(rad/s)と言うものが登場します。
単位を見るとわかりますが、1秒当りに何ラジアン(rad)円周上を進むか?と言う意味です。
詳細は>>「等速円運動の基本と”向心力”・”遠心力”」をご覧ください。<<
これまでの速度v(m/s)および加速度a(m/s^2)の対応を見てみます。
円の半径をA(m)とします。
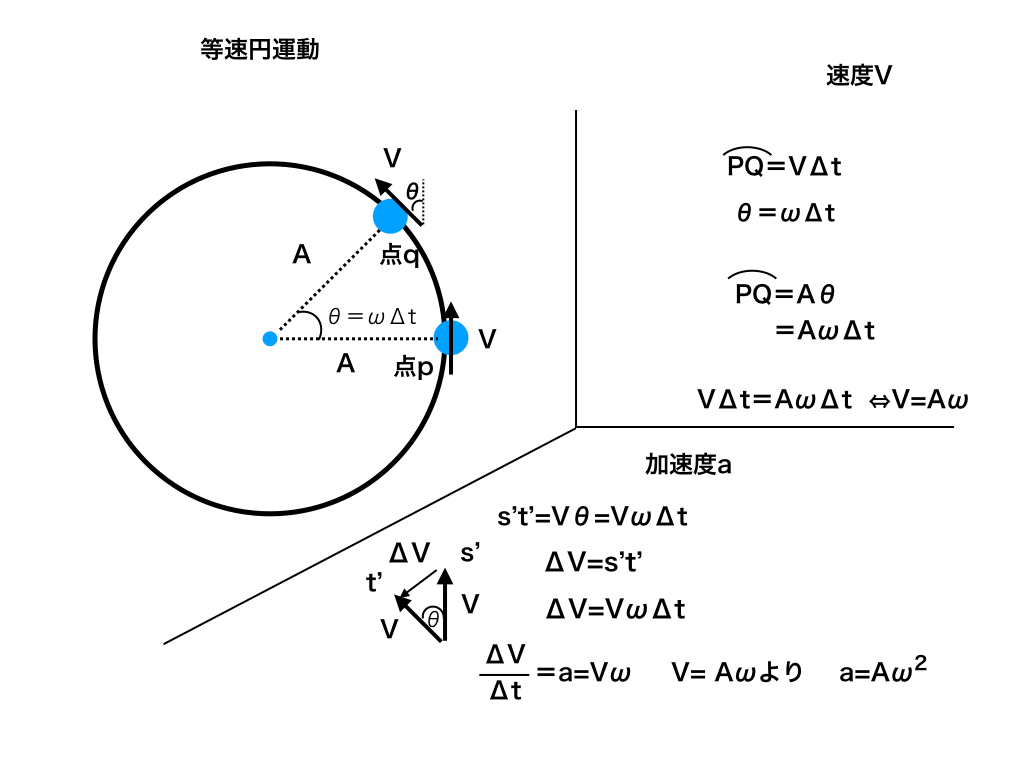
今図の様に、円周上の点pから点qまでΔt(s)で物体が進む時、
弧pqの長さはVΔt、また回転した角度θ=ωΔt、弧pqはAθとも表すことができるのでVΔt=AωΔt
,両辺Δtを割ると,V=Aωが導けます。
$$\begin{aligned}V\Delta t=A\omega \Delta t\\
V=A\omega \end{aligned}$$
つまり速度=半径×角速度が言えました。
次に加速度について見ていきます。点pでの速度と点qでの速度を取り出すと図1-2の様に
Vの変化ΔV=弧s‘t’になります。弧s‘t’の長さは、Vθ=VωΔt
従って、ΔV=VωΔt
ここで、加速度a(m/s ^2)は速度÷時間だったので、ΔV/Δt=Vω
∴ a=Vω=Aω^2
$$a=\frac {\Delta V}{\Delta t}=Vω =A\omega^{2}$$
このstep0-2で出て来たV=Aωとa=Aω^2は単振動を学ぶ上でも非常に大切な式なので、導き方も含めてしっかり身につけておいて下さい!
step0-3:単振動の式
ここでは、単振動を学ぶ時避けて通れない式を並べます。
三角関数も入って難しそうにみえますが、等速円運動をしっかり身に付けていれば、
理解出来るので安心してください!
これらの式は、問題文から一度作っておくと、時間(t)に任意の数字を代入するだけで、
その時の単振動している物体の位置/速度/加速度を求めることが出来ます。
(今シリーズで段階的に詳細は説明して行きます)
位置x
\(x=A\sin\omega t\)
速度v
\(v=\omega A\cos\omega t\)
加速度a
\(a=-\omega^{2}A\sin\omega t\)
ここで、\(A\sin\omega t\)は=x(位置)
を加速度の式に代入すると、
\(a=-\omega^{2}x\)・・・最重要の式です!
但し、式中の文字の意味と単位は次の通り
xは変位(m) 、vは速度(m/s)、aは加速度(m/s2)、ωは角速度(rad/s)、Aは振幅(m)
step0-4:図で理解する単振動の式
では上の4つの式を等速円運動を用いて導いていきます。
<図2>の様に、速度v‘で等速円運動する物体を横から光を当てます。
物体が点pから点qへ(θ=ωt)だけ動いた時、その影はA sinωtだけ上向きに移動しています。
これが、x=A sinωt の式の意味です。
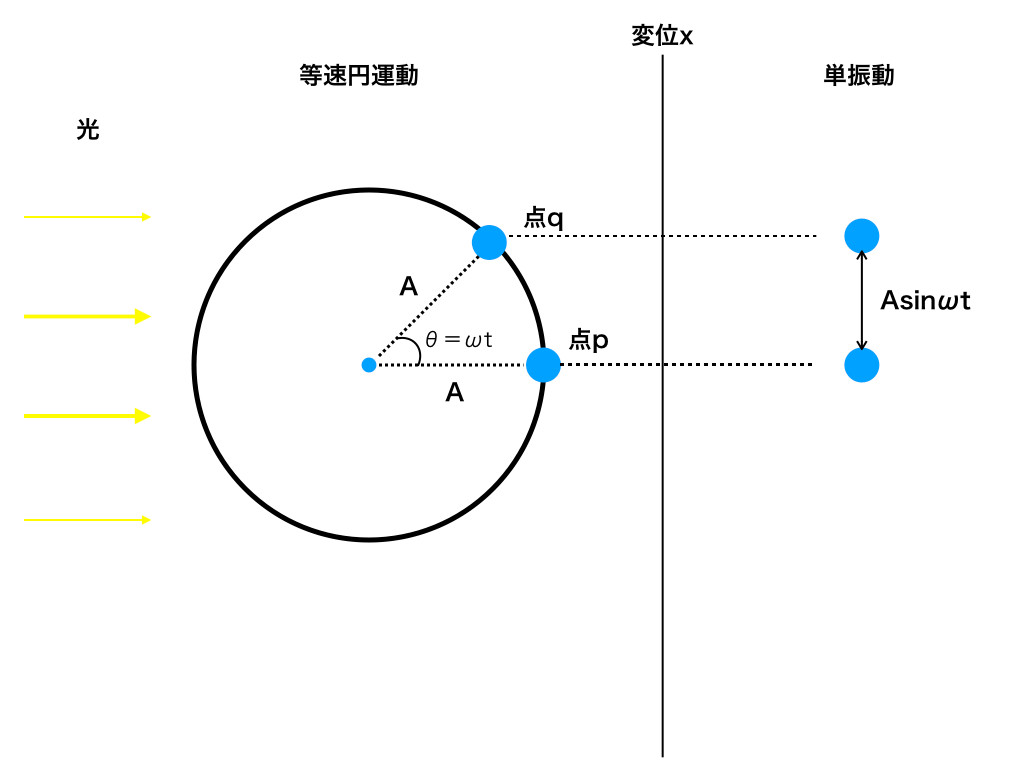
<図2:単振動と等速円運動の変位x>
次に図3の様に、点pqを物体が移動する時、点qでは円の接線方向に速度v’で物体が進んでいます。
これを横から光を当てて、その影を見ると、v=v‘cosθ、かつ、θ=ωtより、影(単振動)の速度v=v’cosωt
ここでv‘=Aωだったので(step0-2参照)
v=Aωcosωt
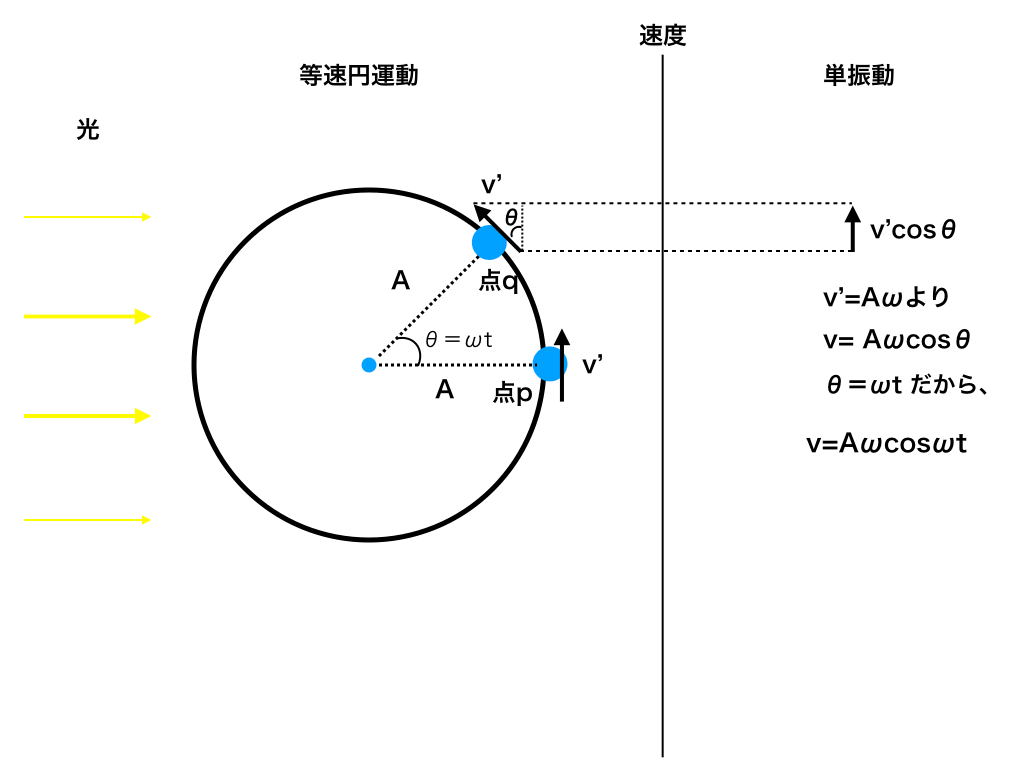
<図3:単振動と等速円運動の速度>
最後に図4の様に等速円運動の加速度は、
常に中心を向いていて、その大きさはa’=Aω2(step0-2参照)より
その加速度運動する物体の影:単振動にの加速度は
a= ーa‘sinωt ⇔a=ーAω2sinωt
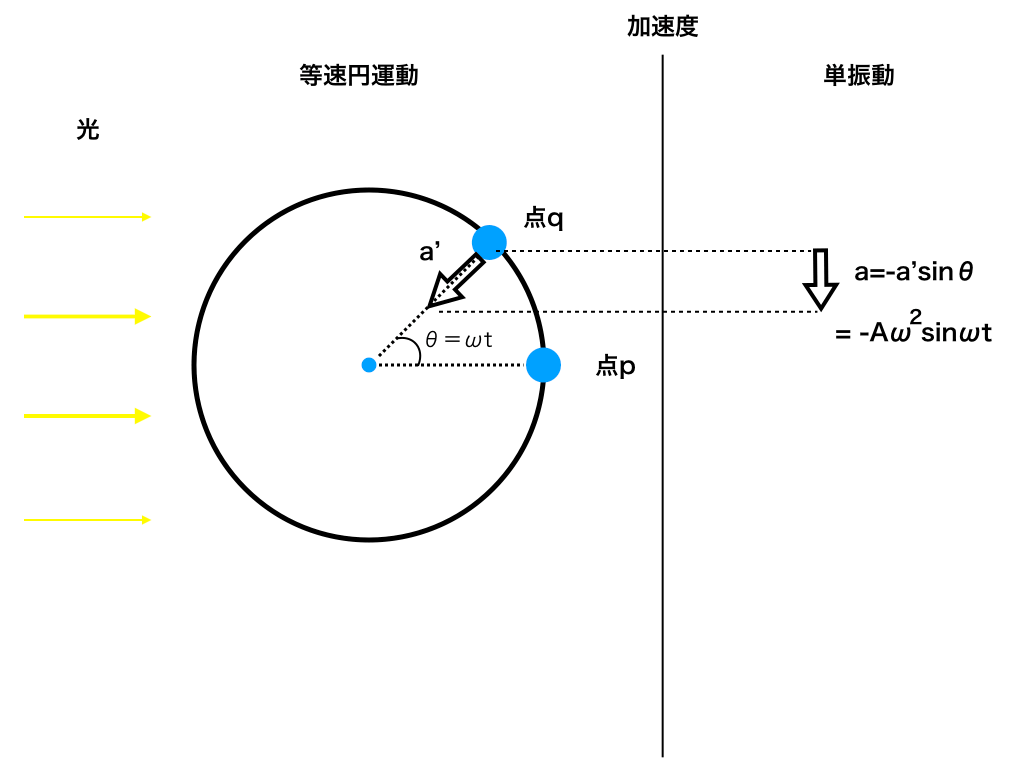
<図4:単振動と等速円運動の加速度>
これで全て等速円運動の図から単振動の式が導出出来ました。
ちなみに、”a=ーAω^2sinωt”の”A sinωt”の部分は”x=A sinωt”と同じなので、置き換えて、
\(a=ー\omega^{2}x\) とすることができます。(これは先ほども出てきました)
step0ーα:微分で全てが繋がる
上で整理した式は、高校範囲の微分(数学Ⅲ)で簡単に導出できます。こちらの方が本質的なので、是非理解しておいてほしいです。
step0 ーβ:数学Ⅲが未習の人向けの準備
数学Ⅱの微分では、微分する対象はxなどの一変数多項式(例:\(x^{2}+5x+6\))でしたが、
数学Ⅲではsinやcos、logなどいろいろな関数を微分します。
この記事ではあくまでも単振動の式を理解する事を目的にするので、以下の事を知っておいてもらえれば十分です。
三角関数の微分
\(\sin x\)をxで微分すると\(\cos x\)
\(\cos x\)をxで微分すると\(ー\sin x\)になる。
合成関数の微分
合成関数とは、関数の中に関数が含まれているもので、これを微分するときは注意が必要になります。
例)sin2x
はsin◯という関数と2xという関数を合成したものです。
これをxで微分するときは、まずsin◯をcos◯にして、2xを微分した2を係数として頭に付けます。
従って(例)の関数の微分は、(sin2x)‘=2cos2x となります。
step0-γ:微分で単振動の式を導出する
図で確認したx、v、aの式を微分で考えてみましょう。
v(速度)はxーtのグラフの傾き=x(変位)をt(時間)で微分したものです。
また、a(加速度)はvーtグラフの傾き=v(速度)をt(時間)で微分したものです。
x=A sinωt をtで微分すると、x‘=v
(sinωt)’=ωcosωtとなるから、x‘=v=ωA cosωt。
更にvをtで微分して
( cosωt)’=ーωsinωt より、v‘=a=ーω^2A sinωt。
ここで、a=ーω^2A sinωtの
A sinωt部分は=xだから、置き換えてa=ーω^2xも成り立つ。
確かに、step0-4の図で確認した通りになりました!
この様に微分を使う方が本質的で役に立つことも多いので、理系/医系を目指している人は、独学でも早めに数学Ⅲを勉強する事をお勧めします。
(このサイトでも独学をフォローするコンテンツを提供していきます!)
#2018/06/05追記|数学Ⅲのコンテンツを追加しました。
>>2019/04/17追記:「数学Ⅲの微積分の解説記事総まとめ」/「これから数3を学ぶ人向けの予習・復習記事」<<独学用数学3の記事まとめへのリンクを追加しました。
単振動の問題編
長い単振動の解説が終わり、いよいよ問題編に入ります。
基礎編がしっかり理解できていることを前提に、例題を通して解法プロセスを紹介して行きます。
(例題)図5の様に質量mの物体Aが、自然長L0、バネ定数kのバネにつながれている。
この時Aを右方向へxだけ引っ張った。その際の単振動の周期T、振動中心x0、振幅を求めよ。
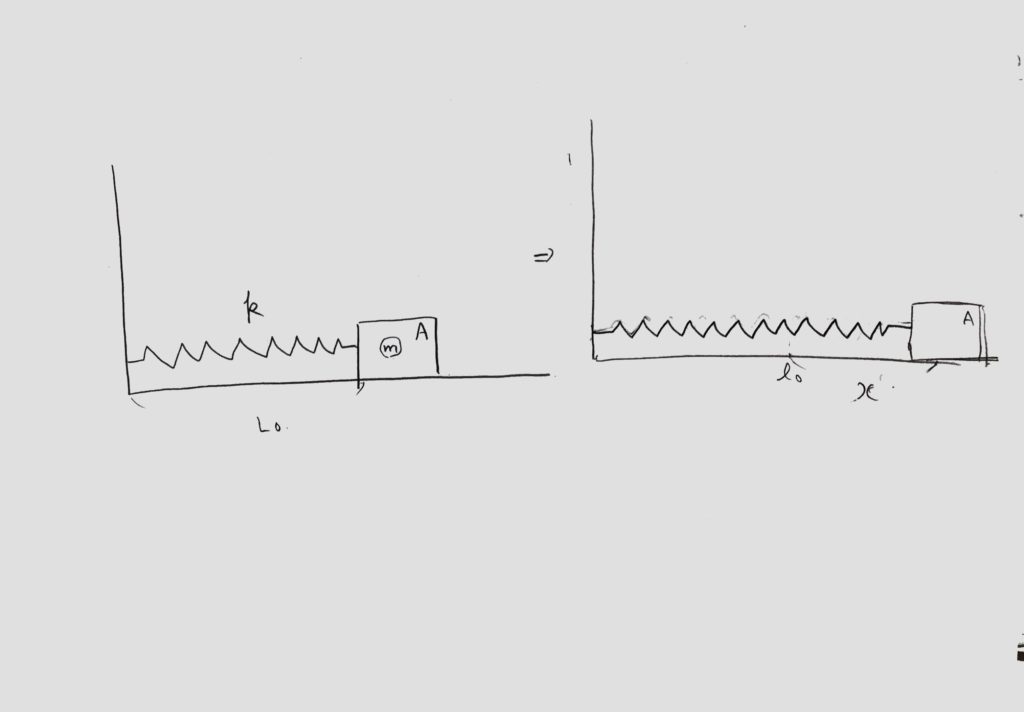
<図5>
step1:力学は軸が全て!軸を定めよう。
問題文には特にどの方向が正と書いていないので、自分で軸を定める必要があります。
今回は右向きを正、原点Oを物体Aの最初の位置とする軸を定める事にします。
step2:物体にかかっている力を全て書き出す
物体Aには重力mg、垂直抗力N、バネの復元力kxがかかっているので図に書き込みます。
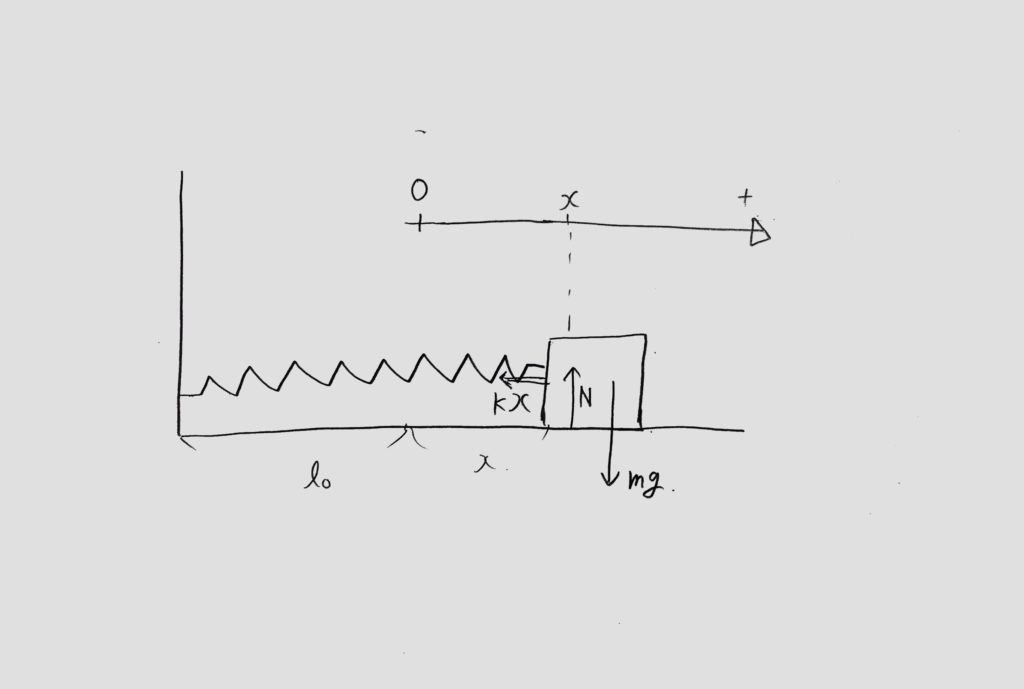
step3:運動方程式(ma=F)を書き、a=ー◯xの形に変形する。
運動方程式を立てるにあたって、鉛直方向の力は釣り合っており、今回は無視できます。
水平方向の運動方程式は、step1で右向きを正とする軸を定めたので、ma=−kx と書けます。
この式をstep0-4:の1番下の式「a=ー◯x」に変形して行きます。ma=ーkxよりa=ーk/m(x)
\(\begin{aligned}ma=-kx\\
a=-\frac {k}{m}x\end{aligned}\)
step4:いよいよ周期T、振動中心x0、振幅を出して行きます。
ここでa=−ω^2xと見比べて、\(\begin{aligned}a=-\frac {k}{m}x\\
a=-\omega^{2}x\end{aligned}\)
ω^2=k/m
\(ω^{2}=\Large{\frac {k}{m}},ω =\sqrt {\frac {k}{m}}\)
ω=√k/m と出来ます。周期T=2π/ωなので、$$T=\frac {2\pi }{\omega }( s) $$
T=2π√m/k
$$T=2\pi\sqrt {\frac {m}{k}}( s) $$
振動中心は加速度がゼロになる場所です。
今回はx=0でa=0となるので、元々の位置が振動中心になっています。
振幅は、xー原点なので、xとなります。
$$よって,x_{0}=0,A=x,T=2π \sqrt {\frac {m}{k}}$$
まとめと単振動の続編記事
今回はかなりボリュームがあったかと思いますが、
それだけ最重要の分野なので是非何度も読み返して「等速円運動」と「単振動」を得意にして下さい!
なお、次回は単振動問題編part2「摩擦力がかかる単振動」、「鉛直バネ振り子」等の少しレベルアップした問題を扱います。
単振動第1回「今ここです」
単振動第2回「単振動第二回:摩擦力が働く単振動の問題」
単振動第3回:「単振り子と近似計算を徹底的に解説!」
単振動第4回「浮力とは?そして単振動との融合問題」
を作成しました!最終更新日:2019年11月17日
今日もお疲れ様でした。お役に立ちましたらシェアをお願いします。
(後で読み返すためにPocketやはてなBook markがオススメです)

