数学Ⅲ:関数(二)【”合成”関数と”逆”関数】
<この記事の内容>:前回の無理、分数関数に引き続き、微分・積分でも重要な役割を担う「”合成関数”と”逆関数”」に付いて、ゼロから解説していきます。
<前回「”無理”関数・”分数”関数のグラフ・式と不等式の解き方をわかりやすく!」>
目次(タップした所へ飛びます)
合成関数とは
合成関数とは、一つの関数にもう一つの関数が入っている(イメージ的には、f(x)の"x"が別の関数に置き換わるような)ものです。具体的に見ていきましょう。
合成の例と記号の意味
具体例:\(f(x)=x^{3}+3x-2、 と、 g(x)=e^{x}\) を合成してみましょう。
(f⚪︎g)(x)と(g⚪︎f)(x)の順序と違い
さて、関数(ここではf(x)とg(x)の2つ)を合成する方法は2つあり、それぞれ記号が異なります。
1つ目は:(f⚪︎g)(x)
・・・これはf(x)のxにg(x)を入れたものなので、実際にこの合成関数を表すと、
\((f⚪︎g)(x)=(e^{3})^{3}+3e^{x}-2\)
2つ目は:(g⚪︎f)(x)
・・・こちらの場合はg(x)にf(x)を入れたものなので、同様に
\((g⚪︎f)(x)=e^{x^{3}+3x-2}\)
このように順序が異なるため、
基本的に(f⚪︎g)(x)=(g⚪︎f)(x)となることはありません。
”3つ”の関数の合成とその手順
さて、次は少々難易度を上げてf(x)、g(x)、h(x)の3種類の関数を”元”にした合成関数を考えてみましょう。
例題:次のような3つの関数を(f⚪︎g⚪︎h)(x)のように合成せよ。
これは二段階に分けて解きましょう。
\(f(x)=\frac{1}{x}\)
\(g(x)=\log{x+2}\)
\(h(x)=e^{x}\)
(STEP1)まずf(x)とg(x)を合成し、
$$(f⚪︎g)(x)=\frac{1}{\log{x+2}}$$
(STEP2)つぎにその合成関数とh(x)を合成する
ことで
$$((f⚪︎g)⚪︎h)(x)=\frac{1}{\log{e^{x}+2}}$$
ここで、logの底は"ネイピア数e"より分母の\(\log_{e}e^{x}\)を簡単にして、
$$(f⚪︎g⚪︎h)(x)=\frac{1}{x\log_{e}{e}+2}=\frac{1}{x+2}$$
と求まります!
(※):「合成関数の微分法をわかりやすく」
逆関数とは
(逆関数のイメージ)は、もととなる関数が「”単調”に(増加/減少)する」とき、xとyの1:1対応をx→yからy→xへと逆にしたものと言えます。(※:逆・合成関数の意味について詳しくは「写像:単射・全射・全単射」をご覧下さい)
具体例とグラフ・性質
最も有名な性質は『y=x』のグラフに関して、『元の関数と逆関数が対称になる』というものです。
これは、逆関数と元の関数のグラフを囲む”面積”を求めたり、グラフを図示する際に重要なhintsとなる事があるので、覚えておきましょう。
逆関数の求め方2ステップと注意点
では実際に、最も基本的で頻出の、\(f(x)=\log_{e}{x}\) 、の逆関数\( f^{-1}(x)\)を求める手順を2段階に分けて解説していきます。
(ちなみに、\(f^{-1}\)は”エフインバース”と言います)
step1:(x=)の形にし,xについて解く
y=f(x)として、\(y=\log_{e}{x}\)
「対数の定義(参考記事)」より、\(x=e^{y}\)
x=の形に変形して、\(x=e^{y}\)
step2:xとyを入れ替える
さて、xについて解き表せたので、x、yを入れ替えて、\(y=e^{x}\)
実際に\(f(x)とf^{-1}(x)\)のグラフを見てみましょう。
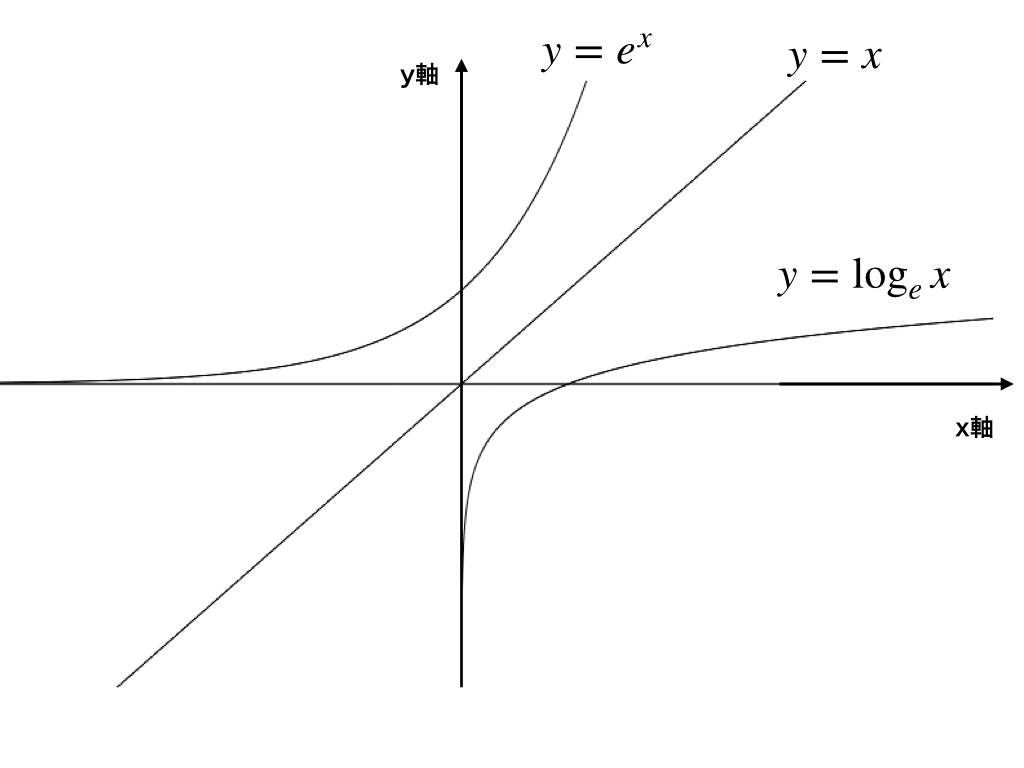
たしかに”y=xに関して対称”になることが分かります。
色々な関数まとめ
前回・今回で数学Ⅲで学ぶ「分数/無理/逆/合成」の各関数を紹介しました。
高校のカリキュラムでは、次に極限に進むので「極限の解説記事まとめ」を参考にしてください。(他の(二次)曲線や、微積分に付いては以下の項でまとめています)
分数/無理関数・微積・二次曲線へ
<前回>:「分数・無理関数のグラフと式」
最後までご覧いただきまして、有難うございました!
【学習メディア】スマホで学ぶサイト:「スマナビング!」では、読者の方のご意見ご感想の募集を行なっています。ぜひコメント欄迄お寄せください。
(※:ただいま個々の問題や、証明の質問等に関しては対応出来ない場合があります。)
・その他、お問い合わせ/ご依頼/タイアップなどにつきましては、【運営元ページ】よりご連絡下さい。

