
二次曲線シリーズ第2回:双曲線の特徴と式の導出
<今回の内容>:前回の「二次曲線と円錐の関係と『放物線』」に引き続き、今回は3つの二次曲線のうちの一つである”双曲線”の式の導き方と特徴を解説していきます。
双曲線とは
双曲線とは、円錐を上下に2つ重ねて斜めに切ると断面に現れる二次曲線で(図1参照)、その概形は下のグラフの通りです。
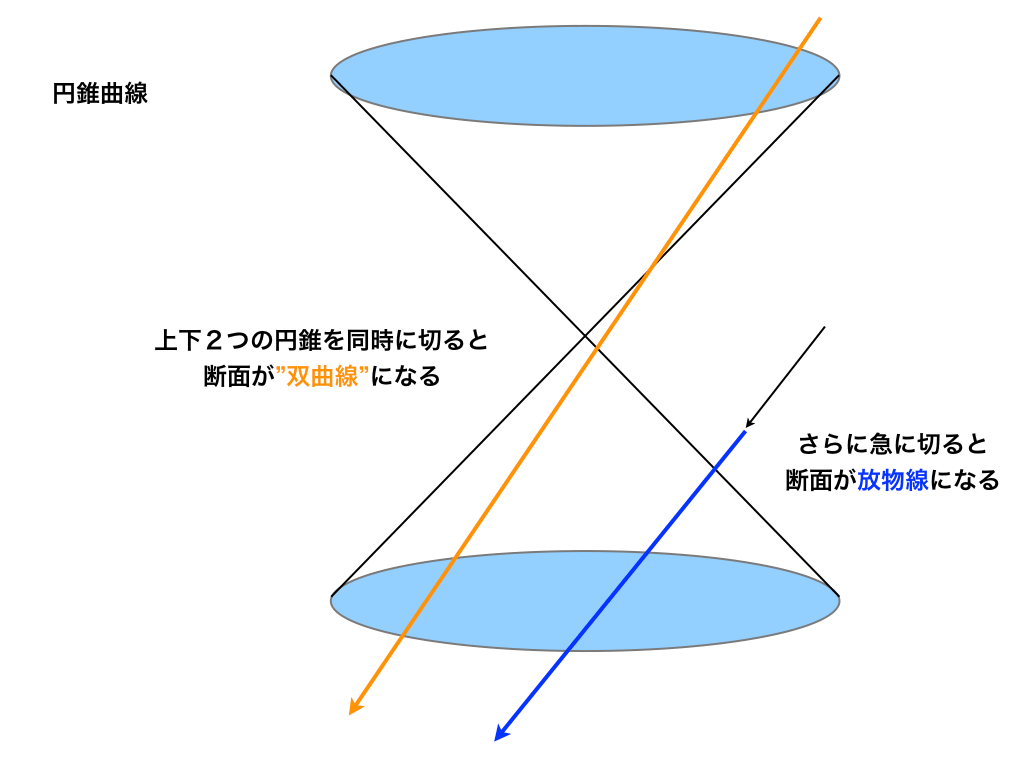
<双曲線と円錐(再掲)>
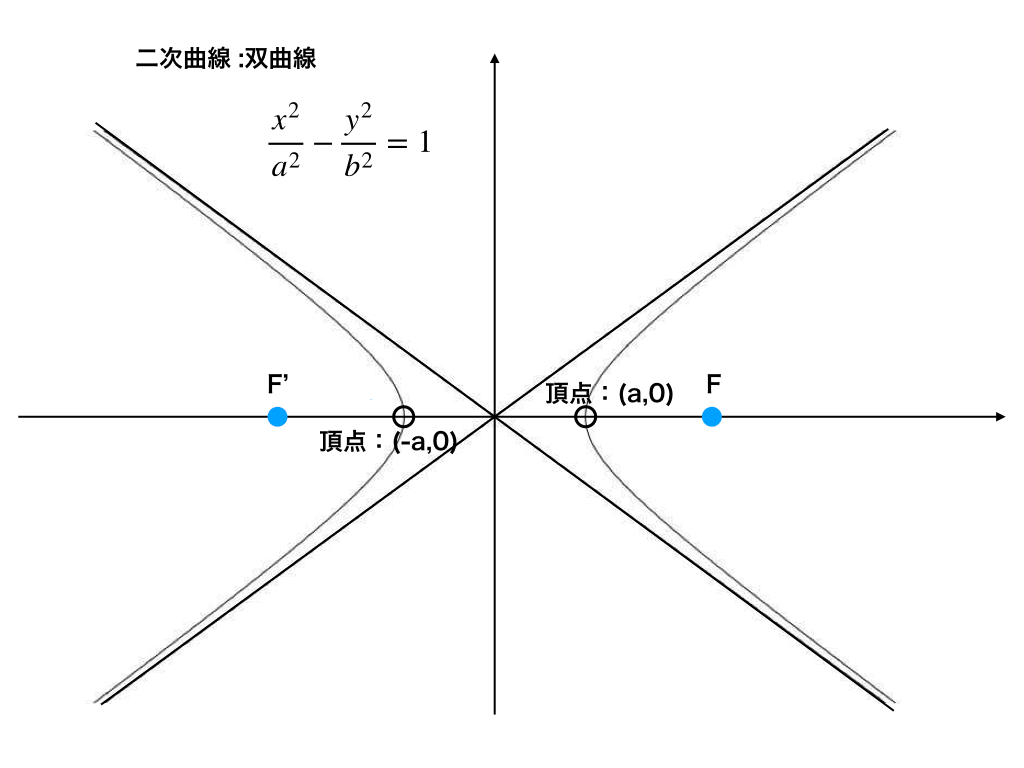
<双曲線のグラフ1>
双曲線の定義
双曲線の定義は、”焦点F”と”もう一方の焦点F'”の2点からの”距離の差が常に一定”である点(:ここではPとする)の軌跡ことです。(ただし、差が0の時を除きます)
双曲線の方程式の導出
では、この点Pの軌跡を導出することで双曲線の式を求めてみます。
まず、”一定の距離”を2aとします。
さらに焦点Fの座標を(f,0),F'の座標を(-f,0)とする(ただしf>a>0)と、PFとPF'の差が常に2aであれば良いので、『図形と方程式』の“軌跡の求め方”の要領で、Pを(x,y)とおくことで次の式が成り立ちます。
|PF-PF'|=2a
\(|\sqrt{(x-f)^{2}+(y-0)^{2}}-\sqrt{(x+f)^{2}+(y-0)^{2}}|=2a\)
ここで絶対値をとっているのは、PF<PF'の場合でも距離>0を取るためです。
上の式を変形していきます。
まず、絶対値を外した上で一方のルートを右辺に、残りを左辺に移行して2乗をすると、
\(\sqrt{(x-f)^{2}+(y)^{2}}-\sqrt{(x+f)^{2}+(y)^{2}}=\pm 2a\)
\((左辺)=\sqrt{(x-f)^{2}+(y)^{2}}\mp 2a\)
\((右辺)=\sqrt{(x+f))^{2}+(y)^{2}}\)
より、
\((x-f)^{2}+y^{2}\mp 4a\sqrt{(x-f)^{2}+y^{2}}+4a^{2}\)
\(=(x+f)^{2}+y^{2}\)
まだルートが残っているので、このルートの部分だけ右辺へ移項した上で式を整理していきます。
\((左辺)=(x-f)^{2}+y^{2}+4a^{2}-(x+f)^{2}-y^{2}\)
\((右辺)=\pm 4a\sqrt{(x-f)^{2}+(y-0)^{2}}\)
左辺は綺麗に打ち消しあって、\(a^{2}-fx=\pm a\sqrt{(x-f)^{2}+y^{2}}\)
となるので、もう一度ルートを外すために二乗します。
すると、\(a^{4}-2a^{2}fx+f^{2}x^{2}=a^{2}(x^{2}-2fx+f^{2}+y^{2})\)
ゆえに、\(a^{4}+f^{2}x^{2}=a^{2}x^{2}+a^{2}f^{2}+a^{2}y^{2}\)
ここから少し慣れが必要かもしれません。
(とりあえず次の項で紹介する『双曲線の式』を目指して変形していきます。)
\(x^{2}(f^{2}-a^{2})=a^{2}(f^{2}-a^{2})+a^{2}y^{2}\)
ここで、はじめにf>a>0だったので、\((f^{2}-a^{2})>0;で両辺を割ります\)
$$x^{2}=a^{2}+\frac{a^{2}y^{2}}{f^{2}-a^{2}}$$
これを更にaの二乗で割ることによって、我々が知っている双曲線の方程式にかなり近づきました。
$$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{f^{2}-a^{2}}=1$$
最後に、\(f^{2}-a^{2}=b^{2}\)(bは実数)と置くことで、$$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$$
となって、双曲線の式が導けました。
双曲線のグラフと式
上の項で導出したように、双曲線の式は$$\frac {x^{2}}{a^{2}}-\frac {y^{2}}{b^{2}}=\pm1$$で表されます。
(今回紹介したのは、右辺が1の双曲線でしたが、右辺が-1の場合も同様の考え方で導くことが可能です。)
焦点の座標
そして、その焦点の座標は、
・右辺=1の場合(すなわち以下の図1のように双曲線がx軸の正方向と負方向に開いている場合)\(F(\sqrt{a^{2}+b^{2}},0),F'(-\sqrt{a^{2}+b^{2}},0)\)
さらに
・右辺=-1の場合(今度は図2のように双曲線がy軸正・負方向に開いている場合)\(F(0,\sqrt{a^{2}+b^{2}}),F'(0,-\sqrt{a^{2}+b^{2}})\)
となります。
これは、はじめに焦点Fの座標を(f,0)としたので、\(f^{2}-a^{2}=b^{2}\)(bは実数)より\(f^{2}=a^{2}+b^{2}\)ここでルートを取ることによって、\(f=\sqrt{a^{2}+b^{2}}\)から求めることができます。

<双曲線のグラフ:右辺が1の場合>
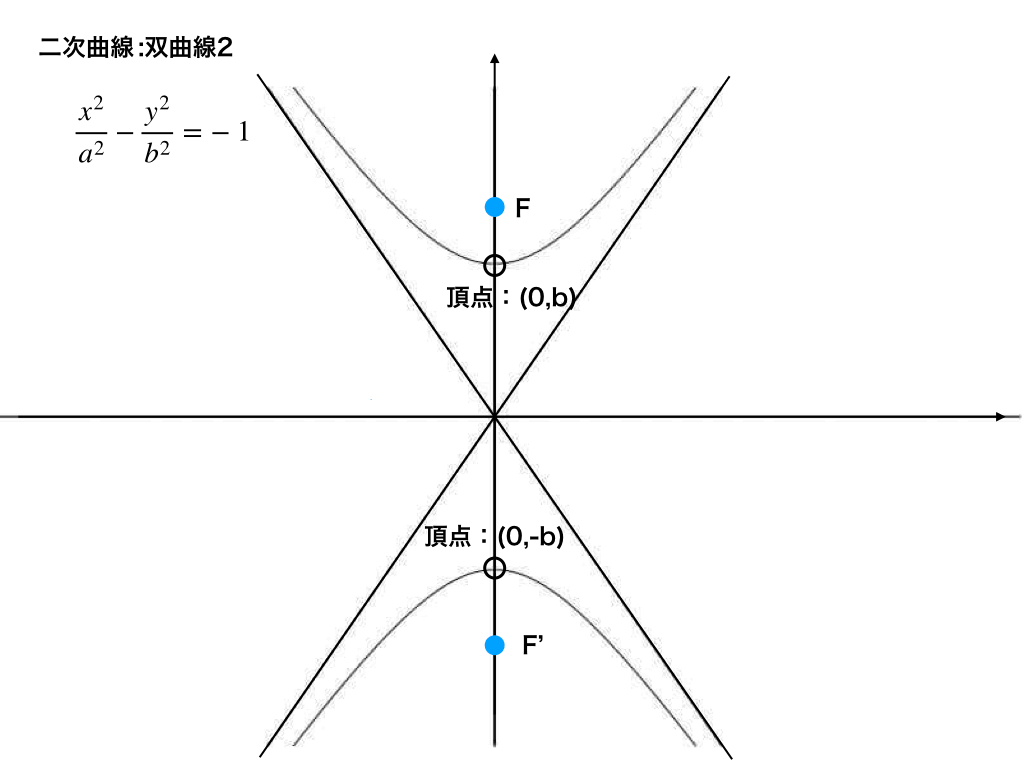
<双曲線のグラフ:右辺が-1の場合>
漸近線など双曲線の特徴
双曲線には、図にも書いていますが”漸近線”(読みは『ぜんきんせん』です)という直線が2本引けます。
これは、双曲線を伸ばし続けた時に限りなく近づく直線で、2パターンのうちどちらも$$y=\pm\frac{ax}{b}$$という式で表せます。
双曲線のまとめと次回「楕円」へ
・双曲線の定義は「2つの焦点の距離の差が一定の点の軌跡」である
・方程式/焦点/頂点はそれぞれ右辺の±1に応じて1つずつある
・漸近線は、どちらのパターンでも共通で「$$y=\pm\frac{ax}{b}$$」で表すことが出来る
次回は、3つ目の二次曲線「楕円」の式の導出・面積公式、接線の求め方について紹介していきます。
二次曲線シリーズと楕円へ
第1回:「二次曲線と円錐の関係と『放物線』」
第2回:「双曲線のグラフと方程式の定義・導出(今ここです)」
第3回:「楕円のグラフと式・面積公式と接線」
今回も最後までご覧頂き、有難うございました。
いいね!、B!やシェア、Twitterのフォローをしていただけると励みになります。
・その他のお問い合わせ/ご依頼に関しましては、お問い合わせページからご連絡下さい。

