
ベクトル方程式(空間ベクトル)の応用【平面の方程式と法線ベクトル】
この記事では、
・(直線の)ベクトル方程式の最小限の知識をもとに、
・苦手な人が多い「平面の方程式」の求め方、「空間ベクトル」の基本的な考え方について解説していきます
続編として、「法線ベクトルの求め方と空間図形への応用」を追加しました。
教科書や参考書でもベクトルの最後に扱われており、一度理解するまで少し大変かもしれません。
発展的な内容も扱いますが、つまずきそうな所にはイラスト&関連記事へのリンクを用意していますので、ぜひじっくりとご覧下さい。
目次(タップした所へ飛びます)
平面の方程式とは
まず「平面の方程式」とは何なのか?から解決していきましょう。
図形と方程式(数学2)のところで、「直線の方程式」について学んでいるかと思います。
これまでは、『y=ax+b』 の形で表していたものを、より一般化して『 ax+by+c=0 』と表すことによって、
傾きが無限大=y軸に平行な直線でも表すことができるようになったのでした。
今回学ぶ「平面の方程式」は、『ax+by+c=0』を文字通り“線“から”面“に変えた時、どのように表すかを考えます。
直線のベクトル方程式の復習
さて、ここで一旦直線のベクトル方程式について復習しておきます。
この「方程式」という名前が理解を余計に難しくするのですが、ベクトルで直線を表そうとするとどのようにすれば良いのでしょうか。
原点Oからある点A(a,b)へのベクトルをaとするならば、点Aを通るベクトル方程式は、方向ベクトルd(x ,y)と変数tを用いて、
l=a+td と表すことができました。
これは、以下の図1でもわかるように、原点から点AまでOAベクトルを使って、
残りの(傾き)を表す方向ベクトルd(青色のベクトルです)を利用することで、
点Aを通る直線lを全て表すことができるのです。
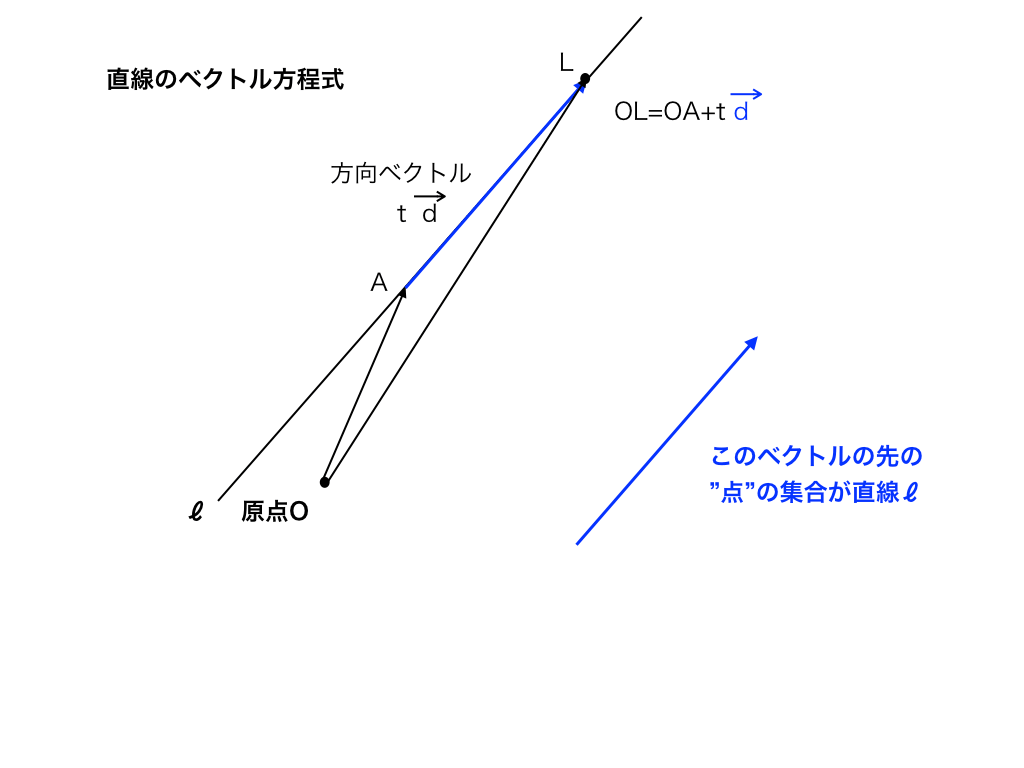
<直線のベクトル方程式の図>
(t=1,2,3・・・、-1,-2,-3・・・)と入れていくと方向ベクトルが伸縮して、
ベクトルの先の点が集まったもの=直線になることがわかるかと思います。
具体的に直線の方程式を導く
では、この直線のベクトル方程式から、直線の方程式を導いてみましょう。
つまり、ベクトルを利用せず、x、yの方程式で表すということです。
例題(0)
ベクトルl、a,dをそれぞれ成分で表すと、l=(x,y)、a=(3,5)、d=(2,5)である。
この時、直線のベクトル方程式から直線の方程式を求めよ。
解説(0)
この問題では、原点Oから点A(3,5)を通ってd上の点の集合が直線を表します。
したがって、(x,y)=(3,5)+t(2,5)
(x,y)=(3+2t,5+5t)より、x成分とy成分をそれぞれ連立して”t”を消去します。
x=3+2t・・・1*
y=5+5t・・・2*
(1*)×5:5x=15+10t
(2*)×2:2y=10+10t
よって、5xー2y=5
以上のように、t(媒介変数、パラメータと言います)を消去する事によって、図形と方程式で学んだ直線の方程式を導くことができました。
ax+by+c=0の形にすると、5xー2yー5=0 がこの問題の直線の方程式です。
法線ベクトル
ここで、空間ベクトルに移る前に、法線ベクトルについて簡単に解説しておきます。
法線ベクトルとは、ある直線ℓや、ある平面ρに垂直なベクトルのことを言います。
法線ベクトルと直線ℓや、平面ρ上とのベクトルの内積は0になります。<参考:「ベクトルの内積とは?」>
つまり、直線上や、平面上の一点と法線ベクトルが決まればその直線/平面の方程式が求まるのです。
実例とイラストを使って解説していきます。
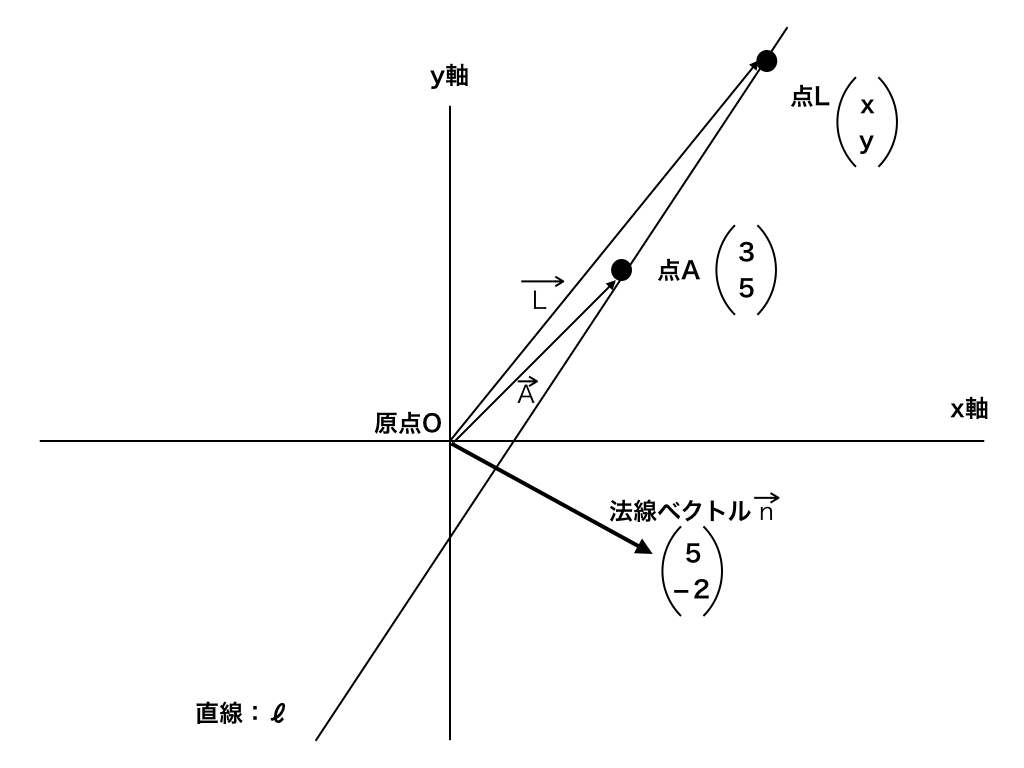
<法線ベクトルと直線>
法線ベクトルと直線上の点が「一つ」必要な理由
以下のイラストの通り、仮に点Aの情報がなく法線ベクトルのみしか分からなければ、
求めたい直線ℓに平行な直線が無数に存在してしまいます。
しかし、『点Aを通る』ということがわかれば、条件を満たす直線はℓのみになります。
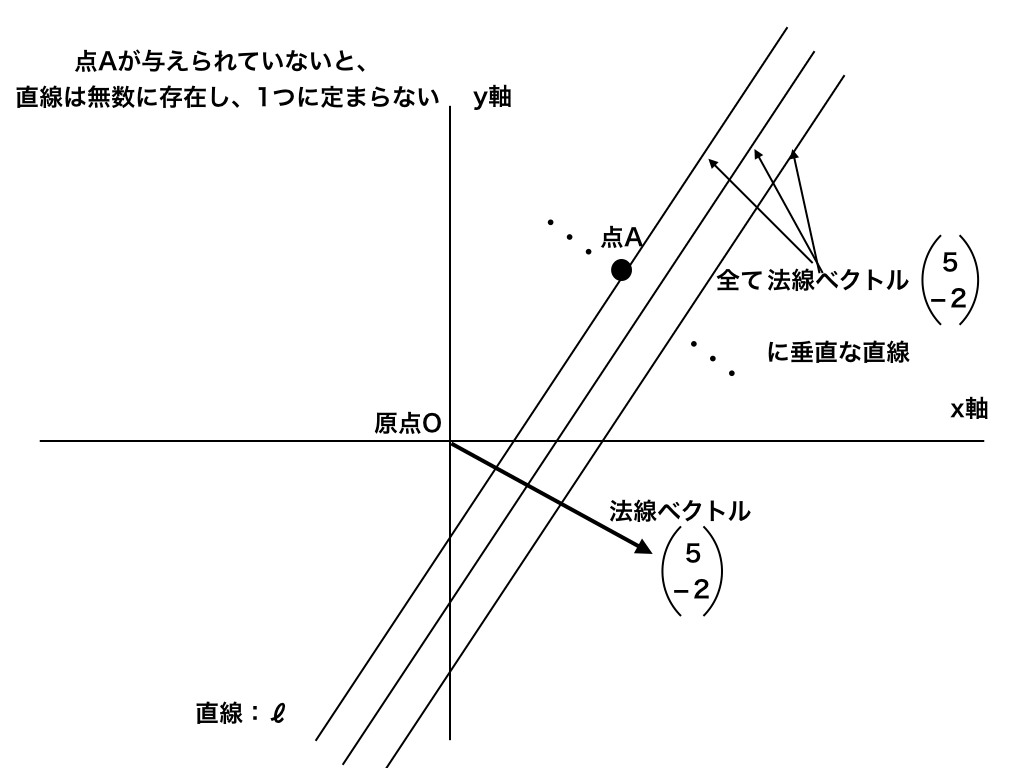
<直線と法線ベクトルの図>
直線から平面へ
では、いよいよ平面の方程式を導いていきましょう。
座標空間にある、平面の方程式を求めるときには3つの点の座標が与えられます。
(次回の演習編ではそれ以外の場合の問題を扱います:作成中)
ρをベクトルで表すには、一次独立(*)な2つのベクトルを用いる方法と、
法線ベクトルを利用する方法が主なのですが、後者の方が圧倒的に早く平面の方程式を導くことができます。
ただし、先に基本的なベクトル方程式を利用する方法から紹介していきます。
平面上の2つのベクトルから平面の方程式を導く
ここからは、平面の方程式を例題の形で解説していきます。(法線ベクトルを用いた解法は、下の「法線ベクトルから平面の方程式を導く
」を参照してください)
(問1):いまxyz空間に3点A(1,3,5)、B(2,1,4)、C(0,2,3)が平面ρ上に存在する。
この平面ρの方程式を求めよ。
解説
平面ρ上のどの点(ここでは点X;(x,y,z)とします)も、一次独立なベクトルABとACによって表すことができます。
つまり、係数に実数s,tを用いて、\(\vec {AX}=s\vec {AB}+t\vec {AC}\)とすることができ、
原点Oを基準にベクトルを分解すると、$$\vec {OX}-\vec {OA}=s(\vec {OB}-\vec {OA})+t(\vec {OC}-\vec {OA}$$
整理して、\(\vec {OX}=(1-s-t)\vec {OA}+s\vec {OB}+t\vec {OC}\)
これに、\(A=\begin{pmatrix}
1 \\
3 \\
5
\end{pmatrix},B=\begin{pmatrix}
2 \\
1 \\
4
\end{pmatrix},C=\begin{pmatrix}
0 \\
2 \\
3
\end{pmatrix}\)
\(とX=\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}\)
を代入すると、\(\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}=\left( 1-s-t\right) \begin{pmatrix}
1 \\
3 \\
5
\end{pmatrix}+s\begin{pmatrix}
2 \\
1 \\
4
\end{pmatrix}+t\begin{pmatrix}
0 \\
2 \\
3
\end{pmatrix}\)
これを整理すると、\(\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}=\begin{pmatrix}
1 + s-t \\
3 - 2s-t \\
5 - s-2t
\end{pmatrix}\)
となります。
あとはx=1+s-t・・・(1)、y=3-2s-t・・・(2)、z=5-s-2t・・・(3) 、の式中にあるsとtをうまく消してあげる事で、平面ρの方程式が導けます。
(少しややこしいですが、自分で導いてみてください。)
(解答):
(1)-(2)=-2+3s・・・(4)
2(1)-(3)=-3+3s・・・(5)
よって、(5)-(4): x+y-z+1=0・・・(答)
予備知識:一次独立(*)
一応、一次独立についてふり返っておくと、ベクトルa,bがある時それぞれのベクトルが平行、
もしくは重ならず、かつ、a,bがともに0ベクトルで無い事を、a,bが『一次独立』であると言います。
詳しくは以下の記事を参考にしてみてください。
法線ベクトルから平面の方程式を導く
直線の方程式を法線ベクトルと点Aを使って求めた時と同じように、平面の方程式も一点と平面の法線ベクトルから求めることができます。
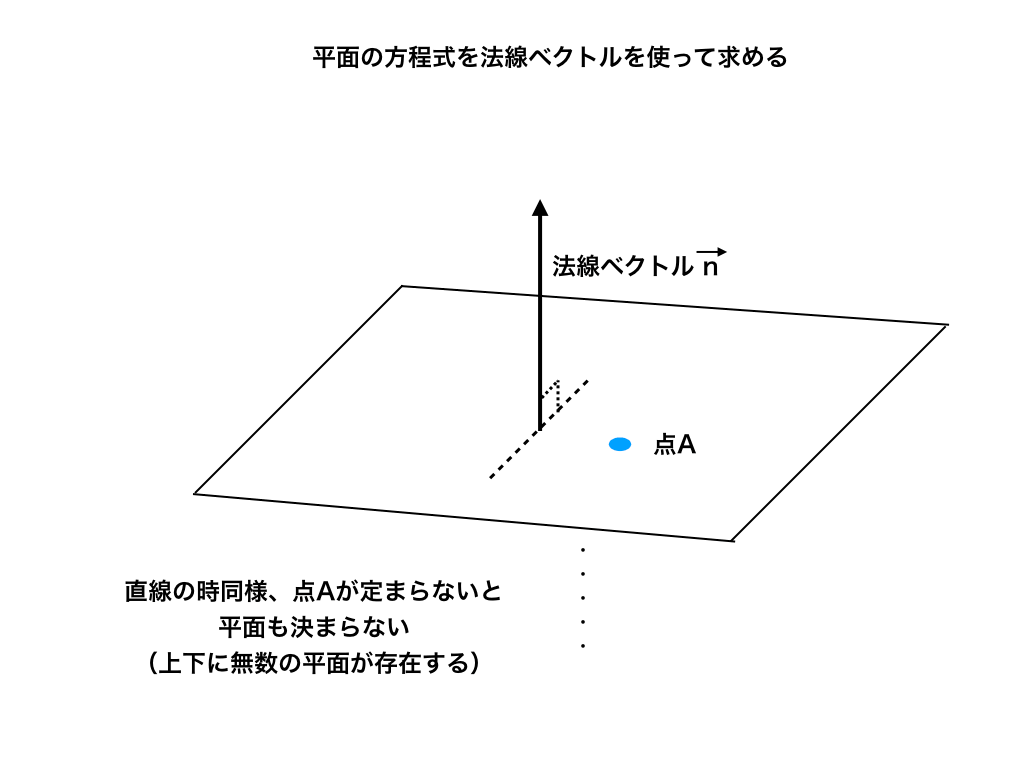
<平面と法線ベクトルの図>
なお、平面の方程式の場合も、<直線と法線ベクトルの図>と同じく、
求める平面上の点が1つ分からないと、求めたい平面ρに平行な面が無数に存在してしまいます。
(上<平面と法線ベクトルの図>参照)
法線ベクトルと外積
では、法線ベクトルが与えられておらず、平面上の点の座標が3つ与えられている時には、どうすればよいのでしょうか。
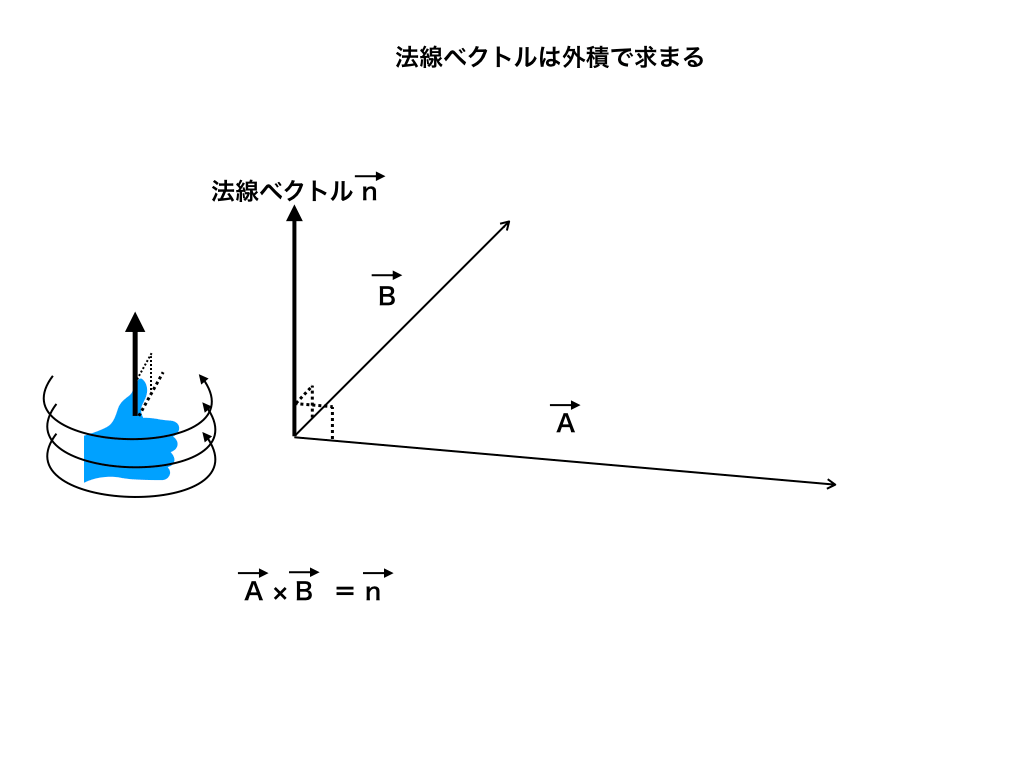
実は、高校範囲外ですが、ベクトルの外積を使う事によって、すぐに法線ベクトルを求めることが出来るのです。
これはテスト・入試でかなり役立つのでぜひ知っておいてください>>「ベクトルの外積の意味と求め方が分かる!」<<
この記事もいよいよクライマックスです!もう少しだけ読み進めてください。
(確認問題)いま、平面ρ上には3点:点A、点B、点Cが存在する。各点の座標は先ほどの問1と同じである。
この平面ρの方程式を(法線ベクトルを使って)求めよ。
解答解説
外積の求め方は理解できたでしょうか?
まず、ベクトルABとベクトルACの外積=平面ρの法線ベクトルn
なので、
\(\vec {AB}\times \vec {AC}=\begin{pmatrix}
1 \\
-2 \\
-1
\end{pmatrix}\times \begin{pmatrix}
-1 \\
-1 \\
-2
\end{pmatrix}=\begin{pmatrix}
3 \\
3 \\
-3
\end{pmatrix}\)
これにより、あっさりと\(\vec {n}=\begin{pmatrix}
3 \\
3 \\
-3
\end{pmatrix}\)が求まりました。
あとは、$$\vec {AX}と\vec {n}$$ の内積は0になる(垂直条件)ので、
\(0=\vec {AX} \cdot \vec {n}\)
\(=\begin{pmatrix}
x-1 \\
y-3 \\
z-5
\end{pmatrix}\cdot \begin{pmatrix}
3 \\
3 \\
-3
\end{pmatrix}=0\)
内積計算をすると、
0=3x-3+3y-9-3z+15
0=3x+3y-3z+3
よって、$$平面ρの方程式は、x+y-z+1=0 $$となりました。
x+yーz+1=0のグラフ↓
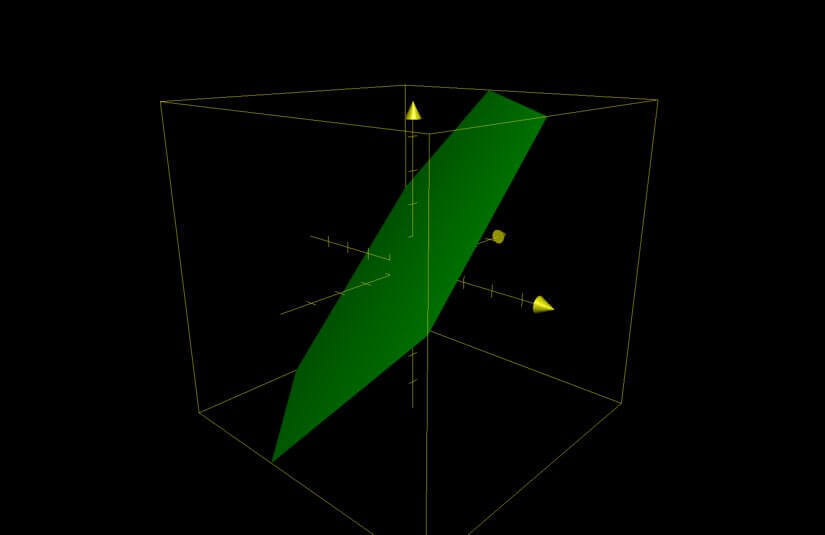
当然、先ほどと同じ結果になるのですが、
一次独立な2つのベクトルを変形し、パラメーターを消去した方法と比べてみてください。
法線ベクトル(外積を使って求める)を使う方法がいかに強力な解法かがわかるかと思います。
まとめとよく分かるベクトルシリーズ一覧
・平面の方程式の求め方は、パラメーター消去型と法線ベクトル利用型に分かれる。
・「外積」を知っておく事で、法線ベクトルが与えられていない時でも非常に楽に解くことができる。
・次回以降、「空間ベクトルの応用分野」の演習に入りますが、ぜひ何度も読み返して(できれば手を動かして)復習しておいてください。
空間ベクトルの応用分野:平面や球面の方程式シリーズ
第二回:>>「球面の方程式の求め方とその応用問題」
第三回:>>「2球面が作る円や接平面の方程式の求め方」<<
(NEW)第四回:「法線ベクトルと空間図形への応用」
>>>「ベクトルとは?苦手なベクトルを得意にする解説記事総まとめ」<<<
今回も最後までご覧いただきまして、本当に有難うございました。

