
ベクトル方程式を一から学ぼう
数学で苦手な分野を聞くと、必ず「ベクトル」があがってきます。更にその中でも「ベクトル方程式」は一・二を争う「よく分からん!」となる不人気範囲です。
この記事はそんな人に向けて、イラストを用いて「実は特別な物では無い」事を理解して貰うために作成しました。
※:2019/10/08「ベクトル方程式の”コツ”」を追加しました。
「媒介変数の消去」の項を追加しました。
※続編(「空間でのベクトル方程式」を作成しました。左のリンク、または『この記事のまとめの項』から続けてご覧ください。
途中で分からない用語等が出て来たら、これまでのベクトルの記事を集めた→「ベクトルシリーズ総まとめページ」で解決して、またこの記事に戻って来て下さい。
目次(タップした所へ飛びます)
ベクトル方程式とは
・「方程式」と「ベクトル」のおさらい
・ベクトル方程式
・直接のベクトル方程式
・円のベクトル方程式(定義)
・円のベクトル方程式解説part⑴→円のベクトル方程式解説part⑵
・媒介変数の消去による『ベクトル方程式⇔直線の方程式』の変換
・まとめ
方程式とベクトルのおさらい
「ベクトル方程式」に入る前に、「方程式」と「ベクトル」の意味をそれぞれチェックしておきます。
「方程式」とは数的な関係を等号で表した式を指します。そして「ベクトル」とは、「向き」と「大きさ」を持った(有向線分という)概念を指します。
またベクトルは、座標平面上の点に対応させたり、平面内に存在する「流れの向きと強さ」を表すことができます。
そして、ベクトルの関係は一般的に等号を用いて表すことができます。
従って、このことを考えると、ベクトルで構成されている式も「方程式」とみなすことが可能です。
これを「ベクトル方程式」と呼びます。
ベクトル方程式の具体的な使用法
高校数学では基本的な図形(直線、円、球、、、)をベクトル方程式で表現して計算する場面が多々あります。
※単位ベクトルとは?
「向き」は普通のベクトルと同様にありますが、「大きさ」が「1」のベクトルを単位ベクトルといいます。
簡単な例としてkを実数、eを単位ベクトル
$$として\vec {r}=k× \vec {e}を考えてみましょう。$$
これは日本語で書き表すと\(「\vec {r}は\vec {e}のk倍の長さを持つベクトル」\)
と言えます。このように、あるベクトルをもとのベクトルの関数のようにして表すことができるわけです。
直線のベクトル方程式
$$先ほど例として挙げた\vec {r}=k× \vec {e}$$
の意味をもう少し考えてみます。kを任意の値に取ってみると、
\(「\vec {e}の始点と終点を通る直線上のすべての点\)、
すなわち位置ベクトルを\(\vec {r}で表すことができる\)」ということがわかるでしょうか。
直感的に言うと\(\vec {e}\)の長さを\(k倍\)させて伸び縮みさせることで
終点を直線上にある点に一致させることができるという事です。
高校数学で扱う直線を表すベクトル方程式は、もっと一般化させて色々と表現することができます。
直線を表すベクトル方程式
点A,Bに対応する位置ベクトルを\(\vec {A},\vec {B}\)と書くとする。
点A,Bを通る直線上にある点Pに対応するベクトル\(\vec {p}\)は任意の実数をtとして
$$\begin{aligned}\vec {p}=t\vec {A}+\left( 1-t\right) \vec {B}\\
=\vec {B}+t\left( \vec {A}-\vec {B}\right) \\
=\vec {B}+t\overrightarrow {BA}\end{aligned}$$
上にある式の変形を逆の順番、つまり下から行って上の式を導出したとも解釈できます。
二つのベクトルの和が始点と終点を結ぶベクトルであることに注意すると、
三段目の式と\(\vec{A}-\vec{B}=\vec{BA}\)であることから、
一方の点Bから直線の方向と一致する\(\vec{BA}\)を伸縮させていることをこの式は表現していると言えます。
(ここでのBAの事を方向ベクトルという事が多くベクトルdで表し、tを任意の数として、ベクトルaを通る直線のベクトル方程式\(\vec{p}=\vec{a}+t\vec{d}\)とする事が多いです)
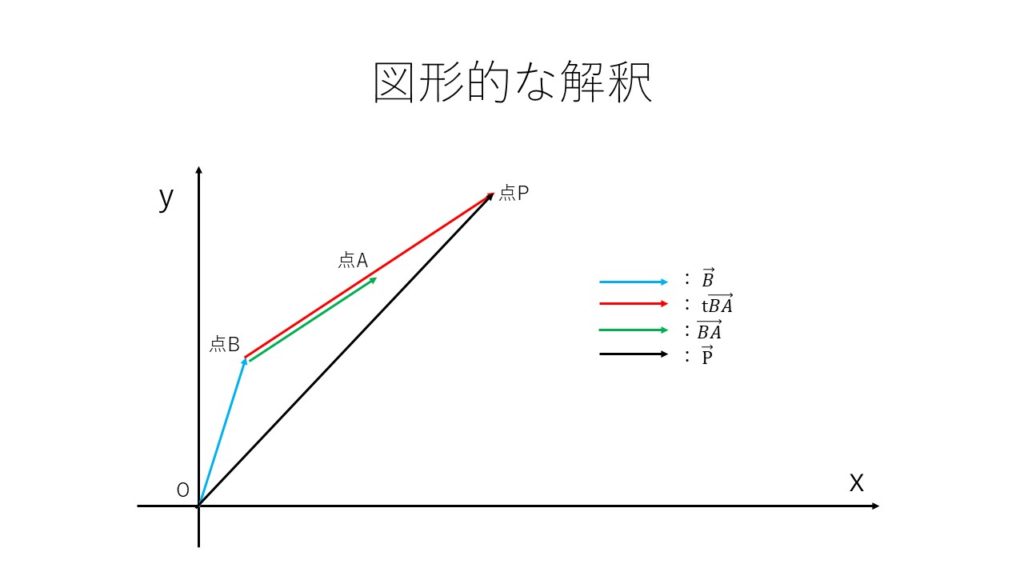
<図:直接のベクトル方程式の図形での解釈>
色で分けて考えると、「黒=青+赤、赤は緑のt倍の長さ」となることがわかります。
なお、もうひとつの考え方も存在し、内分点のベクトルを考えてみると、
点PがAとBの間にあるうちは一つ目の式を、「点A,Bをt:1-tで内分する点を表す式」と考えることができます。
これらのベクトル方程式の導出の考え方はxy平面上だけでは無く、xyz空間中でも適用することが可能です。
つまり、空間中に存在する直線を平面上と全く同じようにベクトル方程式として記述することができるのです。
「空間図形でも平面図形と同じ手順で解ける」のもベクトルの優位性の一つです。
円のベクトル方程式
次に、”円”をベクトル方程式で表すことを考えます。
半径rの円の中心をAとすると、円周上の点Pはベクトル方程式で\(| \vec {P}-\vec {A}| =r\)
即ち、$$| \overrightarrow {AP}| =r$$
と表すことができます。
※:関連する「図形と方程式(数2)での円」、「複素数平面(数3)上の円」もそれぞれ参考にしてください。
円のベクトル方程式⑴
上記のように、直線だけでなく、円もベクトル方程式で表現することができます。
式中のP→-A→は<図2>の赤いベクトルを表しています。ここで、\(| \overrightarrow {AP}| =r\)となるようにすると、点Aからrの距離にある点のみに点Pが対応するようになります。
平面上で、ある点から”等しい距離”に存在する”点の集合”は円以外にないので、
一つ目の式が”円を表すベクトル方程式”であることが理解できるかと思います。
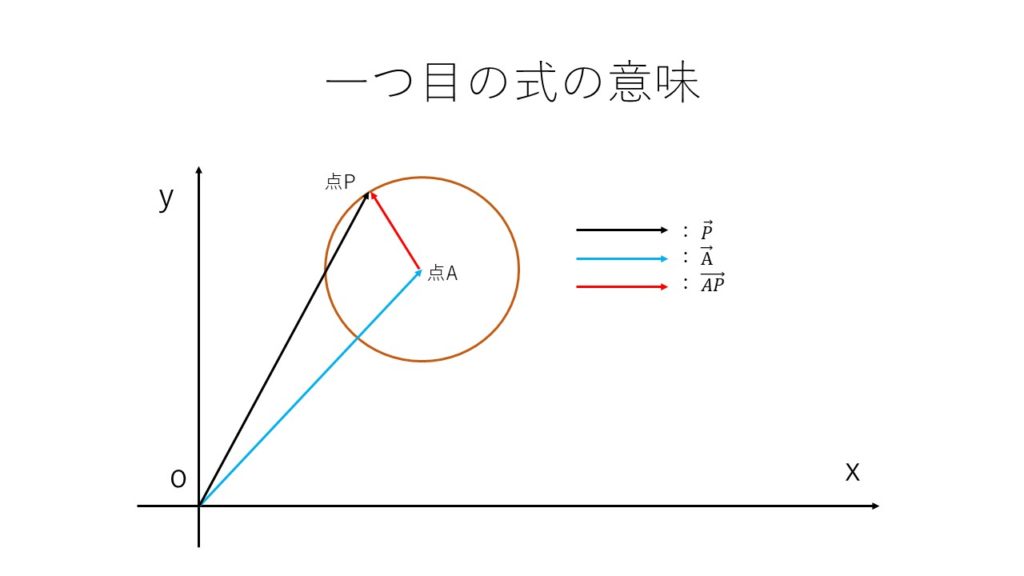 <図2:円のベクトル方程式の図形的な解釈>
<図2:円のベクトル方程式の図形的な解釈>
内積を利用した円のベクトル方程式⑵
次に二つ目の式を見てみましょう。この式の考え方は上の物とは全く違っています。
点A,Bを結ぶ直線を直径とする円のベクトル方程式は$$( \vec {P}-\vec {A}) \cdot ( \vec {P}-\vec {B}) =0$$
少々ややこしく、分かりにくくはなっていますが、
ここで注目すべきポイントは<図3>中の\(赤の\overrightarrow {AP}と黄色の\overrightarrow {BP}です。\)
点A,Bを直径の端とする円を考えて、さらに点Pをその円周上に置いたとき、
角度∠APBは円周角の定理によって90度であることがわかります。
ここで、互いに直交(90°)するベクトルの内積は0になります。
『(参照)ベクトルの内積と垂直条件』赤のAP→と黄色のBP→も互いに直交していることが分かったので、
$$\overrightarrow {AP}\cdot \overrightarrow {BP}=0 ⇔ \overrightarrow {AP}\bot \overrightarrow {BP}$$
これで、二つ目のベクトル方程式も確かに円を表すことがわかりました。
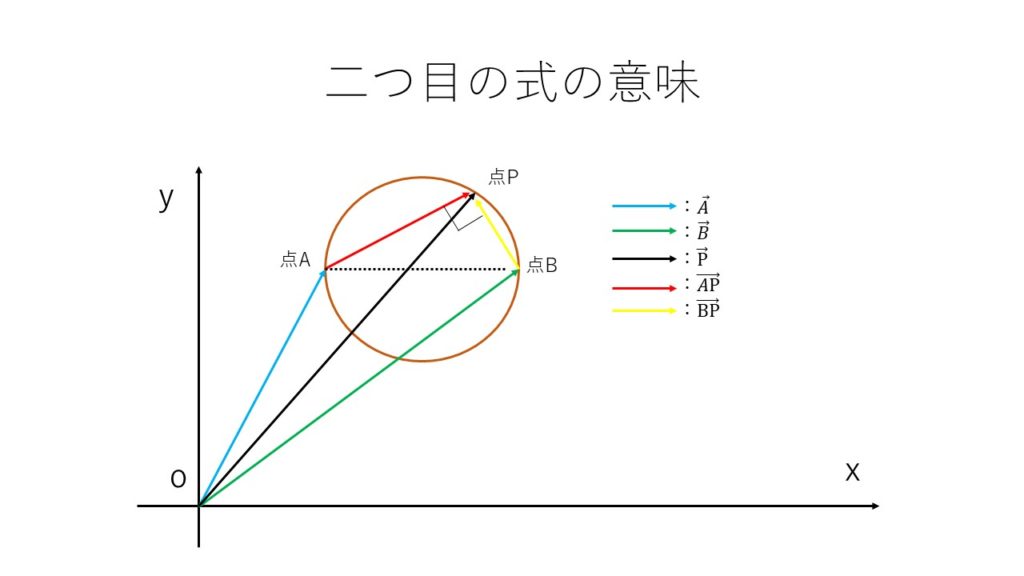
<図3:円周角の定理の利用による円のベクトル方程式2>
※この2つ目の「円のベクトル方程式」の応用として、タレスの定理を使った「球面のベクトル方程式」があります。これは”平面上の円”の代わりに、”空間中に存在する球”をベクトルで表すものです。
この記事を読み終わった後に、ぜひ読んでみてください!
→<参考:「球面のベクトル方程式の求め方がわかる!」>
ベクトル方程式と媒介変数
ここからは、ベクトル方程式の媒介変数(パラメーター)である文字を消去して、普段我々が使っている”直線の方程式”に変形する方法を紹介していきます。
ベクトル方程式の”コツ”
(※):ベクトル方程式で、成分表示を用いた計算をするときには(x,y)のように横に並べる”行ベクトル”よりも\(\vec{d}=\begin{pmatrix}
x \\
y
\end{pmatrix}\)の様に、縦に成分を並べる『列ベクトル』を使ったほうが理解しやすく、計算ミスも少ないです。
ちょっとしたコツですが、行→列にすることによって、すっと頭に入って来やすくなることがあるのでぜひ試してみてください。
成分表示で表されたベクトル方程式
今、図のようなベクトル方程式を次のような成分で表すことが出来るとする。
(成分表示については→「ベクトルの成分表示の説明記事」を参考にしてください。)
$$\vec{d}=\begin{pmatrix}
k \\
l
\end{pmatrix},\vec{p}=\begin{pmatrix}
x \\
y
\end{pmatrix},\vec{a}=\begin{pmatrix}
a_{x} \\
a_{y}
\end{pmatrix}$$
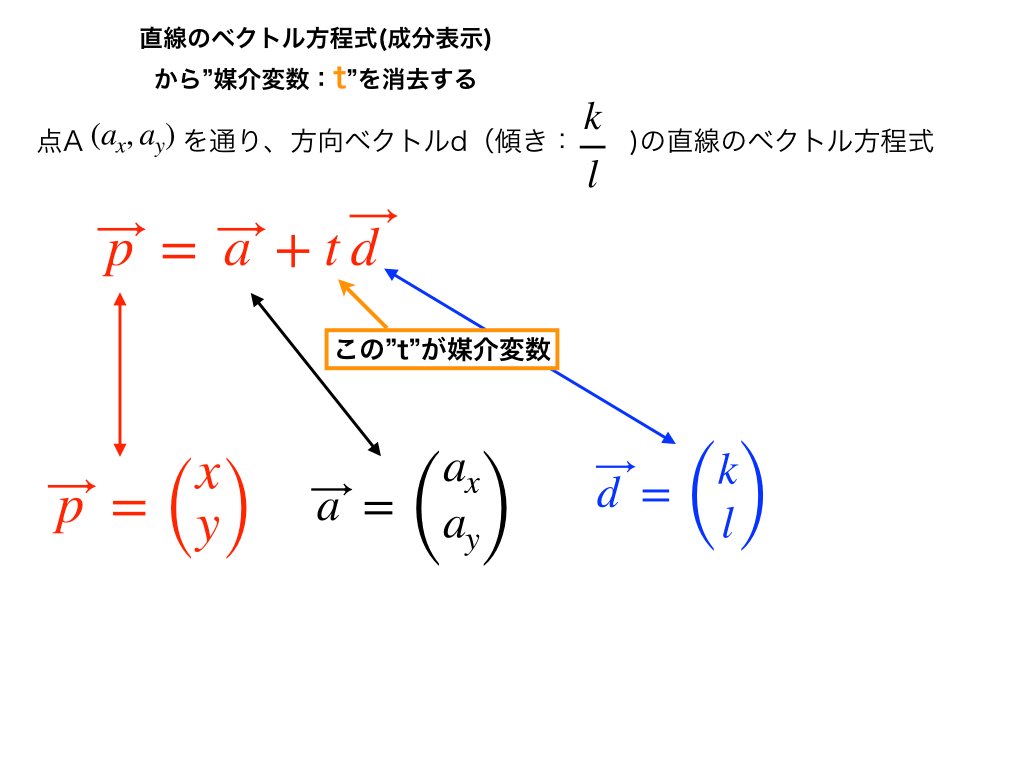
この上図を比較・整理すると次のようになります。

ここで、上図の左下の部分に2つの方程式があらわれます。
媒介変数消去の方法
この\(x=a_{x}+tk\)と\(y=a_{y}+tl\)の方程式から、媒介変数”t”を消したいので、与えられた方程式を変形して\(t=\)の形を作ります。
そして、\(x=a_{x}+tk\)と\(y=a_{y}+tl\)の2本の式のうち、もう一方の式中の”t”に代入し、整理すると”図形と方程式”などで見られる直線の方程式が得られます。
確認例題
では実際に定着用例題を1問解いて、解法bの流れを確認しておきましょう。
$$問:\vec{d}=\begin{pmatrix}
1 \\
3
\end{pmatrix}に平行で、\vec{a}=\begin{pmatrix}
-2 \\
4
\end{pmatrix}$$を通る直線の方程式を求めよ。
確認例題の解答
上の問を図で表すと次のようになります。
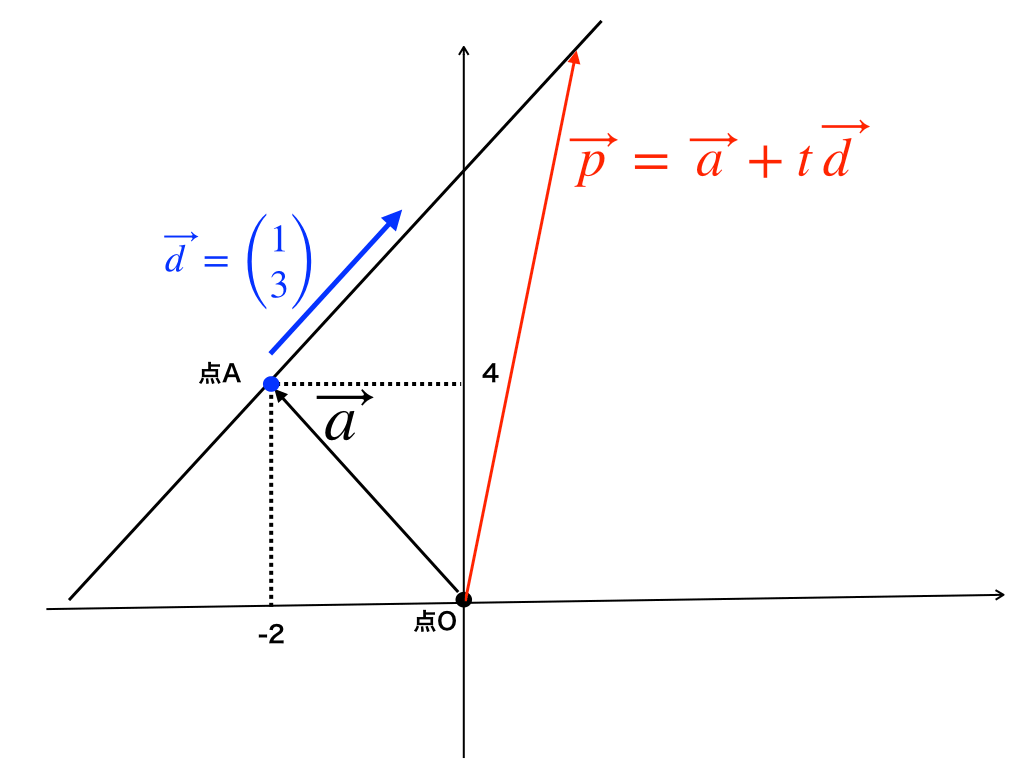
この黒色の直線の方程式を問われているので、先ほどの手順通りx=と、y=の2本の式を作っていきます。
$$\begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
-2 \\
4
\end{pmatrix}+t\cdot \begin{pmatrix}
1 \\
3
\end{pmatrix}$$
よって、$$\begin{bmatrix}
x=-2+t \\
y=4+3t
\end{bmatrix}$$
あとは、媒介変数(パラメーター)であるtを消せば良いので、\(t=x+2\):xの式を移項、\(y=4+3(x+2)\):yの式にtを代入すると、$$y=3x+10\dots (答)$$
が求まりました。
ベクトル方程式のまとめと必見関連記事
このように、これまで図形の問題は数学Aでの「図形の性質」か、数2の「図形と方程式」くらいしかアプローチする手段がありませんでした。
※:追加「図形と方程式での円の表し方」・「複素平面での円の表し方と応用」
しかし、「ベクトル方程式」という強力な道具を手に入れて、
ベクトルで図形を表すことで、新たな手段で図形の問題が解けるようになります。
特に数Aの図形の性質などでは、ある程度「閃き」のようなものが要求されることがありますが、それを回避することができるようになるのです。
続編:空間でのベクトル方程式とベクトル総まとめ
以下の記事では、このベクトル方程式を空間に拡張して「平面のベクトル方程式」について解説しています。
続編>>「【空間ベクトル】直線のベクトル方程式と平面の方程式の求め方【数B】」<<
今回も最後まで読んで頂きありがとうございます!
記事の感想や質問、誤植等が有りましたらコメント欄までお願いします。

