ベクトル「係数の和が1の法則」
ベクトルシリーズ第4弾は、ベクトルの「係数の和が1の法則」の意味と成り立つ理由を解説します。
また、記事の最後には、この『係数の和=1』となることを利用して解く記事を紹介しました。
目次(タップした所へ飛びます)
「係数和1の法則」とは?
例えば平面上に三点O・A・Bがある時、AB上の点をPとすると、OP=s OA+t OBで表す事ができ、
(この時OAとOBは共に零ベクトルではなく、また共に平行ではない、すなわち一次独立な必要があります)一次独立については→「ベクトルの一次独立とは?」
その時の係数の和s+t=1になることを言います。
この条件はベクトルのほとんどの単元を解く際に非常に役に立つのですが、
なぜs+t=1になるのかがあいまいなまま使っている人も多いので、
今回は2通りの方法でその理由を示していきます。

<図1:係数の和が1の証明>
係数和1の証明その一
一つ目は、<図1>にある様に、点Oから点Aを経由して点Pへ進む道のりを考えます。
→ OA+→ ABのt倍した点がPですから、→ABを→ OBー →OAと(後ろー前)に分解して整理すると、
<図1>の様になります。後は、(1-t)=sと置けば、OP=s OA+t OB が言えます。
また、(1-t)+t=1 で(1-t)=sより、s+t=1//
ベクトルの分解や引き算について:「ベクトルの分解をわかりやすく解説!」
係数和1の証明その二
その二は、内分点の公式を利用します。
図と共に解説します。
図1の様に三角形OABがある時、辺ABをm:nに内
分する点をPとします。内分点の公式より、
$$\overrightarrow {OP}=\frac {n\overrightarrow {OA}+m\overrightarrow {OB}}{m+n}$$
となります。これを$$\overrightarrow {OA}と\overrightarrow {OB}$$に分けてみると、
$$\frac {n}{m+n}\overrightarrow {OA}+\frac {m}{m+n}\overrightarrow {OB}=\overrightarrow {OP}$$
と表せました。ここで係数部分に注目して見て下さい!
$$\frac {n}{m+n}+\frac {m}{m+n}=\frac {m+n}{m+n}=1$$
これは=1となりますね!
従って、PがAB上にある時、 $$\overrightarrow {OA}と\overrightarrow {OB}$$の係数和が1となる事が確認出来ました。
外分の場合
外分点を表すベクトルでも『係数の和が1』は成り立ちます。
外分点の公式での証明と、例としてt=2の時の図を載せます。
$$\vec{OP}=\frac{-n\overrightarrow{OA}+m\overrightarrow{OB}}{m-n}$$
$$\vec{OP}=\frac{-n}{m-n}\overrightarrow{OA}+\frac{m}{m-n}\overrightarrow{OB}$$
先ほどの内分の時と同様に、係数に注目すると
$$\frac{-n}{m-n}+\frac{m}{m-n}=\frac{m-n}{m-n}=1$$
となって、確かに外分の場合でも係数の和が1になることが確認できました。
二通りの方法で「係数の和が1の法則」を示す事ができました。
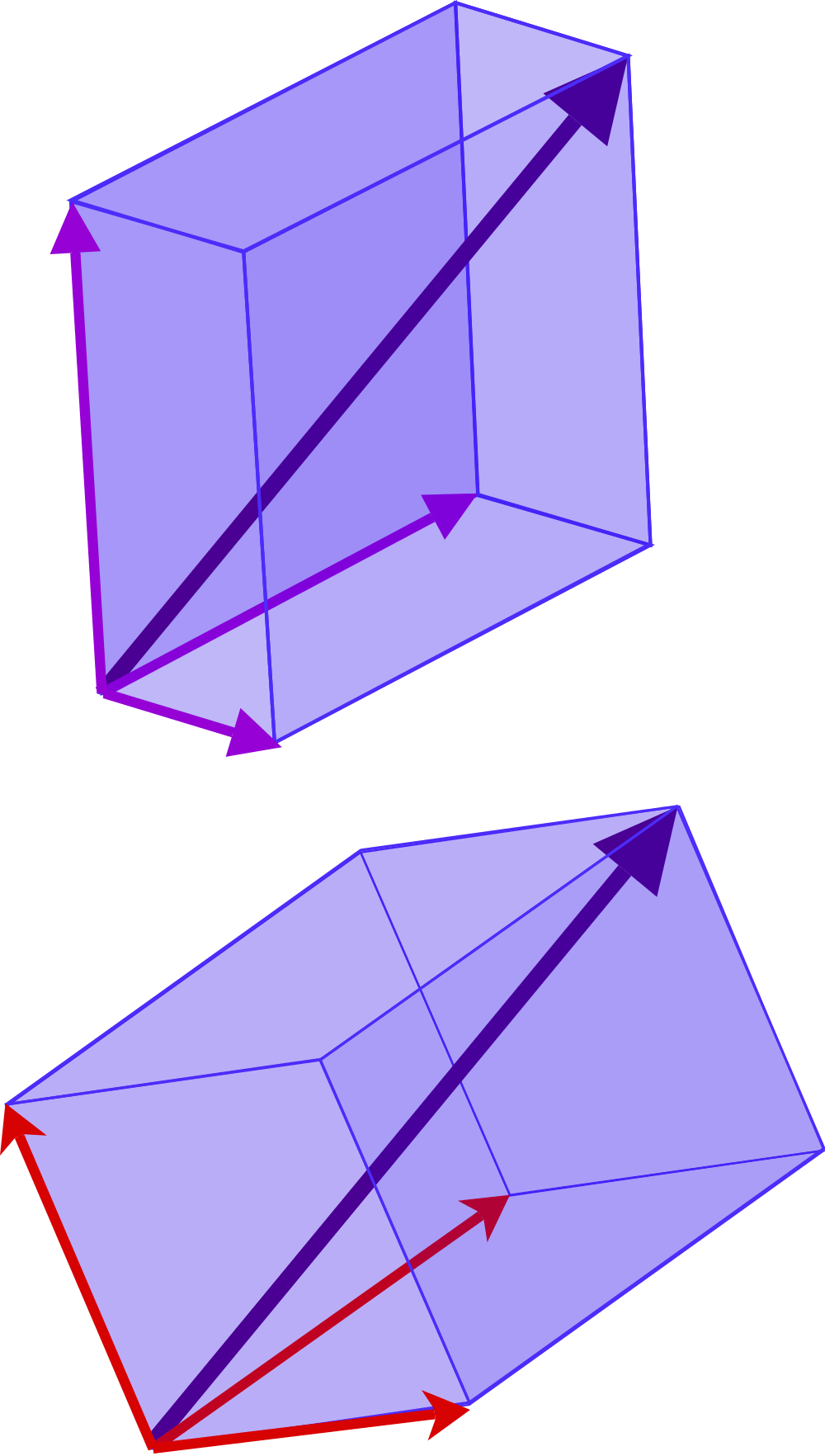
今回は平面ベクトルでの解説でしたが、空間ベクトルの時も同様に係数の和が1の法則を使って問題を解いていきます!
(空間ベクトルの場合には、ベクトル”3つ”の係数の和になりますが、考え方は変わりません。詳しくは以下の記事参照)
係数の和を利用して問題を解く!実践記事
今回の内容を踏まえて、次に読んで頂きたい記事が「ベクトルの終点の存在範囲を得意にする方法」です。
”終点の存在範囲“は差がつきやすい問題ですが、【係数和1の法則】をマスターした後ならば、スムーズに解法が理解できるからです。
右の記事「ベクトルの共面条件/共線条件を利用した頻出問題と解法」では、今回の法則を踏まえた実践的な問題の解き方(空間・平面ベクトル)を紹介しています。
ベクトルの解法:解説記事をまとめました!
続きの「ベクトルとは?ゼロから始める徹底解説記事9選」を読む。
質問・記事について・誤植・その他のお問い合わせはコメント欄までお願い致します!

