軌跡(1):その意味と基本問題の解法
<この記事の内容>:苦手意識を持つ人が非常に多い『軌跡』の基本的な意味や、図示の仕方を学ぶために、2段階の例題を使ってスムーズに理解できるよう解説しました。
2019/08/07(new!):軌跡第二回を作成しました。
目次(タップした所へ飛びます)
軌跡の理解
ここでは、軌跡がどういうものなのか?を理解するための準備問題を紹介し、解いていきます。
導入問題
導入問題1:いまxy座標上に、点A(-3,1)と点B(5,9)がある。
この2つの点と等距離で、なおかつx軸上にある点Pの座標を求めよ。
少し(実際に図をかいて)考えてみてください。
解答解説
さて、以下のような図がかけたでしょうか。
次に行うことは、未知の点Pの座標のうち、わかっていないx座標を適当な文字でおいてあげることです。
(y座標は『x軸上にある』ということから”0”であることが元々わかっています)
ここで、点P(p,0)とおき、問題文の条件より、|AP|=|BP|であることから『三平方の定理』を用います。
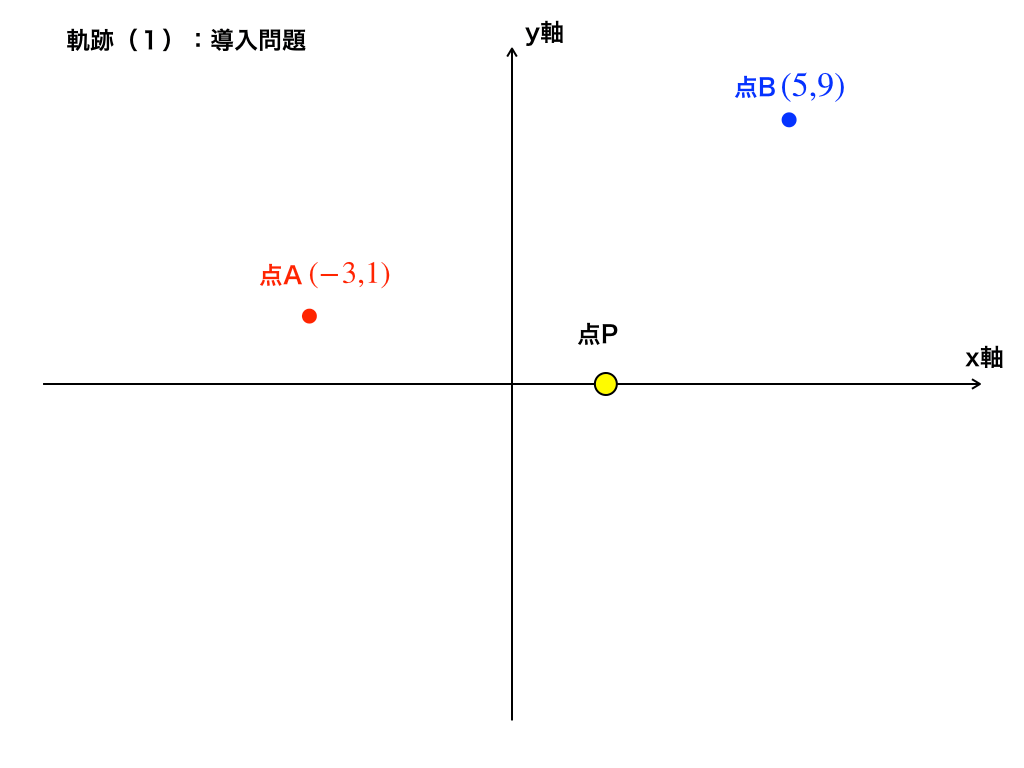
つまり、「赤色の点線の大きさ=青色の点線の大きさ」であればいいので、計算を進めると・・・
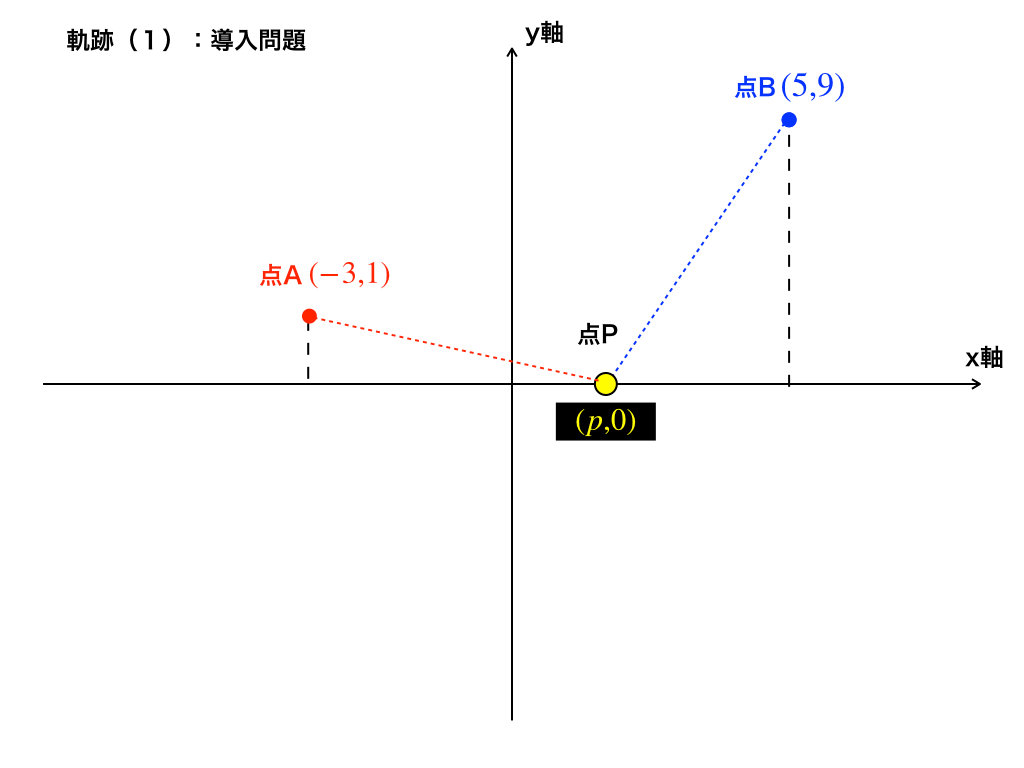
(ここでは、二乗のまま計算を進めます。つまり\(|AP|^{2}=|BP|^{2}\))
$$BP^{2}=(5-p)^{2}+9^{2}$$,$$AP^{2}=(p-(-3))^{2}+1^{2}$$
この2つの値が等しい=等距離なので、展開して整理すると
\(p^{2}+6p+10=81+p^{2}-10p+25\)
\(16p=96\)
\(p=6\)
したがって、点Pの座標は(6,0)・・・(答)
軌跡:”条件を満たす”全ての点の集まり
上の導入問題では、点Pが『x軸上にある』という条件があったため、座標が1つに定まりました。
では、その条件を取り除いた場合、点Pはどのように表すことができるのでしょうか?
実際に問題を解きながら、考えていきましょう。
軌跡:導入問題2
導入問題1と同様に点A、点Bを定めた。
このとき、『それぞれの点から等距離である』という条件を満たす点Pはどのような軌跡を描くか。また、その式を求めよ。
解答・解説と軌跡の図示
さて、この問題2では”y座標の条件”、つまり『x軸上にある』という制限がなくなってしまいました。
では、実際に\(|AP|=|BP|\)を満たす様々な”点P”を座標上に描いてみます。
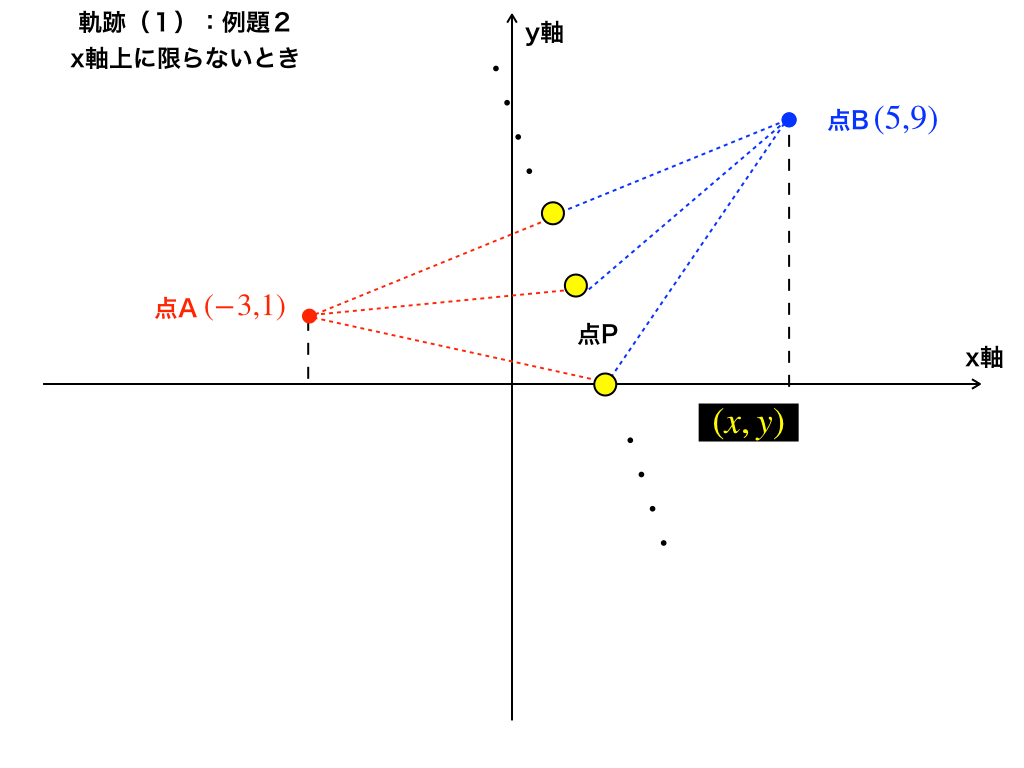
すると、上の黄色の点のように、
・条件を満たす点Pは無数にあること
・その点の集合は『直線』になりそうであること(参考:下図)
が分かります。
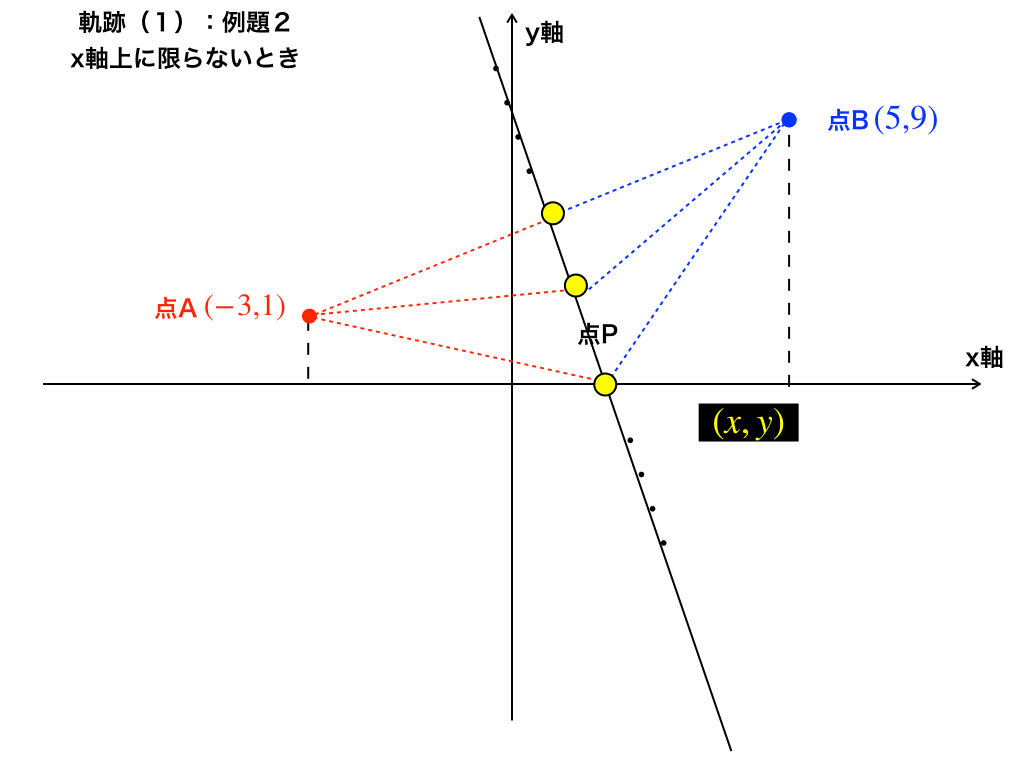
では、ここから実際に点Pの軌跡の方程式の求め方を紹介していきます。
step1:点Pの座標を(x,y)とおく
とりあえず、点Pの具体的な座標はわからないので(x、y)とします。
step2:条件式|AP|=|BP|に代入
次に、|AP|=|BP|より、先ほどと同じように(x、y)座標を使って|AP|,|BP|を計算し=で結びます。
\(\sqrt{(x-(-3))^{2}+(y-1)^{2}}=\sqrt{(5-x)^{2}+(9-y)^{2}}\)
両辺>0より、二乗して
$$(左辺)=x^{2}+6x+9+y^{2}-2y+1$$
$$(右辺)=x^{2}-10x+25+y^{2}-18y+81$$
step3:式を整理する→答
(左辺)=(右辺)より、これを整理すると、
$$6x-2y+10=-10x-18y+106$$
$$よって、y=-x+6\cdots (答)$$
つまり、この点Pの軌跡は『傾きが「−1」でy切片が「6」の直線である』ことが分かりました。
まとめと続編へ
・条件を与えられた時、それを満たす点が無数にあるならば上図のように『線』や『曲線』を描きます。(=軌跡)
・これからも様々な軌跡の問題や、二次曲線・複素数平面などの、【図形と方程式】以外の分野との融合問題を追加していきます。
軌跡との融合分野
以下の記事では、条件が1:1ではないときの軌跡について扱っています。
図形と方程式の関連記事一覧
軌跡の続編
第一回:「今ココです」
>>第二回:「媒介変数(パラメータ)の消去を行う軌跡の問題(入門)」
【領域】についてのシリーズは次のリンクよりご覧下さい。
「軌跡と領域シリーズ(領域1)領域の意味と具体例をイラストで解説!」
「領域2:不等式で表された条件を満たす値(線形計画法)の問題と解法」
今回も最後までご覧いただきまして、ありがとうございました。
「スマホで学ぶサイト、スマナビング!」では、読者の皆さんのご意見・ご感想や、記事リクエストの募集等をコメント欄にて行なっています。
また、お役に立ちましたら、snsでB!やシェアをしていただけると大変励みになります!
・お問い合わせ/ご依頼/その他ご連絡は、【運営元ページ】よりお願いいたします。

