
図形と方程式:直線の式と三角形が成立する条件
<この記事の内容>:数学2『図形と方程式』から、「三角形の成立条件」や「座標上の直線が作る図形の面積の求め方、コツ、公式など」をイラストを交えて解説しました。
目次(タップした所へ飛びます)
三角形の成立条件とは
三角形が成立する・しない条件を求める問題を通して紹介していきます。
不成立条件から考える
三角形の成立条件に関する問題では、『不成立=三角形になり得ない』条件を調べます。
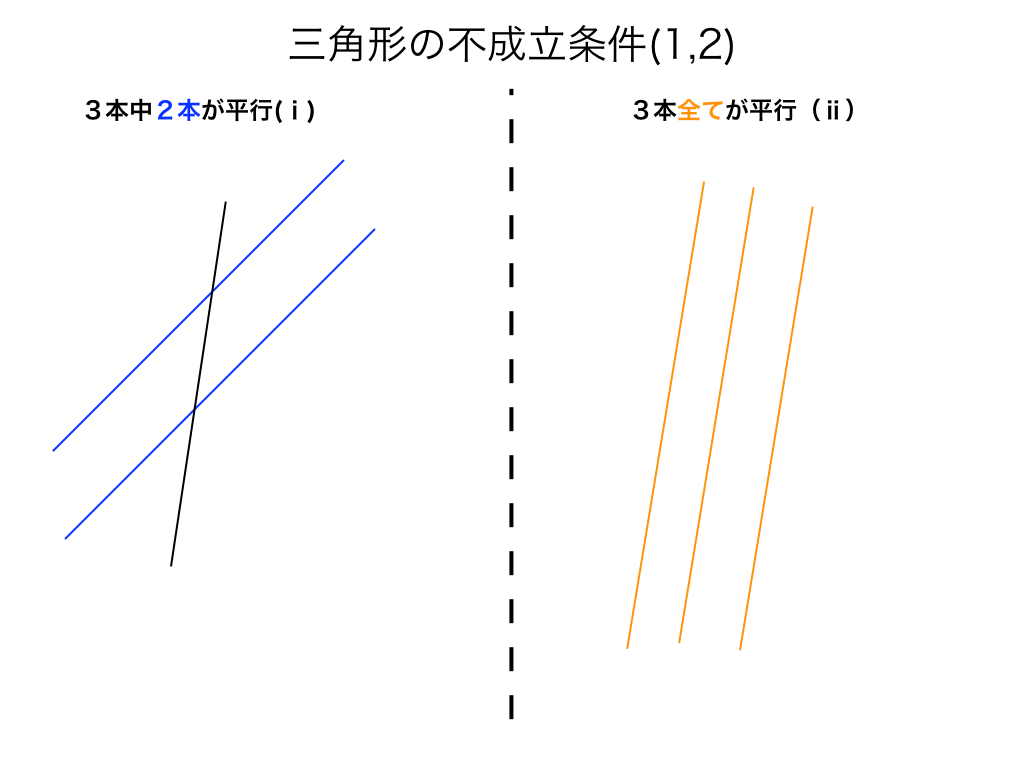
一:2つ以上の直線が並行
まずは、3本の直線のうち2本が平行(図の左)、もしくは3本とも平行である場合(図の右)です。実際にイラストで見てみます。
<2直線or3直線が平行>
当然これではどこまで伸ばしても三角形は成り立ちません。
二:3つの直線が1点で交わる
次は『3直線が1点で交わる時』。これも先にイラストを見てみたほうが早いです。
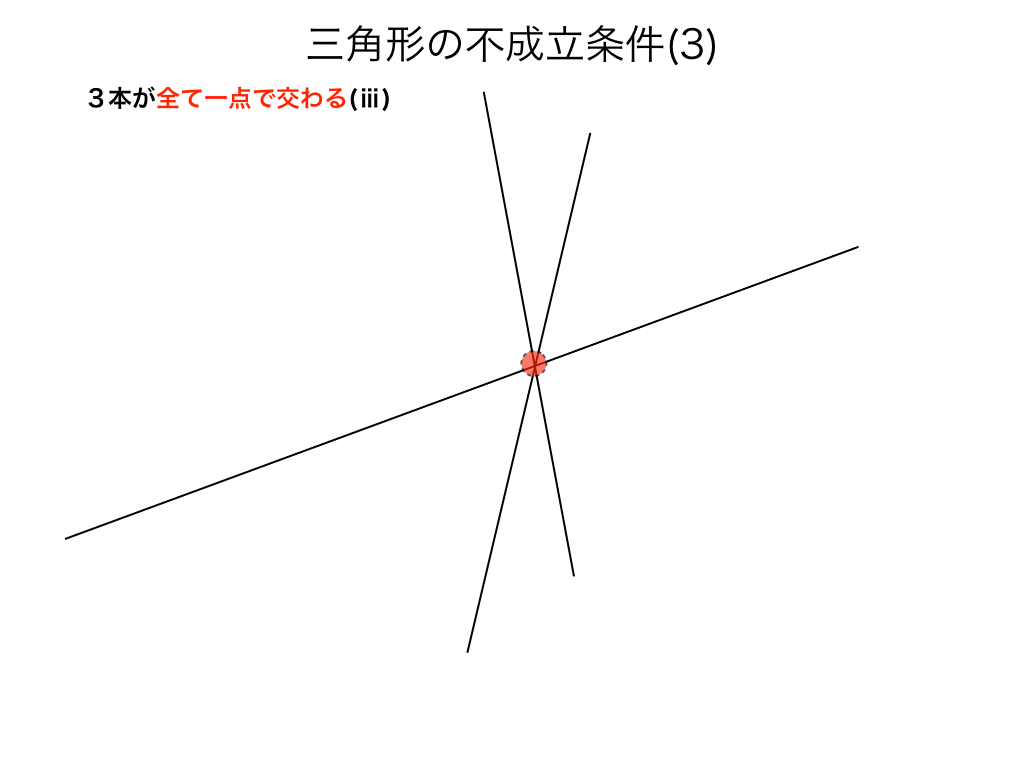
一点で交わる場合も同様に三角形はできません。
では実際にどのような問題が出されるのか、具体的に見てみましょう。
確認問題
いま、x-y座標平面に次の\(y=2x+3,y=-4x-3,y=px+2\)3つの直線がある。(ただし、pは実数)
これらの直線が三角形を作らないpの値を求めよ。
解答
\(y=2x+3\ldots (1),y=-4x-3\ldots (2),y=px+2\ldots (3)\)
いま、どの2直線も平行でないor3直線が一点で交わるとき、三角形ができないから(不成立条件一)、《平行=傾きが等しい》ことを利用します。
(1)と(2)の傾きが異なるのは明らかなので、(1)と(3)、および(2)と(3)の傾きが異なる場合を考えると、、
p=2,-4 のとき不成立条件 1で紹介した平行状態になります。・・・(*)
さらに、(1),(2),(3)が一点で交わる場合も三角形ができないので、(不成立条件二)
まずは(1)と(2)の交点を求め、その点を(3)が通るときのpの値を求めます。
よって、\(2x+3=-4x-3 \leftrightarrow x=-1\)、y=にx=−1を代入して、\(y=1\)
\(-1,1\)を\(y=px+2 が通る時のpは1\)、・・・(**)
(*)と(**)をあわせて、p=1,2,-4 ・・・(答)
三角形の座標上の面積
ここでは、3つの直線の方程式が与えられ、その三直線が作る“三角形の面積を求める方法”を問題を通して解説していきます。
問題
いま、\(y=2x+5、y=x-3、y=-3x+5\)の式で表される三直線が作る三角形の面積を求めよ。
解答解説
まず3直線を厳密でなくて良いのでフリーハンドで描いてみましょう。
\(y=2x+5:①\)、\(y=x-3:②\)、\(y=-3x+5:③\)
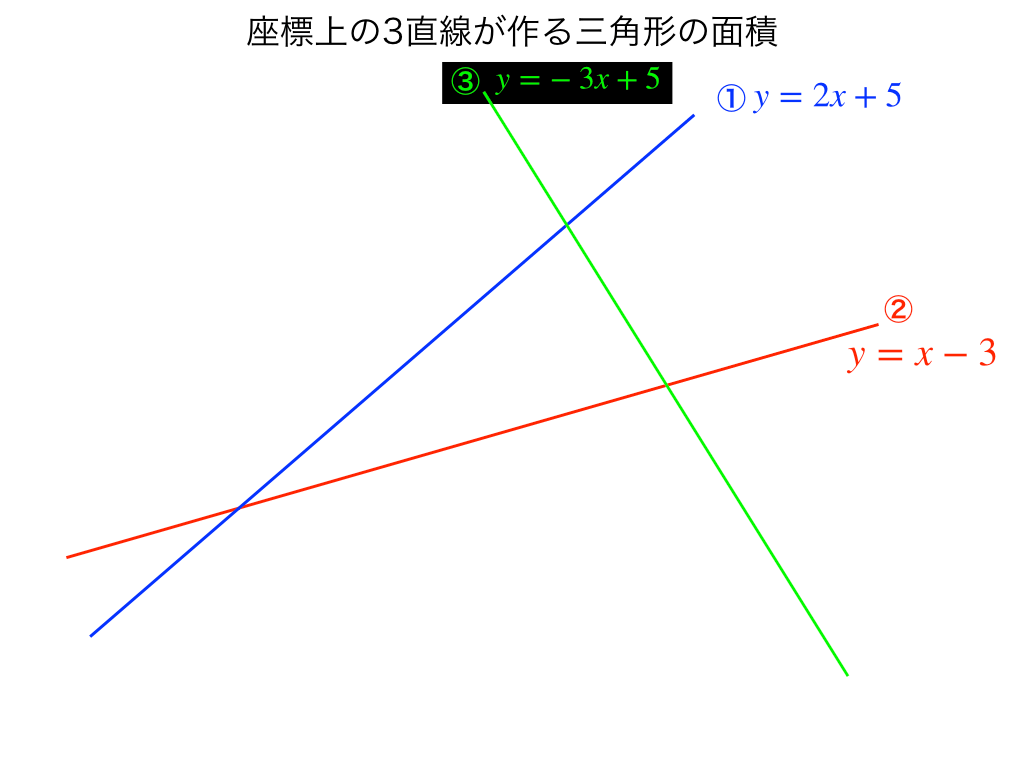
次に、①〜③をそれぞれ連立して以下の項で使う交点を計算します。
底辺の求め方(計算が楽になる選び方)
まず交点を求めて、
直線①と②より、\(2x+5=x-3\leftrightarrow x=-8,y=-11\)
同じく②と③より、\(x-3=-3x+5\leftrightarrow x=2,y=-3\)
最後に①と③より、\(2x+5=-3x+5\leftrightarrow x=0,y=5\)
これで3交点の座標が求まりました。
次に底辺にする部分とその反対側の頂点を選んでいきます。
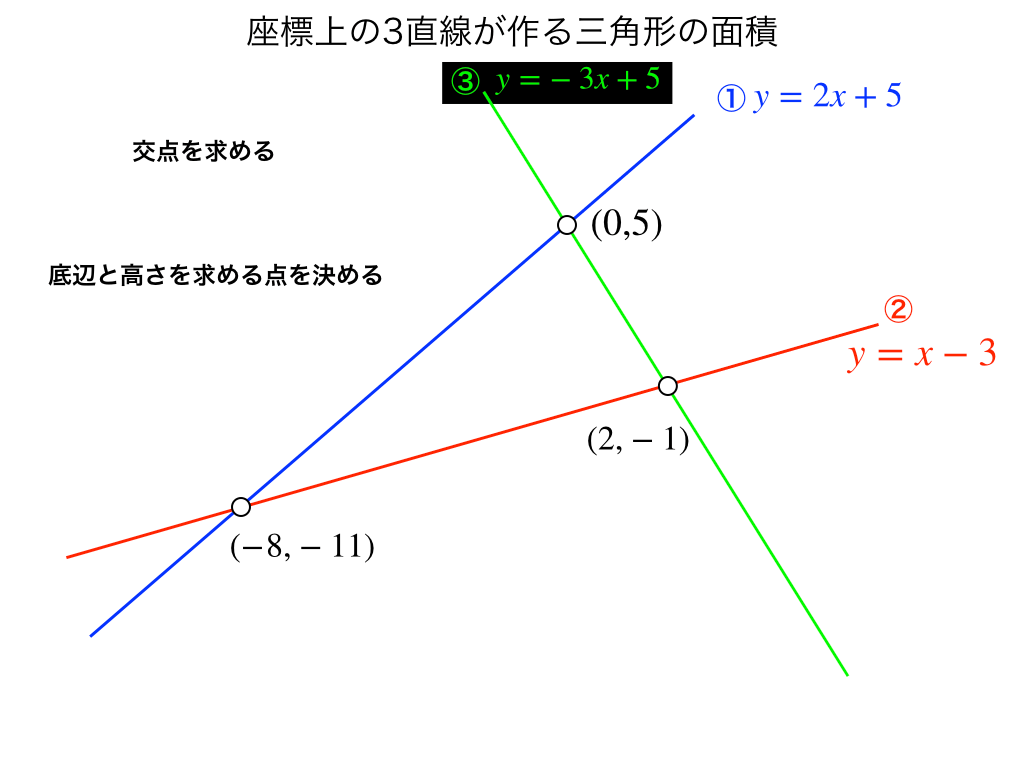
ここで、てきとうに底辺を決めるのではなく、あとあと"計算が楽になるような点・底辺を選んでおく"と時間的な差がつきます。
(楽な点の選び方+)高さの求め方と『点と直線のキョリ公式』
どの交点を選ぶかは、『点と直線の距離』の公式をしっかり理解していれば簡単に見つけることが出来ます。
一応『点と直線の距離公式』を復習しておきます。
直線\(ax+by+c=0\)と\(点(x_{0},y_{0})\)の最短距離dは、
$$d=\frac{|a\cdot x_{0}+b\cdot x_{0}+c|}{\sqrt{a^{2}+b^{2}}}$$
の式で求めることができます。
ここで、公式の分子の計算が楽=ここでは\(x_{0}やy_{0}が”0”\)である点を選ぶことで、余計な計算が不要になります。
したがって、3つの交点のうちから三角形の頂点を\((0,5)\)として、底辺を②の直線中の2交点間の線分とします。
底辺の長さを求め面積計算
最後に、底辺の長さ(大きさ)を三平方の定理or2点間の距離公式で求め、
→先ほどの【距離公式】で求めた“高さ”をかけて
→2で割る
ことで題意の面積が計算できます。
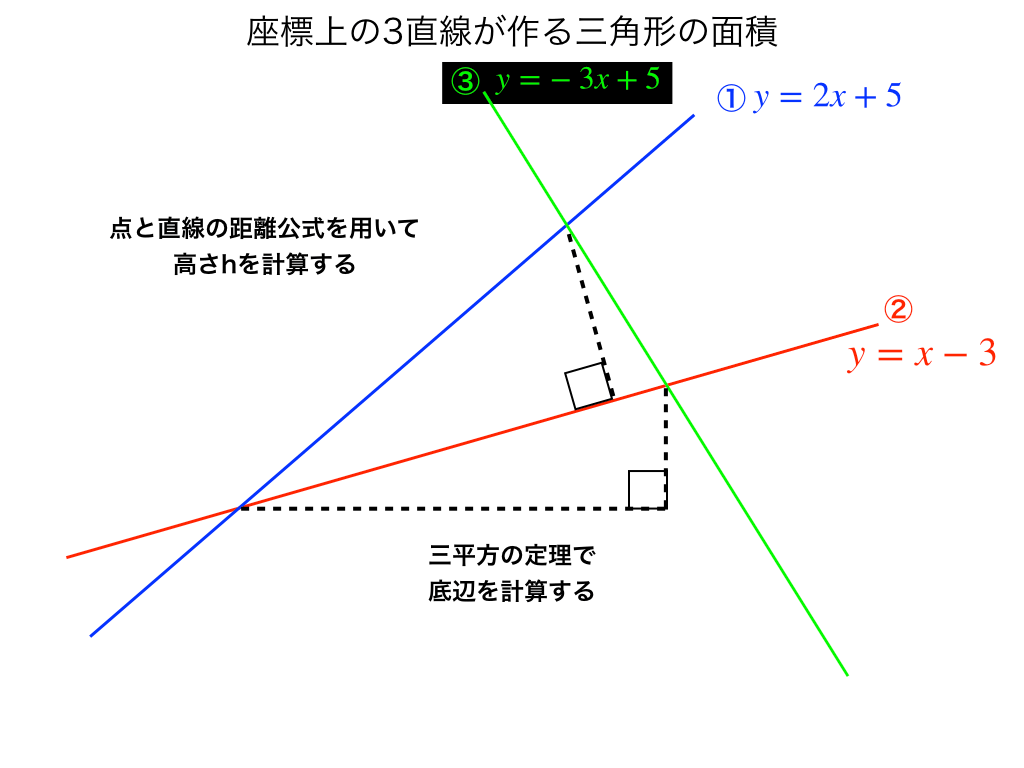
まず、底辺は$$\sqrt{10^{2}+10^{2}}$$、高さが$$\frac{|0\times -1 +5\times 1 -3|}{\sqrt{(-1)^{2}+1^{2}}}$$
したがって$$面積S=10\sqrt{2}\times \frac{2}{\sqrt{2}}\times \frac{1}{2}=10$$
よって面積:S=10・・・(答)
まとめ
・図形と方程式は色々な応用問題が出題される分野で、計算や公式が複雑になる場合も多いです。今後も例題の解説をあげて行くので是非チェックしてみてください。
・その他余裕があれば、『図形と方程式』の標準的な解き方だけでなく、『ベクトル』や『複素数平面』など『別単元の解法を使って解くことができないか?』、を考えるクセをつけると数学の力が飛躍的にアップします。
図形と方程式の関連記事
今回も最後までご覧頂き、有難うございました。
当サイト「スマナビング!」では、読者の皆さんのご意見や、記事のリクエストの募集をコメント欄にて行なっています。
また、 いいね!、B!やシェア、Twitterのフォローをしていただけると励みになります。
・その他のお問い合わせ/ご依頼に関しましては、お問い合わせページからご連絡下さい。

