グラフを描く時増減表を始めから作ってはいけない理由とは?数3微分法

微分と増減表は最後の手段！グラフを描く順序

この記事は、

・グラフを描かせる問題や、求積問題で直ぐに増減表をつくっている人へ

・数学Ⅲの微積を解くスピードと、計算ミスが”大幅に”減る「本質的な」グラフの推測法

を解説したものです。

【NEW！】2019/04/06：関連記事「数学Ⅲを得点源にする為の勉強法」を作成しました。

増減表を描かずにグラフをかく

・2通りのグラフの描き方

・下の方法を勧める理由

・グラフを推測するためにするべき３つの事

・具体例を見てみる

グラフの描き方２パターン

皆さんは、「グラフをかけ」という問題や、「グラフを使って調べる(ex、共有点の個数)」際に何も考えずに微分して、もう一度微分して、増減表をかいて・・・としていませんか？

決して間違いではないですし、教科書通りの「適切」な手順ですが、特に数学Ⅲを得意にしたい場合、筆者は別の手順で進めるべきだと考えています。

(普通) 関数→微分(細部を調べる)→グラフ全体

＜この”普通の方法”は当然完璧にしておかなければいけません。不安のある人は→「三次関数のグラフの描き方」←で”増減表”を使った方法を再確認しておきましょう。＞

(推奨)関数→グラフ全体を思い浮かべる→微分

なぜ、この方法を勧めるか。

理由は幾つかあります。

数学Ⅲで扱う関数は特に複雑なものが多いので、計算ミスをしやすく、また時間も掛かります。

・グラフ全体のおおまかなイメージをせずに微分を始めてしまうと、ミスに気付かない恐れが非常に高いです。

・また、到達するグラフの見通しが立っていないので、効率的に必要な計算だけする＝計算にかける時間を削る事が出来ない事も理由の一つです。

・そして最大の理由は、この方法に慣れる事で数学が「見えて」くる、という無視出来ない効果があるからです。

グラフをイメージする方法

利点が多いこの方法ですが、言うは易く行うは難しな面もあります。そこで最短で身に付ける為にするべき事を紹介します。

(１)最低限の基本的なグラフの形は覚えておく

指数関数や対数関数、基本的な分数・無理関数などのグラフは前もって頭に入れておきます。

$$y=e^{x},y=\log x,y=\frac {1}{x}$$

$$y=\frac {1}{\sqrt {x}},y=\sqrt {x}$$

等々一通りの有名なグラフの形は覚えておきましょう。

(２)グラフの符号が変化するxの値や、分母が0になるxの値を抑える。

y＝(xー2)(x+3)ならば、x=2、-3を境に符合が変わるのでx=2、-3をチェック

y＝1/x ならば、x=0を取れないのでx＝0の左右極限を調べる。等。

(３)limx→±∞や、片側極限などの計算に慣れる

上述した様に、左右極限やxを±∞へ飛ばした時の計算を早くする為に、極限計算の練習をする。

＜参考：「極限を得意にするための解説記事まとめ」＞

では実際にどの様に進めるかを見ていきます。

例題の関数は筆者が執筆中に思いついた(てきとうな)ものです。

実際の手順

＜例題＞次の関数のグラフをかけ

y＝(xー2)(x+3)/e^x

$$y=\frac {( x+3) ( x-2) }{e^{x}}$$

先ず、$$分数を外す為にy=( x-2) ( x+3) e^{-x}に変形し$$、

$$y=( x-2) ( x+3) ,y=e^{-x}$$のグラフをメモ程度に書きます。

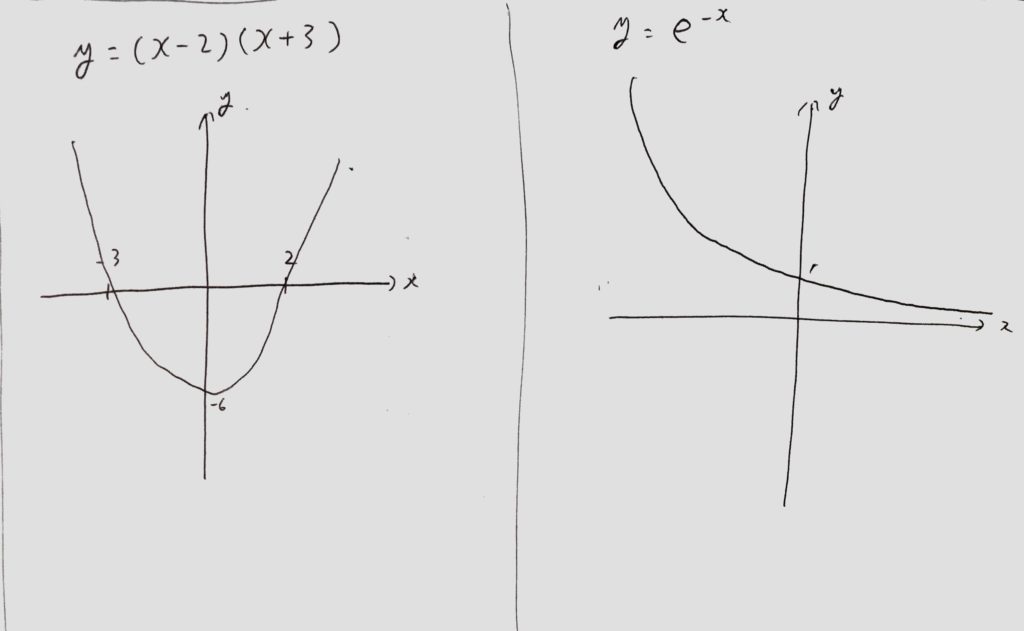
＜図１：問題の関数を構成する有名関数のグラフ（パッと頭に浮かぶようにする）＞

次に、メモの＜図１＞より$$y=e^{-x}は常に正$$

y＝(xー2)(x+3)は下に凸のグラフで符合はx=2、-3で変化する(∴x=2、-3の時y＝0)事をチェックします。

$$するとy=( x-2) ( x+3) e^{-x}$$

のグラフがいるゾーンが大方推定できます。

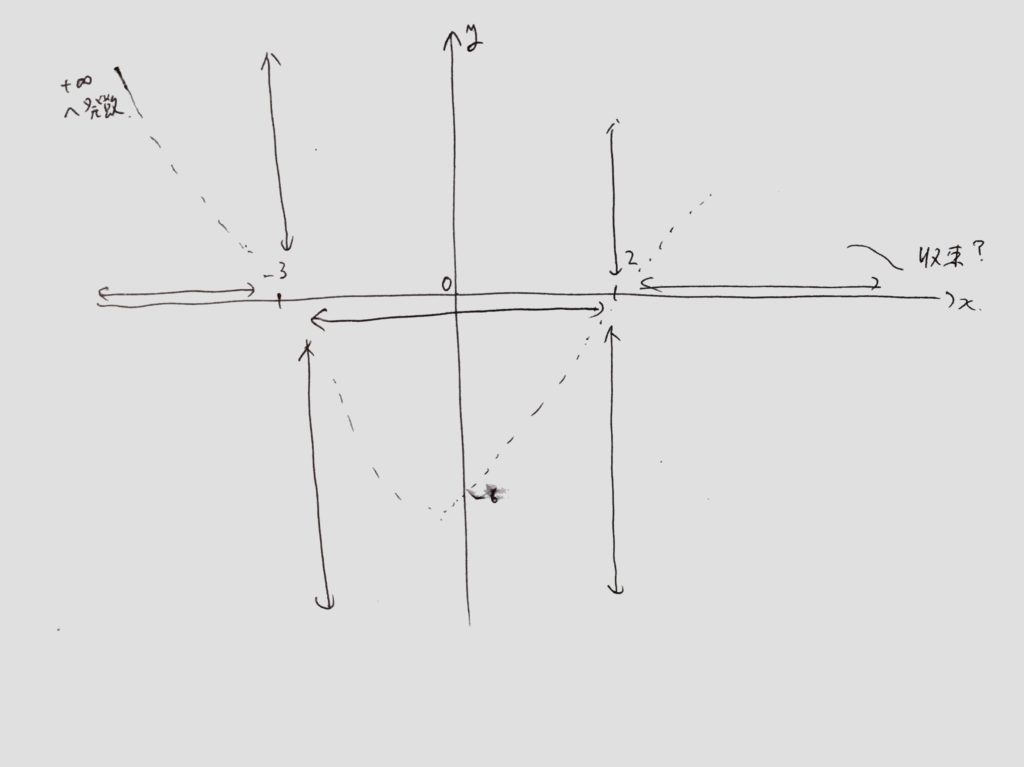
＜図２：予測したグラフの形＞

後は、xを±∞へ飛ばした時の挙動をチェックし、大体のグラフの概形を描きます。

$$\lim _{x\rightarrow +\infty }( x-2)( x+3) e^{-x}=0$$

$$\lim _{x\rightarrow -\infty }( x-2)( x+3) e^{-x}=+\infty $$

ここ迄でほぼグラフは出来てしまうのですが、変曲点や極大極小を問われる場合は、ここでやっと微分をします。

(逆に厳密な事が問われず、体積や面積を求めるだけなら、このまま積分に進みましょう)

先ほども言いましたが、既に概形が分かっているので、ミスの可能性と計算チェックの時間を大幅に削れます！

$$\begin{aligned}y=( x-2) ( x+3) e^{-x}\\
=( x^{2}+x-6) e^{-x}\end{aligned}$$

$$\begin{aligned}y'=( 2x+1) e^{-x}-( x^{2}+x-6) e^{-x}\\
=-e^{-x}( x^{2}-x-7) \end{aligned}$$

数字が汚くなってしまいましたが、$$x=\frac {1\pm \sqrt {29}}{2}$$で極大極小をとるようです。

今回はグラフを書くのが目的なので、＜図１＞〜＜図２＞より、

例題のグラフは下の様になります。

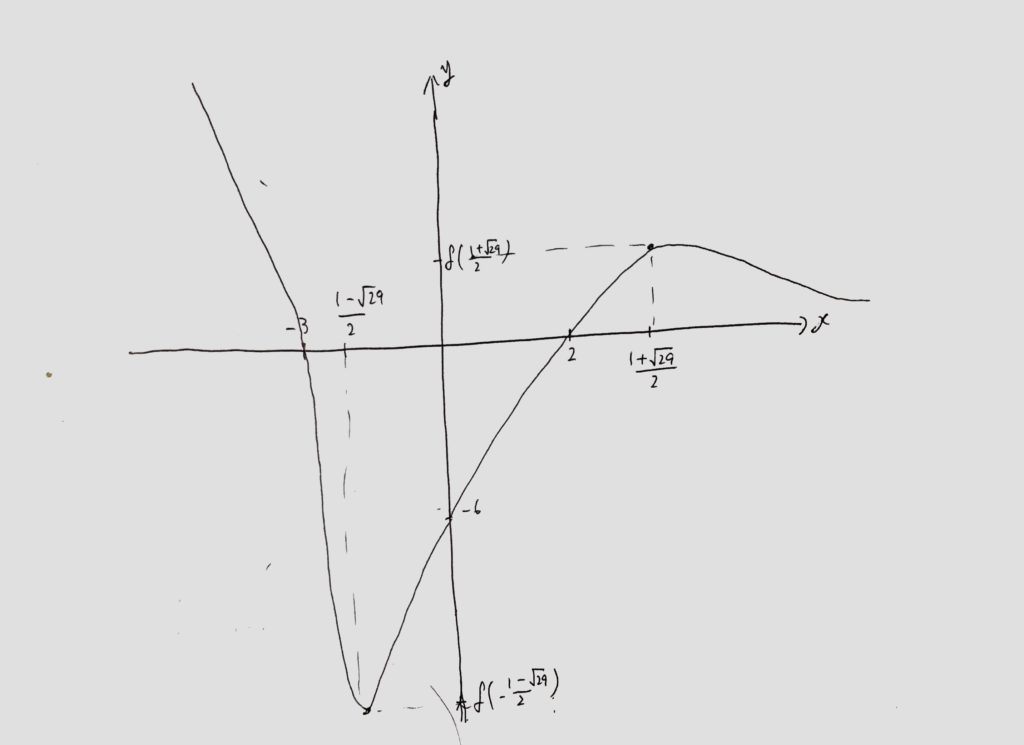
＜極値まで調べたグラフの概形＞

まとめと数学3：微積分の関連記事へ

この方法は慣れるのに少し時間が掛かりますが、一度習得すると式を見ただけで大体の関数のグラフがイメージできる様になります。

計算のスピードと正確さが命運を分ける数３においては、特に重要なスキルなので、是非色々なグラフを自分で試行錯誤しながら作って見て下さい。

＞＞NEW！：「数学３を得点源にして合格する為の勉強法【予習・復習編】」

その「積み重ね」がやがて大きな差になります。

＜数学Ⅲの微分・積分の重要公式・解法総まとめ＞へ戻る

今回もお疲れ様でした。

お役に立ちましたら、シェア・Twitterのフォローをお願いします。

質問、リクエスト、その他お問い合せはコメント欄までお願い致します。

関連記事→「極限を得意にする記事6選まとめ」を読む。