
判別式:Dとは?【入門~基礎レベル】
<この記事の内容と対象>:「判別式D」がイマイチ良く分からない、「d/4」はいつ使うの?と言った人に向けて、0から意味/使い道を紹介しています。
目次(タップした所へ飛びます)
判別式D【仕組みと公式理解編】
仮に、2次方程式:\(ax^{2}+bx+c=0\)(ただし、a,b,cは実数でa≠0)があるときに、\(D=b^{2}-4ac\)というものを”判別式”として紹介され、方程式の解の個数などを調べるときに使っているかと思います。(下で詳しく紹介します)
が、Dはそれだけにとどまらず、「"整数"や"高次方程式"、"いろいろな関数の方程式"」など様々な分野と融合する、”数学においてなくてはならない道具”と言えます。(ex:「二次関数の解の配置問題(応用レベル)」など)
理解があいまいな人は、必ずこの記事で理解しておいてください!
Dの式はどこから来るのか?
さて、\(D=b^{2}-4ac\) はどこから来て、なぜ解の個数を”判別”できるかについて即答できるでしょうか?その答えを「2次方程式の”解の公式”」を振り返りながら見ていきます。
”解の公式”の振り返り
\(ax^{2}+bx+c=0\)の解(x=●)を求める際、因数分解(参考:「因数分解のやり方と公式まとめ」)ができないときに『解の公式』を使います。
$$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$$
”D”の値で”解の個数”がわかる理由
ここで分子のルートの中身に注目すると、判別式:Dと同じ式になっている事がわかります。
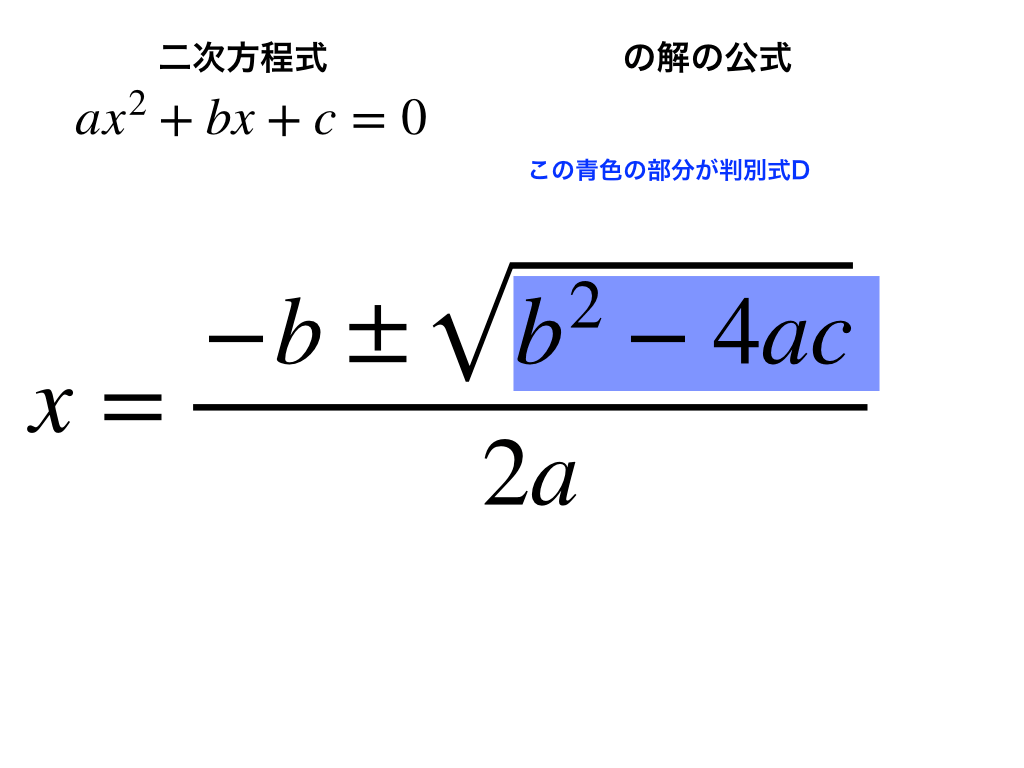
そこで、次のように書き換える事ができ、
$$x=\frac{-b\pm \sqrt{D}}{2a}$$
分子の”プラスマイナス”の部分と、Dの値に注目すると・・
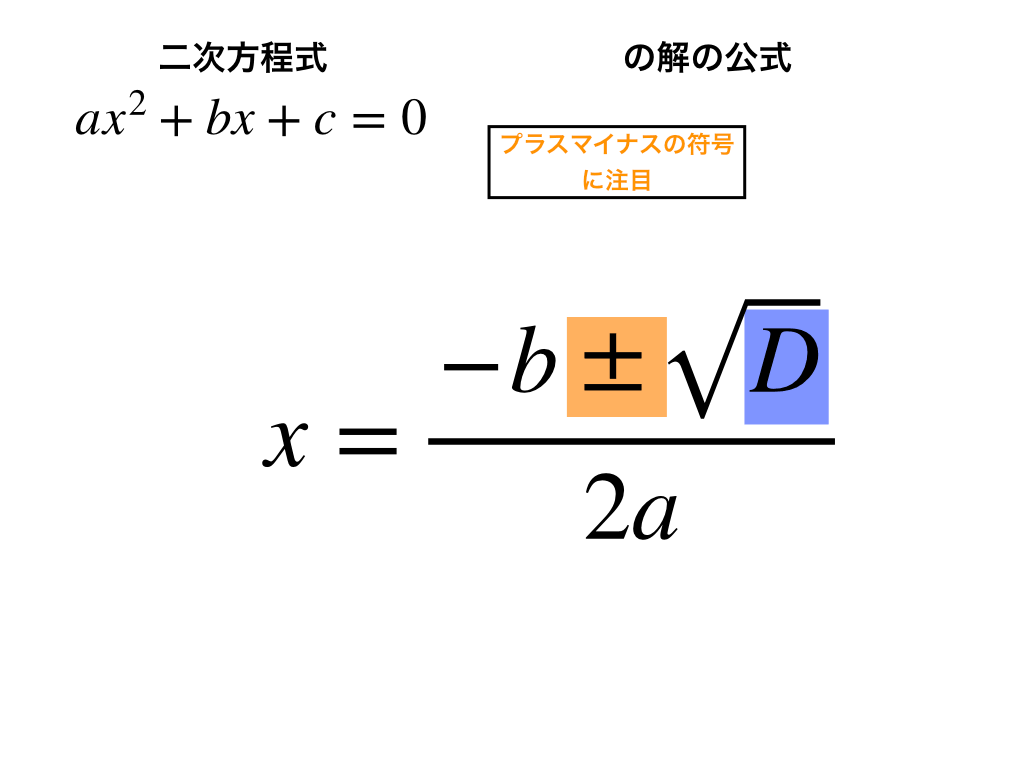
以下の図のように3パターンに”場合分け”する事が可能です。
つまり、
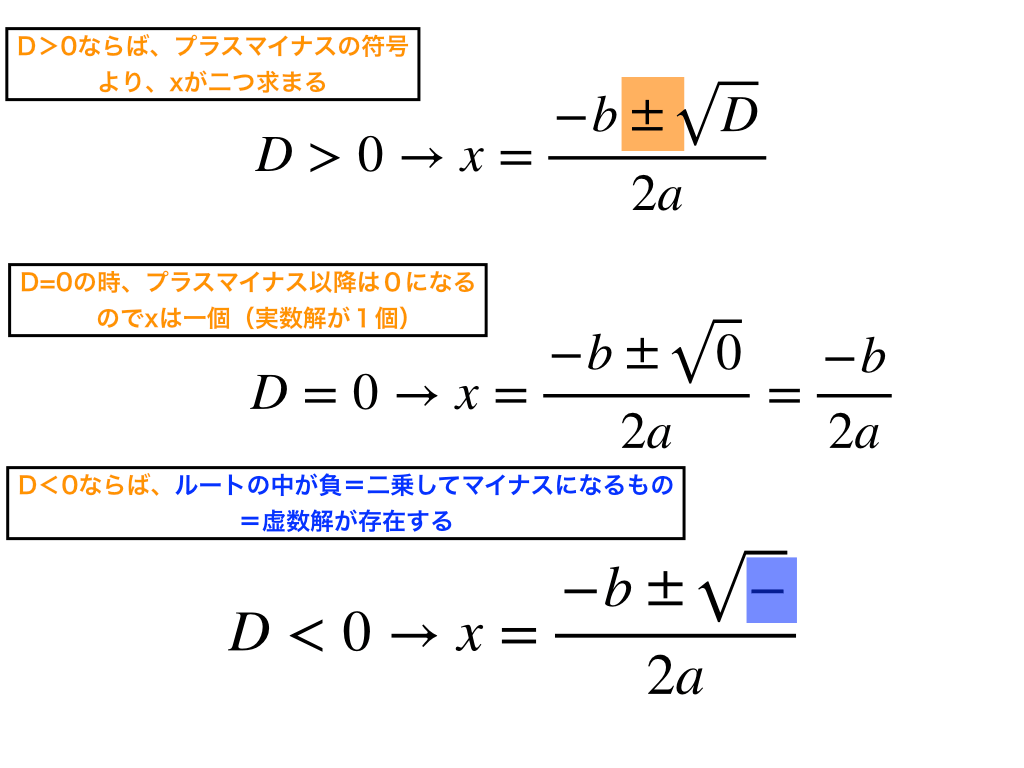
・D=0なら分子のプラスマイナスは関係なくなり、『xは1個』に決まります。
・D>0ならば、\(\sqrt{D}\)も当然0より大きいので、$$x=\frac{-b+\sqrt{D}}{2a},\frac{-b-\sqrt{D}}{2a}$$の2解を持つ事がわかり、『xの実数解は2個』、
・D<0のとき、\(\sqrt{負の値}\)⇔2乗して負になる値=虚数解のみを持つ=”実数の範囲”では”解を持たない”。したがって、『実数解は0個』と判別できます。
これが、Dを計算することによって(実数)解の個数がわかる理由(仕組み)なのです。
『D/4』の意味と使う時/使って良い訳
教科書や参考書・問題集などでは、判別式の計算を早くするために、いわゆる『\(\frac{D}{4}\)』が広く使われています。
その仕組みをここで紹介しますが、もし”ややこしい”と思ったら無理に使う必要はありません。
十分に慣れてから使う方が、曖昧なまま計算ミスをするよりはるかに良いからです。
・\(\frac{D}{4}\)を使う目安:\(ax^{2}+bx+c=0\)の【"b"が偶数】である時。
(理由:偶数を2乗すると必ず『4の倍数』になることと、(ー4ac)の部分は必ず4で割り切れるので、\(\frac{D}{4}=\frac{b^{2}-4ac}{4}\)のように、あらかじめ”4”で割っておくと計算が楽になります。)
・また、【D/4】とDの符号は必ず一致する(もっと言えば、『0か、0未満、or、0より大きい』のいずれかであるか、が分かれば良いので正確なDの値は必要ない)事が、\(\frac{D}{4}\)を使う理由です。
判別式の使い方:問題編(+α)
ここまで、Dを使う理由や仕組みについて紹介してきました。
ここからの「問題編」では具体的な問題を使って、”判別式の使い方”を身につけていきます。
練習問題
以下の問(一)〜(三)の2次方程式がいくつの実数解を持つのかを答えよ。
(一):\(2x^{2}+3x-1=0\)
(二):\(x^{2}+12x+9=0\)
(三):\(3x^{2}-2x+2=0\)
解説
いずれも単純に計算を進めるだけの確認問題です。
(解一):\(D=3^{2}-(4\cdot 2\cdot -1 \)=9+8=17>0 より、2個・・・(答)
(解二):問二は折角なので\(\frac{D}{4}=(\frac{b}{2})^{2}-ac\)を使って解いてみましょう。
\(\frac{D}{4}=(12/2)^{2}-9=36-9=27>0\)より、2個・・・(答)
(解三):\((-2)^{2}-(2\cdot 3)=-2<0 \)より0個・・・(答)
応用問題+α:虚数解について
次は、少し応用させた問題です。
係数決定・範囲の問題
この二問は解の個数を聞いているのではなく、その逆に実数解の条件から→二次関数の係数の値・範囲を問うものです。
(四):\(mx^{2}+3x-1=0 (m≠0)\)が重解を持つとき、mの値を求めよ。
(五):\(2x^{2}+nx+3n=0 \)が虚数解のみを持つ(=実数解の個数が0)の時のnがとる値の範囲を答えよ。
<解答・解説>
(解四):重解を持つ=解が"一つ"="D=0"なので、mの値は
\(D=9+4m=0\leftrightarrow m=\frac{-9}{4}\)・・・(答)
(解五):次は"nの範囲"を問われていますが、やることは変わりません。
\(D=n^{2}-4(3n)(2)<0 より、\)
\(n^{2}-24n<0 ⇔n(n-24)<0\)
したがって、\(0<n<24・・・(答)\)
判別式の公式Dのまとめ
初めにも書きましたが、判別式は整数問題→「整数問題(実数条件からの絞り込み)」など、様々な分野に顔を出して来ます。
よく復習をして、キッチリ理解しておきましょう!
関連記事へ(方程式・解の配置・存在範囲など)
いろいろな種類の方程式・不等式について
>>「高校数学で学ぶ”方程式”・”不等式”の総まとめページ」
「スマナビング!」では、読者の皆さんのご意見・ご感想を【コメント欄】にて募集中です。(※):現在個々の問題のご質問に関しては、時期的に対応できない場合がございます。
(その他の誤植の指摘等は引き続き募集しています。)
・お問い合わせ/ご依頼/その他のご連絡は【運営元ページ】よりお願いいたします。

