化学平衡(2):平衡定数の求め方
<この記事の内容>:二酸化硫黄\(SO_{2}\)と三酸化硫黄\(SO_{3}\)の生成反応を通して、化学平衡の意味や"平衡定数K"の求め方、計算問題の解き方
(+そのために必要な表の描き方)、反応速度との関係などについて解説しています。
<関係する記事については、この記事の最後にまとめています>
目次(タップした所へ飛びます)
化学平衡とは?
シンプルに言うと、(『化学反応の正反応(反応物→生成物)』の速度)と=(『逆反応(生成物→反応物)』の速度)が同じになって、(あくまで"見かけ上")反応が停止したような状態です。
この意味を少しずつ解き明かしていきます。
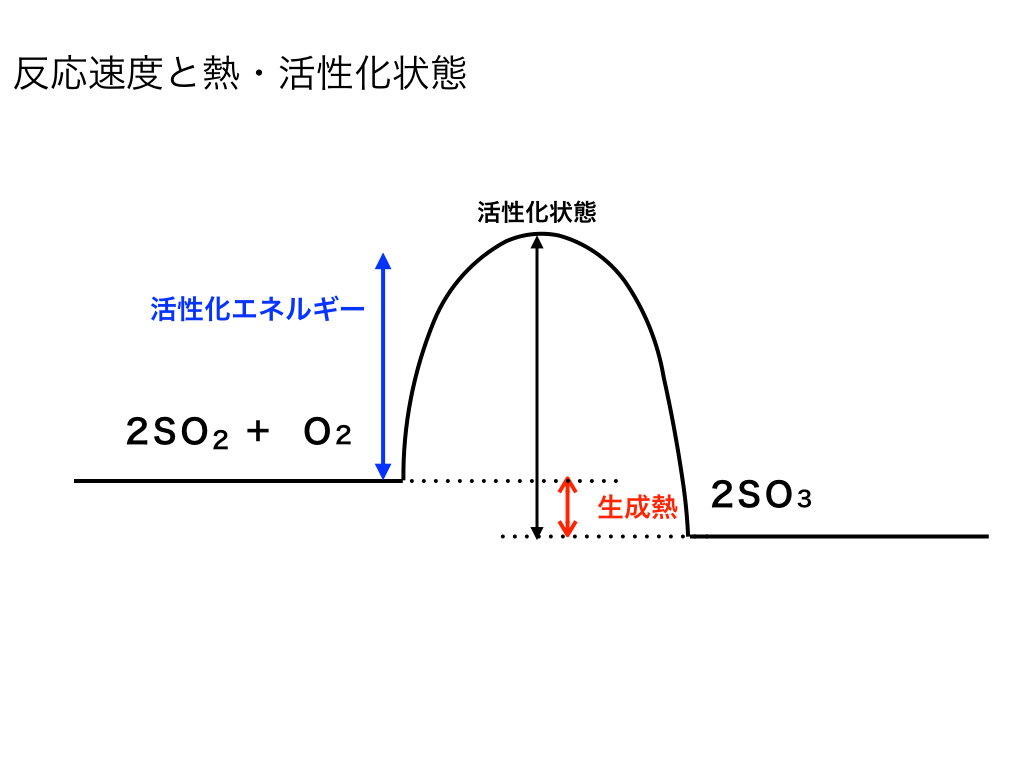
平衡状態と反応速度の関係
平衡は『正方向の反応速度』=『逆反応の反応速度』
となった場合に起こります。(詳しくは→「反応速度(定数)の意味と求め方」をご覧ください。)
平衡の移動と関連する『原理』
ここまで紹介してきた『平衡』ですが、様々な要因によって、”生成物側”or”反応物側”にかたよる事があります。
(ex;温度や圧力を上げ下げする、希ガスを注入する、等々・・・)
このようなときに、『どちら側にかたよるか』を判断する手がかりとなるのが「ルシャトリエの原理」と呼ばれるものです。
(詳細は→『”ルシャトリエの原理”8種類をまとめて解説!〜希ガスに要注意〜』をご覧ください)
化学平衡の仕組みと解法を頻出問題で学ぶ
さて、ここまでは若干抽象的な話が多かったので、難しく感じた方も多かったかもしれません。
ここからは、硫黄酸化物に関する具体的な問題を使って、『どのような出題をされて、どう解いていくのか』を解説します。
硫黄酸化物の問題
<問題>:いま、体積がV(L)の容器の中で、\(2SO_{2}+O_{2}\leftrightarrow 2SO_{3}\)の(可逆)反応が起きている。しばらくすると、この反応は平衡状態になった。
はじめの二酸化硫黄SO2の量をX、酸素O2の量をYとし、三酸化硫黄SO3は存在しなかったとして、以下の問いに答えよ。
ただし、回答には問題文中に与えられた文字を使用して良いものとする。
(1):酸素がαだけ減少して平衡状態となった。このときの「SO2、SO3、O2 」それぞれの物質量を求めよ。
(2):平衡定数をKとするとき、その値を与えられている文字で表し、単位とともに答えよ。
(3):X=4Y、\(α=\frac{Y}{3}\)としたときのKを求めよ。
平衡定数を求める準備:「図(表)をかく」
このような平衡に関係する問題では、必ず
・『反応前』
↓
・『反応中』
↓
・『平衡状態』
の場合における、それぞれの量の変化を図に書いて解いていきます。
(※参考:以下の表)「"過不足"が生じる化学反応の問題」の記事でもほぼ同じ表を使います。)
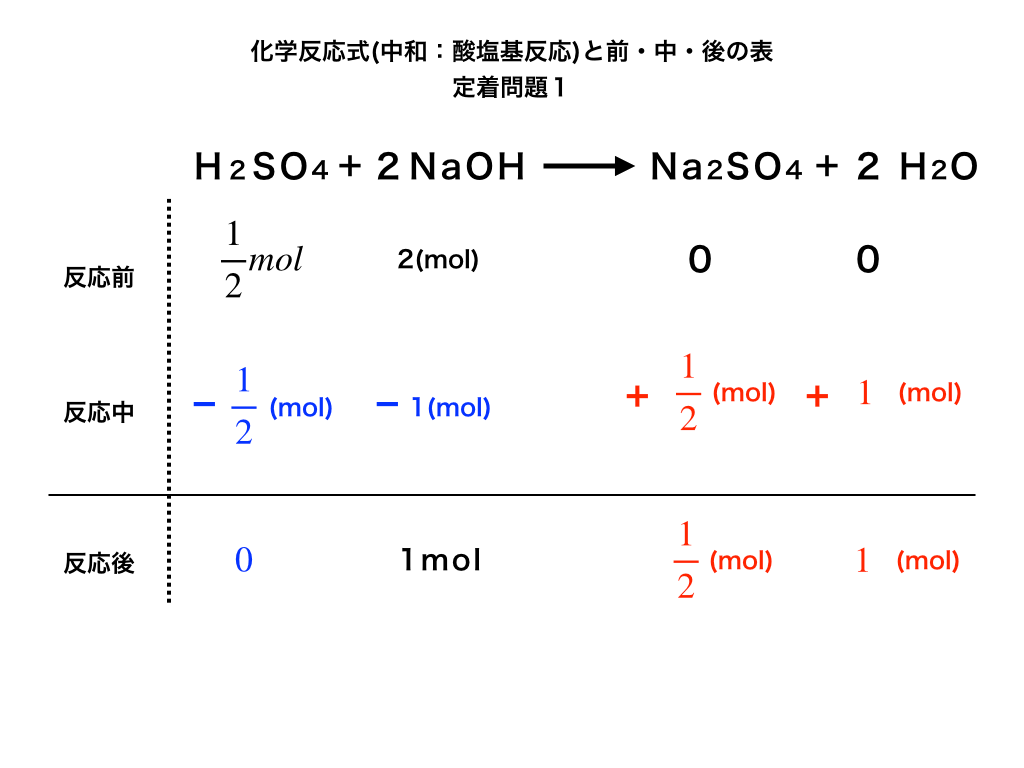
(イメージ:過不足の表)
この表を平衡の問題では、次のように変化させます。
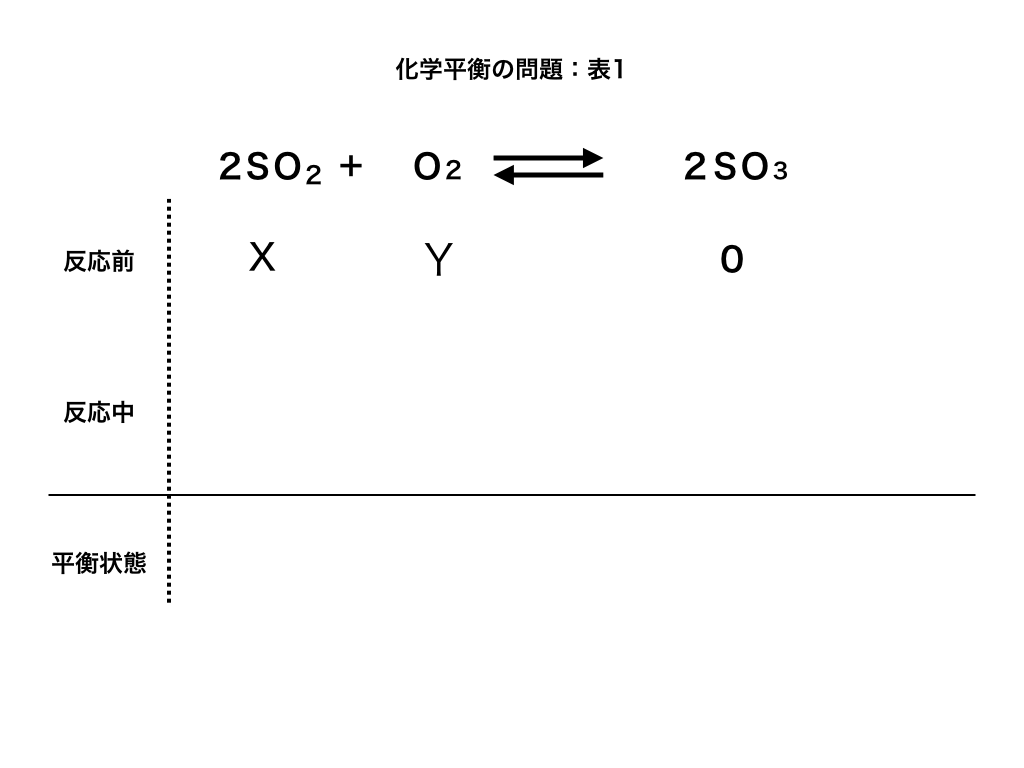
<硫黄酸化物の問題の(1)>
平衡定数の公式
平衡定数はKであらわし、求めたい反応が次のような式で表される場合、
$$\alpha A+\beta B\leftrightarrow \gamma C+\delta D のとき、$$
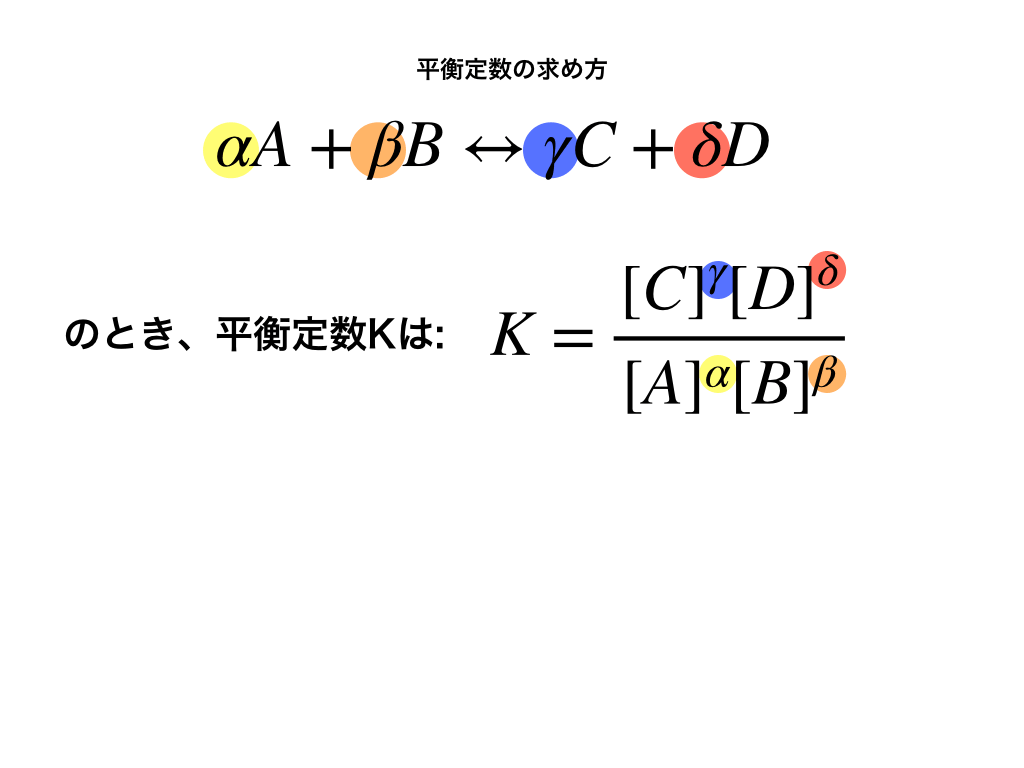
上のイメージ図のように、分母・分子に\([A]=\frac{Aの物質量(mol)}{V(L)}\)、\(同様に[B],分子に[C],[D]\)を計算して、反応式の各係数の値だけ●乗します。
$$平衡定数K=\frac{[C]^{\gamma}[D]^{\delta}}{[A]^{\alpha}[B]^{\beta}}$$
問題の解説
では、先ほどの問題(1)〜(3)を解いていきましょう。
解説(1):前・中・平衡の表を書く
問題を振り返っておくと、反応が始まる前は、SO2がX、O2がY、SO3が0であり、平衡状態になるまでにO2がα減っていることから、下のような表がかけます。
(反応中)は、各分子の係数比が『2:1:2』より\(-2\alpha,-\alpha,+2\alpha\)分だけ変化します。)
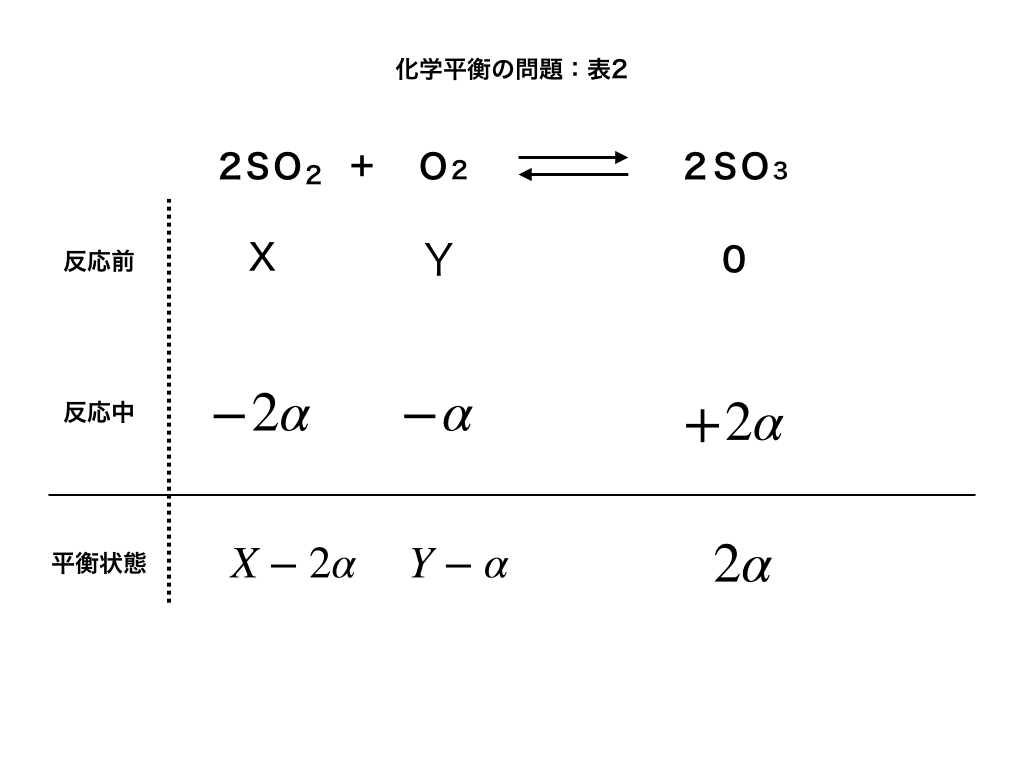
従って、\(SO_{2}=X-2\alpha ,O_{2}=Y-\alpha ,SO_{3}=2\alpha \cdots 答\)
解説(2):単位とKの公式に注意
つぎは化学平衡の問題の中でも“メイン”とも言うべき『平衡定数:Kの値』と『その単位』を求めていきます。

先ほどの、(イメージ図)と同様に計算すると、SO2とSO3は係数が”2”なので二乗し、O2は1乗することで次の(答)が得られます。
$$K=\frac{[2\alpha]^{2}}{[X-2\alpha]^{2}[Y-\alpha]}$$
\([括弧の中]は体積V分の物質量\)だったので、
$$K=\frac{\frac{2\alpha^{2}}{V^{2}}}{\frac{(X-2\alpha)^{2}}{V^{2}}\times \frac{Y-\alpha}{V}}$$
式を整理して、$$K=\frac{(4V\alpha^{2})}{(X-2\alpha)^{2}(Y-\alpha)}\cdots (答)$$
単位は、\(分母が\frac{mol}{L} の2乗×\frac{mol}{L} の1乗\)、分子が\(\frac{mol}{L} の2乗\)であるので、$$\frac{\frac{mol^{2}}{L^{2}}}{\frac{mol^{2}}{L^{2}}\times \frac{mol}{L}}$$
$$=\frac{1}{\frac{mol}{L}}=\frac{L}{mol}\cdots (答)$$
解説(3):定数の式に代入して整理
あとは、Kの式に問題文で与えられた値を代入して、計算をするだけです。
(再掲:X=4Y、\(α=\frac{Y}{3}\)としたときのKを求めよ。)と
平衡定数\(K=\frac{(4V\alpha^{2})}{(X-2\alpha)^{2}(Y-\alpha)}\)から、
$$K=\frac{\frac{4VY^{2}}{9}}{\frac{100Y^{2}}{9}\cdot \frac{2Y}{3}}$$
ゆえに、$$K=\frac{3V}{50Y} (L/mol) \cdots (答)$$
この記事:平衡のまとめ
今回の化学平衡は、(下でまとめている『電離平衡』)や『溶解平衡』・『圧平衡定数』などの基礎となるものです。
しっかりと、”普通の”平衡をマスターすることで、応用versionになった時に理解しやすくなるので、何回か復習しておいてください。
>>『反応速度と平衡の記事一覧へ』
化学平衡シリーズ一覧
関連する記事を『平衡シリーズ』としてまとめています。
(NEW!):「反応速度"v"・速度定数"k"と平衡の関係」で、正方向・逆方向の”反応速度定数”と”平衡定数”の関係や、計算についてまとめました。
「平衡のかたよりを判別!『ルシャトリエの原理』とは?」『××した時、平衡は左/右に移動するor変化しない、のいずれか?』と言った問題が非常によく聞かれます。
上の記事では、『××したら●●になる』という単なる暗記ではなく、仕組みから解説しているので、忘れにくいようになっています。ぜひ合わせてご覧ください!
「弱酸のpHを求める:『電離平衡』を解説」(応用で、酸と塩基との分野横断問題です。)
「濃度平衡定数Kcと圧平衡定数Kpの相互変換+それぞれの練習問題」
(・・・その他の平衡を現在作成中です・・・)
最後までご覧いただきまして、ありがとうございました。
「弊サイト:スマナビング!」では、読者の皆さんのご意見・ご感想等をコメント欄にて募集しております。
また、お役に立ちましたら、B!やシェアをしていただけると、とても励みになります。
・お問い合わせ/ご依頼/その他のご連絡は、ページ上部の【運営元ページ】よりお待ちしております。

