『濃度』3種類の意味と扱いかた、教えます
<この記事の内容>:高校理論化学の「溶液」分野をはじめとして、化学の様々な計算問題であらわれる『3種類の濃度』の意味と計算法を解説します。
さらに、苦手な人が多い
・【mol濃度⇄質量パーセント濃度⇄質量モル濃度】の相互変換や、
・密度との関係を理解して、
”自由自在にあやつれる”ようにするために大切な、「単位」の考え方まで紹介しています。
具体例(解説・練習用問題付き)
目次(タップした所へ飛びます)
濃度は単位に注目せよ!~3種類を攻略~
これから濃度を見ていきますが、兎にも角にも【単位】に注意することが一番大切です。
さらに言うと、単位がヒントになる事も少なくないです。
用語・単位の復習と整理
この3つは、『溶液』・『溶媒』・『溶質』のいずれが分子・分母にくるのかが大変重要です。
『溶質』:「溶媒」に溶ける物質のこと。(ex:\(CaCl_{2}\)水溶液における”塩化カルシウム”)
『溶媒』:「溶質」が溶ける液体のこと。(ex:\(CaCl_{2}\)水溶液における”水”)
『溶液』:「溶媒」と「溶質」を合わせたもの。(ex:\(CaCl_{2}\)水溶液”全体”)
(*:以下の例題では、式量・原子量を:Ca=40、Cl=35.5、H=1、O=16、Na=23、とする。)
モル濃度とは
まず初めはモル濃度から解説していきます。
単位:mol/L
「”mol”濃度」の言葉通り、以下のような式で求める事ができ、その単位は(mol/L)となります。
$$\frac{溶質の物質量(mol)}{溶液の体積(L)}$$
以下のイメージのように分子は『溶質』、分母は『溶液』であることに気をつけて覚えましょう。
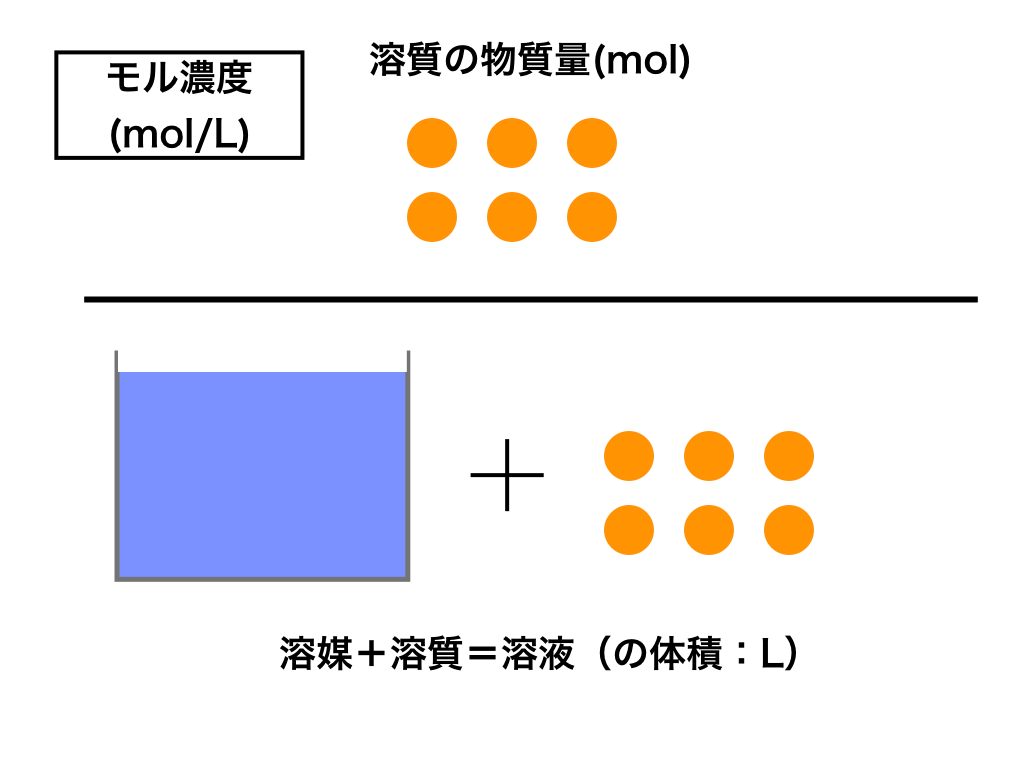
(後で登場する『質量mol濃度』と混同しがちになります。要注意!)
例題1
塩化カルシウム\(CaCl_{2}\) 333(g)を溶媒にとかして4Lの溶液を作った。この時のモル濃度を求めよ。
解説1
まず塩化カルシウムの物質量(mol)は、塩化カルシウム\(CaCl_{2}\)の質量 333 (g)÷式量 111 (g/mol)=3(mol)・・・(一)
体積は問題文ですでに4(L)と与えられているので、
結局\(\frac{3(mol)}{4(L)}\)
よって、モル濃度は
$$7.5\times 10^{-1}(mol/L)$$
シンプルですね!
質量パーセント濃度とは
次は”質量パーセント濃度”にうつりましょう。
単位:g/g→%
$$\frac{溶質の質量(g)}{溶液の質量(g)}\times 100=\%$$
これも非常に単純で、溶液の質量(g)を分母、溶質の質量(g)を分子に持って来た上で「割合」を求めます。(%であらわすために、100倍しています)
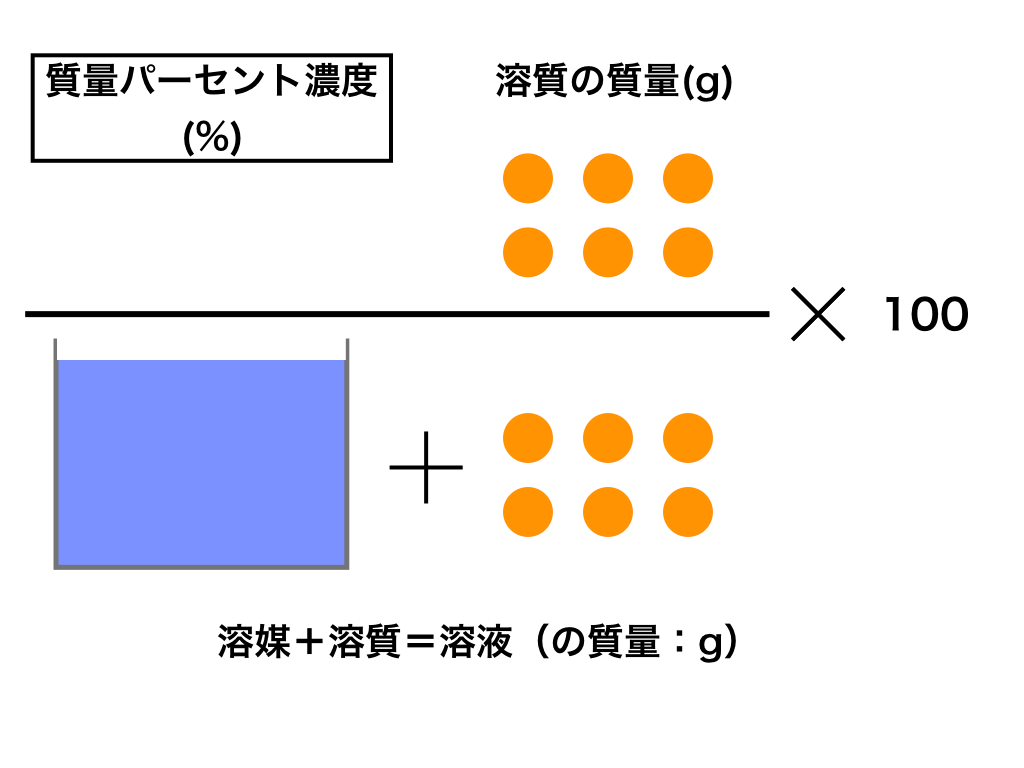
すなわち、\(\frac{溶質}{溶液}をもとめて、この値を100倍したもの\)のことを言います。
例題2
NaCl 2(mol)を水800(g)に溶かした時の”質量パーセント濃度”を求めよ。
ここでは、
step1:まず溶質である塩化ナトリウムの質量を(mol数×式量)で求め、
step2:分母は【溶液の質量】なので、溶媒である”水”の質量と”塩化ナトリウム”の質量を足し合わせます。
step3:次に、”step1で求めたNaClの質量”を”step2で求めた全体の溶液の質量”で割り
step4:パーセント(%)で表すために、step3の結果を100倍すれば終了です。
解説2
step1:NaClの式量は58.5、これが2molあるから,\( 58.5\times 2=117(g)\)
step2:溶液の質量=117(g)+800(g)=917(g)
step3:計算を進めていくと、\(\frac{117(g)}{917(g)}\)ですが、途中で割らずにstep4へ移行します。(なるべく計算は最後に持っていく)
step4:\(\frac{117(g)}{917(g)}\times 100≒0.1275\times 100=12.8\%\)
∴答え:12.8(%)
質量モル濃度とは(分母に要注意!)
注意点1:分母は『溶媒』の質量である。
注意点2:分母の単位は(Kg)である。
単位:mol/Kg
$$\frac{溶質の物質量(mol)}{溶煤の質量(Kg)}$$
見出しの通り、質量(Kg)を分母に、物質量(mol)を分子に持ってくるのが『質量モル濃度』です。
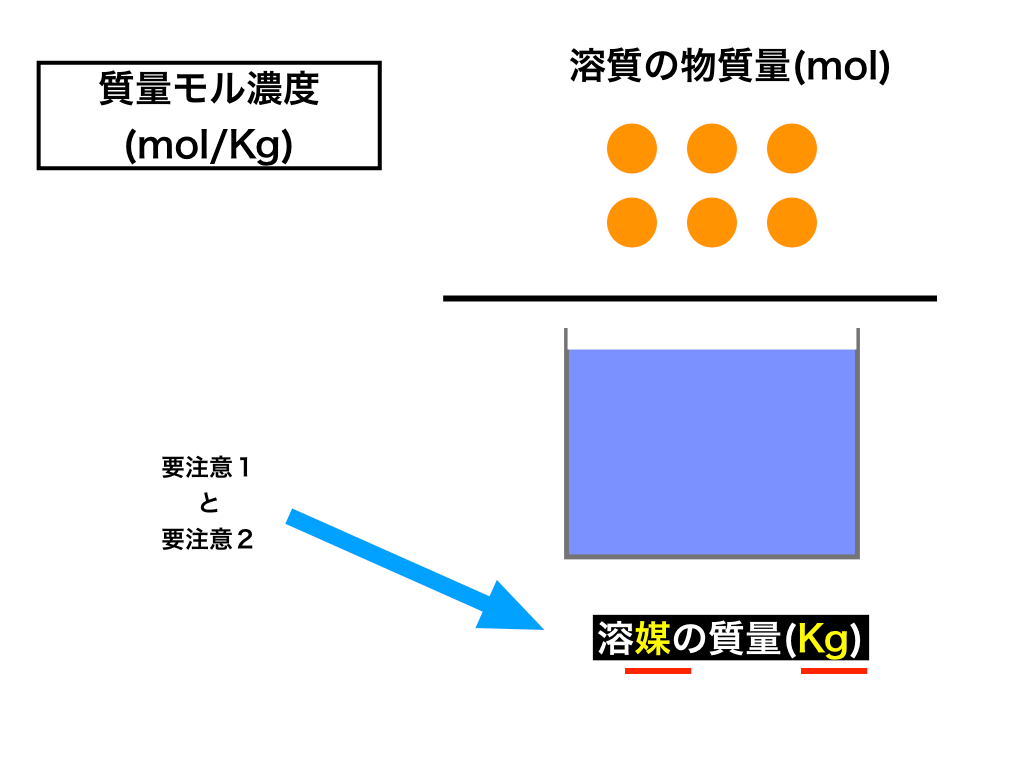
重要なのは分母が「溶液の質量」ではなく、「溶媒の質量」であると言う事です。
先ほどから繰り返して述べているように、非常にミスをしやすいので注意しましょう。
例題3
\(CaCl_{2} 55.5(g)\)を、\(H_{2}O 100(mol)\)に溶かして溶液を作った。
この時の”質量モル濃度”を求めよ。
解説3
まずは溶質(塩化カルシウム)の物質量を求めて、\(\frac{55.5}{110}=0.5\)mol。
次に溶媒の質量:\(18\times 100\times 10^{-3}=1.8(Kg)\):1800gで表されていたものをを、『Kg』に変えるために1000で割って(\(10^{-3}\)を掛けて)います。
それぞれ求めた上で、溶質分の溶媒より\(\frac{0.5}{1.8}≒2.8\times 10^{-1}\left(mol/Kg\right)\)
それぞれの濃度の変換と密度
ここからは、上で紹介した3つの”濃度”をそれぞれ別の種類の”濃度”に変換したり、密度dとの融合問題を紹介し、その解き方・コツなどを紹介していきます。
(from)質量パーセント濃度から→(to)mol濃度
問題4:質量パーセント濃度が96%、密度d=1.84\((g/cm^{3})\)の濃硫酸のモル濃度を求めよ。
(有名問題)
解答編:質量%→mol濃度
解答と解説4:
STEP1:まず、溶液全体の質量を\(密度d\times 体積V(cm^{3})\)で求めます。
すると、\(1.84\times 1000=1840(g)\)
・・・体積1000cm^{3}で計算。
STEP2:次に溶質である濃硫酸の質量を求めると、
\(全体×割合=1840\times 0.96\)
分子量は98(g/mol)なので
STEP3:mol数を計算し、
\(1840\times 0.96÷98≒18.0(mol)\)
体積1000cm^{3}=1(L)で計算を進めていたので、
18(mol/L)・・・(答)
(from)質量パーセント濃度→(to)質量モル濃度へ
問題5:密度dが1.2(g/mL)・質量パーセント濃度が40%の塩化カルシウム\(CaCl_{2}\)溶液の、質量モル濃度を求めよ。
解答編
解答と解説5:
STEP1:【密度→溶液の重さを計算】
まずはdをつかって1リットルあたりの「溶液全体」の重さを求めると、\(1.2\times 1000=1200(g)\)
STEP2:【溶質の重さを計算】
質量%が40%なので、1200(g)の内\(1200\times 0.4=480(g)\)が溶質=\(CaCl_{2}\)の重さ。
STEP3:【溶質のmol数の計算】
塩化カルシウムの式量=111なので、分子に当たる物質量は《480÷111》(mol)。
STEP4:【溶媒の重さを計算】分母の単位はKgだったので、1.2(Kg)-0.48(Kg)=0.72(Kg)。
STEP5:【溶媒1Kgあたりに変換して完了!】
0.72(Kg):《480÷111》(mol)=1.0(Kg):●(mol)
より、$$\frac{480÷111}{0.72}≒6.0$$
よって$$6.0(\frac{mol}{Kg})\cdots (答)$$
かなり計算がメンドウでしたが、はじめは『計算の流れ』に注意して(STEP1〜5)解いていきましょう。
今回の(溶液と3つの濃度)まとめ
今回解説した中でも、『単位に注目する』という考え方は極めて重要で、化学はもちろん物理でも『次元解析』などで必須です。
濃度3種類をうまく使うことに慣れるには、少々練習が必要かも知れません。
しかし、溶液・酸塩基・化学平衡など液体や気体が絡むところには必ず「濃度」が出現するので、ぜひ何度も復習しておいてください。(復習用にオススメしている参考書→「化学・化学基礎分野の演習書3選+α」)
濃度を使う問題の記事まとめ(平衡/pH/凝固点効果etc,,,)
溶液・希薄溶液に関連する分野(参考:「気体・(希薄)溶液分野の解説記事まとめページ」)で非常に頻繁に使用します。
例えば、「酸・塩基とpHの求め方、計算に必要なlogまで紹介」のようなpHを求める際には今回学習した『mol濃度』と『電離度』を使います。
(化学)電離平衡→「弱酸・弱塩基のpH(水素イオン指数)と電離平衡」も余裕があれば、読んでみてください。
また、「沸点上昇と蒸気圧降下の計算問題を解説」や「ファントホフの式と浸透圧の計算をわかりやすく」でも、質量モル濃度は必須です。
・・・etc,,,
最後までご覧いただき、ありがとうございました。
弊サイト:「スマナビング!」では、読者の皆さんのご意見・ご感想・記事リクエスト等の募集をコメント欄にて行なっております。(※:現在、個々の問題の質問に関しては対応出来ない場合があります。)
また、お役に立ちましたらB!やシェアをしていただけると、大変励みになります!
・お問い合わせ/ご依頼/その他のご連絡は、【運営元ページ】よりお願いいたします。

