インピーダンスの式の意味と導き方
<この記事の内容と対象>:高校物理の交流分野で登場する、RLC(直列)回路・インピーダンス”Z"がイマイチわからなかったり、式が複雑に見えてこの範囲を苦手としている人を対象に、数学2・3の範囲内でわかりやすく解説しています。
【準備編】で必要な数学の基本(sin,cosの微分とsin型での合成)について振り返っているので、その辺りがあやふやな人でも理解できるようにしています。
目次(タップした所へ飛びます)
インピーダンスとRLC直列回路【準備編】
ここでは、文頭にも書いたように数学的な準備とオームの法則の確認を行います。曖昧な人は各々の項で紹介しているページでよく復習してからこの記事に戻ってください。
内容をざっと見ていずれも理解できている人は次の『インピーダンスの導出(実践編)』へ進んでください。
数学的な準備(高校2/3)
準備といってもそれほど大層なものではなく、上述したように、『sin型での合成』と$$\frac{d}{dx}\sin x,\frac{d}{dx}\cos x$$ができれば全く問題ありません。
三角関数の諸公式と合成
<ここに合成の図を入れる>
なぜそうなるかは「三角関数の『合成と加法定理』意味が理解できる解説記事」をご覧ください。
(三角)関数の微分・合成関数微分
\((\sin x)'=\cos x ,(\cos x)'=-\sin x\)
あとは、『\(\sin \omega t をtで微分する\)』といったことを行うので、「合成関数の微分の仕方を紹介」を必要に応じて参照してください。
オームの法則の復習
あとはオームの法則です。インピーダンス”Z”については、高校レベルでは『交流回路における抵抗』のようなもの、と考えると楽なので、直流回路における(電圧・電流・抵抗の関係を表す)オームの法則と比較して考えていきます。
念の為確認しておきましょう。
\(V=IR\)
V:電圧(単位V)・I:電流(単位A)・R:抵抗(単位Ω)
インピーダンスの式の導出【実践編】
RLC直列回路の”インピーダンス”を求める為に、まずはR(抵抗)・L(コイル)・C(コンデンサー)それぞれと電源(交流)をつなげた回路での、電流・電圧・(抵抗)の様子を見ていきます。
(ここでは、交流電源の最大電圧を\(V_{M}\)、最大電流を\(I_{M}\)とし、電流は\(I=I_{M}\sin \omega t\)で表すことにします)。
(一般的に最大電圧・電流を\(V_{0},I_{0}\)と表記するのですが、MaxのMの方が初学者には一見して最大と分かりやすい場合がある為,このようにしています。)
Rにおける抵抗値
まずは最も簡単な、交流電源と抵抗を一つ接続した場合を考えます。
\(V_{M}\sin\omega t=I_{M}\sin\omega t \cdot R\)
checkするところは、位相のずれ\((\sin ωt)\)が無いことと、R(Ω)がこの回路における抵抗の役割をしている点です。
L(コイル)における自己(誘導)インダクタンス
次はコイル(L)と交流電源の回路です。コイルには、「電流が流れることによって”磁界が発生する”」という特徴があり、”急激な電流の変化を妨げる”方向に電圧が生まれる『自己インダクタンス』という性質があります。
インダクタンスには、『2つのコイルが影響を及ぼしあう、相互(〃)』と『自己(〃)』がありますが、ここでは自己〜を使用します。
$$起電力の公式:V=-L\frac{\Delta I}{\Delta t}$$
ただし、L(H)は単位ヘンリー。
ここで回路図を見ると、交流電源とコンデンサーは閉回路でつながっていることから、キルヒホッフの法則より、\(V_{交流電源}+V_{コイルによる起電力}=0\)が成り立ちます。
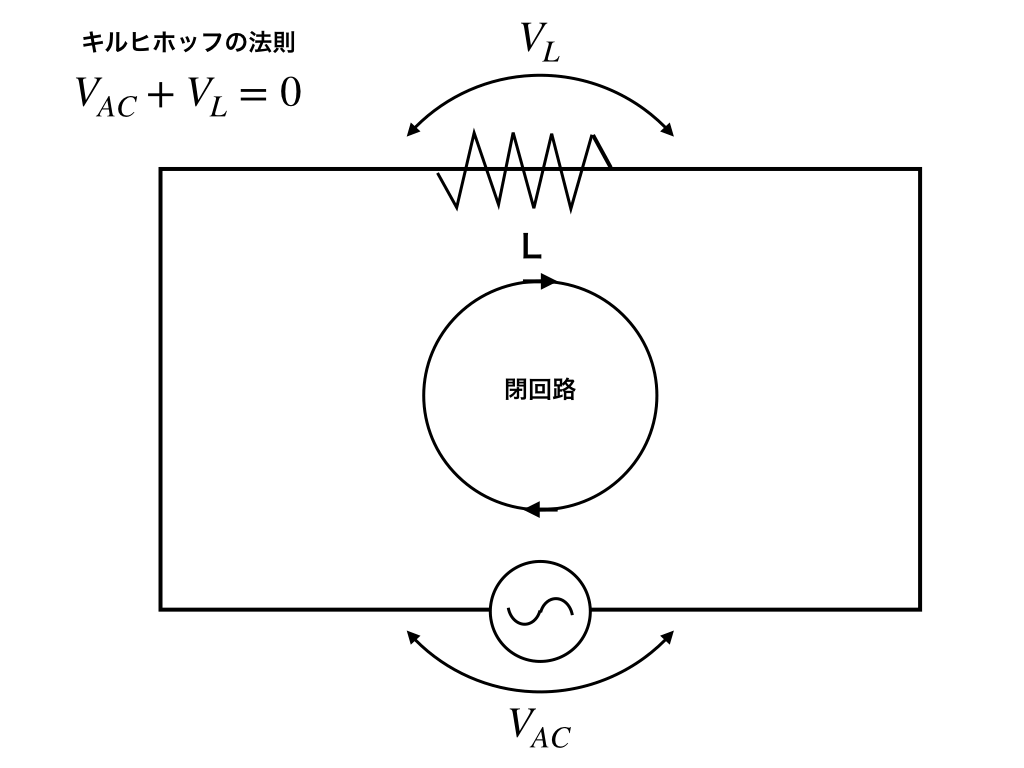
\(I=I_{M}\sin\omega t \)を上の公式に代入すると、\(V_{コイル}=-L\frac{d}{dt}I_{M}\sin\omega t\)
微分すると、\(\sin\rightarrow \cos に変化し、\omega\) が一つ前に出るので、\(V_{コイル}=-L\omega I_{M}\cos\omega t \)さらに、これを\(V_{電源}+V_{コイル}=0\)に代入することで、
マイナス×マイナスとなって、\(V_{電源}=-V_{コイル}=-(-L\omega I_{M}\cos\omega t )\)
つまり、\(V_{電源}=L\omega I_{M}\cos\omega t \)となります。
オームの法則と比較(L ver)
見出しの通り、求めた電源の電圧の式とV=IRを見比べてみます。
\(V_{電源}→V\)、
\(I_{M}\cos\omega t →I \)なので、
Rに相当する部分が→\(L\omega\)であることが分かります。このLωを”誘導リアクタンス”と呼んでいます。
位相のズレのチェック(L ver)
\(V=V_{電源}=V_{M}\sin\omega t \)であったことと、\(V_{電源}=(L\omega )I_{M}\cos\omega t \)を見比べて代入すると、\(V_{M}\sin(\omega t)=(L\omega )I_{M}\cos(\omega t)\)
$$I_{M}\cos\omega t=I_{M}\sin(\omega t +\frac{\pi}{2})$$
一方、電圧は\(V_{M}\sin\omega t \)となっていることから、I(電流)を基準にすると、Iがπ/2だけVより「遅れている」、という事が確認できます。
少し数式が増えてきて大変だと思いますが、ココは最後の【インピーダンスの計算】の際に重要になるので、しっかりと自分で理解し、式変形まで出来るようになっておきましょう。
C(コンデンサー)における容量リアクタンス
さて、RLC回路を構成する最後の一つ『コンデンサ』についてこれまで同様に見ていきます。
「コンデンサーの基本的な公式」の中で、ここで使うのは『Q(単位C:電気量)=V・C(単位F:電気容量)』と、「電流”I=envS”の基本」である”電流は時間あたりに通過する電気量に等しい”というものの2つだけです。
\(I=\frac{dQ}{dt}\)、Q=CV、\(V=V_{M}\sin\omega tより、VにV_{M}\)を入れて微分すると、
$$I=\frac{d}{dt}CV\sin(\omega t)=C\omega V\cos(\omega t)$$
ここで、\(-1≦\cos\omega t ≦1\)より、cosの最大は1でその時、電圧が最大となるので\(cos\omega t=1\)を代入して整理すると、\(V_{M}=\frac{I}{C\omega }\)の式が出てきます。
オームの法則と比較(C ver)
さらにコイルの際にも行ったオームの法則との比較を行うと、
V=IR
’$$V_{M}=I\frac{1}{C\omega }$$
より、Rに相当する部分は『1/ωC』であることが分かります。
位相のズレのチェック(C ver)
最後にVとIの関係を確認すると、
$$I=\frac{d}{dt}C=C\omega V\cos(\omega t)$$
\(I=C\omega V\sin(ωt +\frac{\pi}{2})\)
\(I=I_{M}\sin(\omega t)だから、\)
I(電流)が電圧よりもπ/2だけ「進んでいる」ことが分かります。(コイルの時と逆の結果です!要注意)
”RLC直列回路”におけるインピーダンス【結論編】
ここまでくれば、あともう一息でインピーダンスを求めることができます。
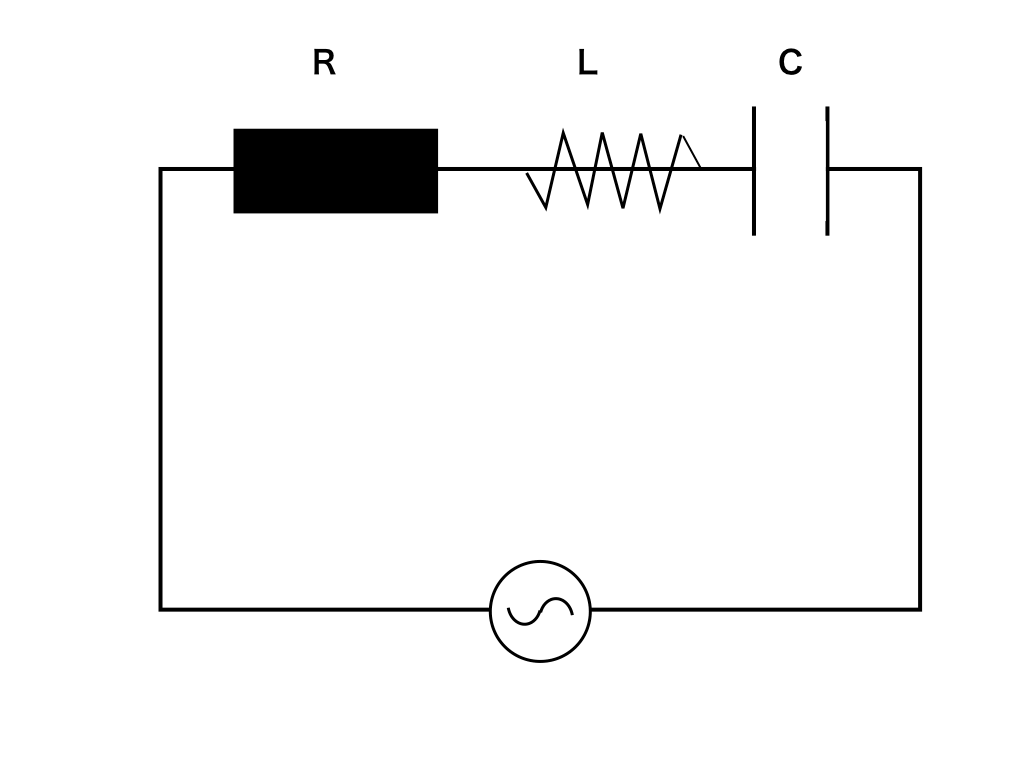
交流電源にRLCを【直列】に接続した時のインピーダンス【Z】は「抵抗」のようなものなので、(直列→電流が同じ)より、R・L・Cそれぞれにかかる電圧を合計すると、V=IRのカタチになって“Z”を求めることができます。
三角関数の種類と位相をそろえる
ただし、実はインピーダンスは周期的に電流の向きが変化する交流回路ゆえに(位相が異なるので)、直流の場合のような単純な(スカラー量)での足し算では計算できません。
そこで次のように電圧を足し合わせていきます。
‘$$V=I_{M}Lω\cos\omega tーI_{M}\frac{\cos\omega t}{C\omega }+R\ sin(\omega t)$$
(※)注意:Iを基準にしているのでコンデンサーはπ/2遅れる→符号がマイナスになっています。
上の式をI_{M}でくくってcosωtの係数を足し、sinとcosだけの式を作ります。
$$I_{M}[(Lωー\frac{1}{C\omega })\cos\omega t+R\sin(\omega t)]$$
最後にsinとcosを揃えればインピーダンスZと位相が出てくるのですが、どうすれば良いでしょう?
・・・もう分かっているかと思います。「三角関数の合成」ですね!
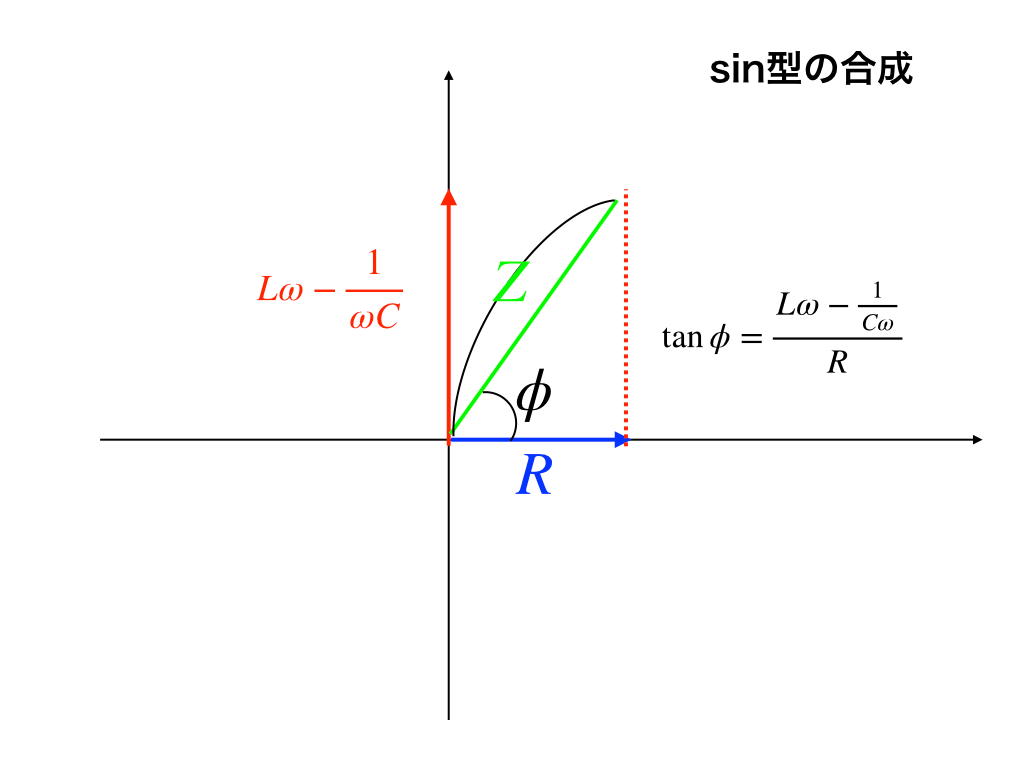
図を描いて、
$$Z=\sqrt{R^{2}+(Lωー\frac{1}{C\omega })^{2}}$$
$$\phiは\tan\phi とし=\frac{Lω-\frac{1}{ωC}}{R}$$
このようにしてZと位相Φが求まりました。
・・・計算も大変で、行っている式変形や意味もかなり難しかったかと思います。次の項でまとめている順番に復習しておきましょう。
多少つまるところがあるかもしれないですが、慣れてくるまで諦めずに頑張ってください!
インピーダンスのまとめ
・まずは、R/L/Cそれぞれ単体と交流電源をつないだ場合のIとVの関係式・リアクタンスなどを公式の微分で説明できるように復習しましょう。
・次に、RLC直列回路におけるインピーダンスZの式を、三角関数の合成を使って求めます。
・後は、RL/LC/RCの2つの直列や、並列回路の問題を問題集:(オススメは>>物理の問題集5選『標準〜最難関レベルまで』)などで解いて知識を定着させましょう。(一度インピーダンスを導くことができれば、必ず解けるようになっています!)
関連記事と続編(電気振動)へ
(交流分野第一回):「(今ココです)RLC(直列)回路とインピーダンス”Z”」
(交流分野第二回):「共振と電気振動・LC回路をわかりやすく!」
(交流分野第三回):「(作成中)交流の定着・確認問題」
最後までご覧いただきまして、有難うございました。。
”スマホで学ぶ”『受験・学習メディア「スマナビング!」』では、読者の方のご意見、ご感想・誤植の指摘などをコメント欄にて募集しています。
(※:個々の問題の解き方については対応できない事がございます。ご了承ください)
・その他のお問い合わせ/ご依頼等につきましては引き続き受け付けています。
【運営元ページ】よりご連絡をお願いします。

