
接線とグラフ・軸が囲む面積と体積
<この記事の内容>:前回「接線の方程式の求め方と接点が未知の場合の対処法」の記事で、接線の求め方などを詳しく紹介しました。
今回はその続編として、
・その『接線と関数のグラフ、軸などに囲まれた部分の面積』をうまく求める方法を解説し、
・さらに、その部分を回転させた時の体積の求め方まで紹介していきます。
目次(タップした所へ飛びます)
グラフとその接線によって囲まれる面積
前回と今回の内容はセットで出題されることが多く、標準レベルの大学入試では特に頻出です。
(難関大はさらに設定を複雑にしたり(ex,別分野との融合)、計算量が膨大になる様にしてきますが、基本がしっかりしていれば、それらの問題も解ける様になっていきます)
具体例で手順を確認【理解編】
問題1:\(y=e^{x}のグラフ(C_{1}とする)\)と\((3,e^{3})\)で接する接線の方程式(これを\(l_{1}\)とする。)を求め、\(C_{1},l_{1},x=0(y軸)\)で囲まれた部分の面積を計算せよ。
解答解説
前回:「接線の方程式の求め方と接点が未知の場合の対処法」解説した接線の求め方の手順通りに、接線の傾きを\(f(x)=e^{x}\)を微分して求め、接点を代入します。
\(f'(x)=e^{x} ,(3,e^{3})\)を通るので、\(l_{1}:y=e^{3}(x-3)+e^{3}\)次に、囲む面積をSとすると、次の<図1>の部分なので、
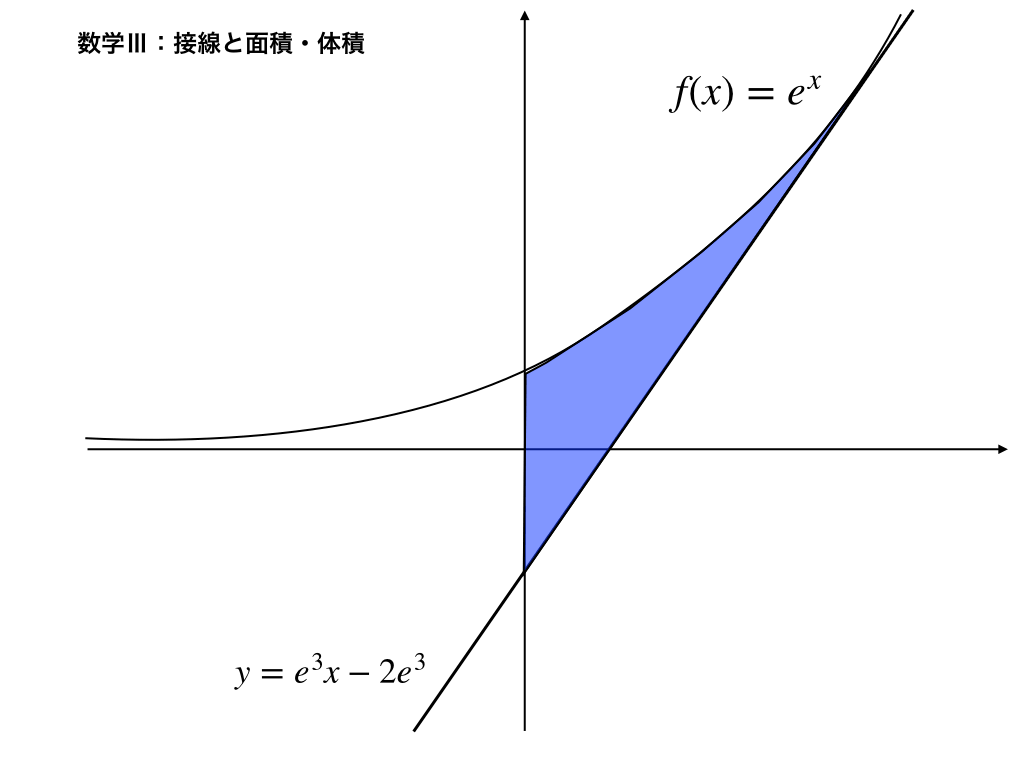
<図1>
$$S=\int^{3}_{0}e^{x}-(e^{3}x-2e^{3})dx$$
よって、$$S=\frac{5}{2}e^{3}-1・・・(答)$$
面積・体積を求める問題とコツ【実践編】
次に、実践的な問題を通して流れとポイントを見ていきます。
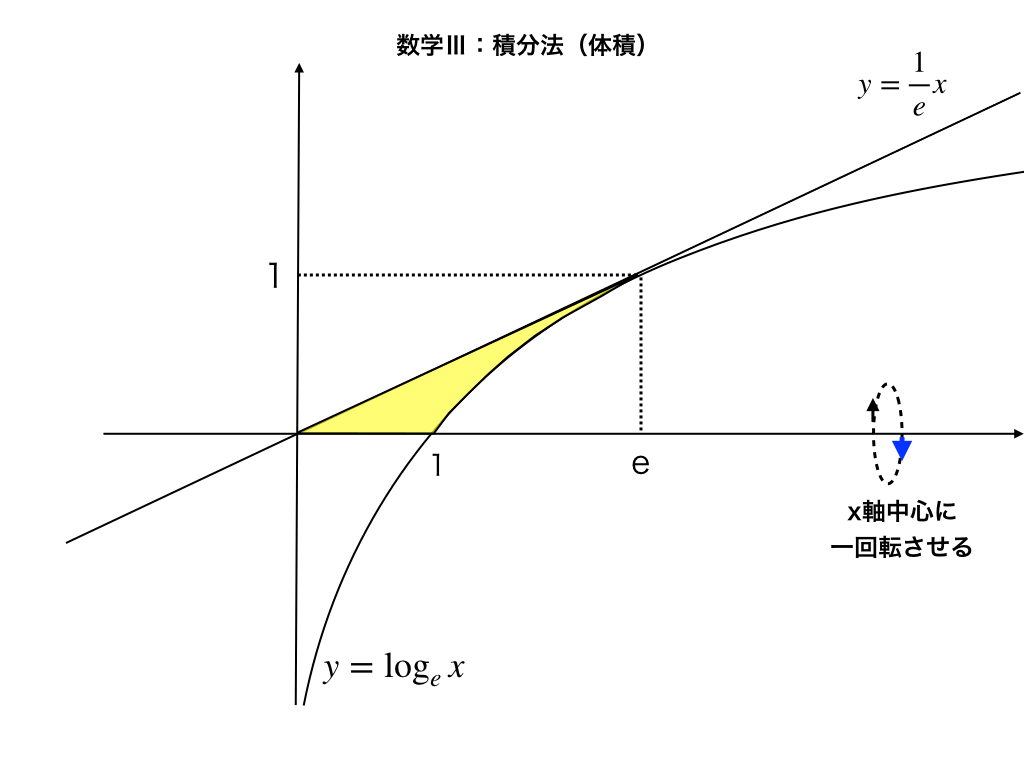
問題2-1:\(y=\log{x}\)に接し、\((0,0)\)を通る直線の方程式\(l_{2}とy=0(x軸),y=\log{x}\)に囲まれた部分の『面積』を求めよ。
問題2-2:2-1で求めた部分を『x軸を中心として』一回転させたとき、その回転体の\(体積V_{1}\)の値を求めよ。
問題解説2:(面積)計算を楽にするポイント
今回は特に使用しませんが、面積計算の問題が出た場合には、常に「偶関数と奇関数とは?その面積計算への応用」や「有名な面積公式:1/6,1/3,1/12などを紹介」を意識して計算量を減らすことが出来ないか?を考えておきましょう。
この場合は接点の座標がわからないtypeなので、接点を文字でおき:\(点T(t,\log{t})\)
次に、点Tでの\(f(x)=\log{x}\)の傾きを求めます。$$f'(x)=\frac{1}{x},より,f'(t)=\frac{1}{t}$$
これと、\((t,log{t})\)を通ることより、接線\(l_{2}\)の方程式は$$y-\log{t}=\frac{1}{t}(x-t)$$
\(l_{2}\)が(0,0)を通るので、\(0=\log{t}-1\) よって\(t=e\)
$$l_{2}:y=\frac{1}{e}・・・(答1)$$
次に、求める面積をS’とすると、$$S'=\int^{e}_{0}\frac{1}{e}x dx-\int^{e}_{1}\log{x}dx$$
で計算することができ、結果$$S'=\frac{e}{2}-1$$が答えとなります。
(途中の\(\log{x}\)の積分は、部分積分をする(参考:「部分積分の仕方とコツ」)ことで\(x\log{x}-x\)と計算できます。
問題解説2:体積の求め方
体積Vは、\(l_{2}\)をx軸周りに一周した結果できる円錐から、\(\log{x}\)を回転させてできるたけのこ状の物体の体積を引いて求めます。
「(現在作成中です)体積の計算法(数Ⅲ積分法の応用)」
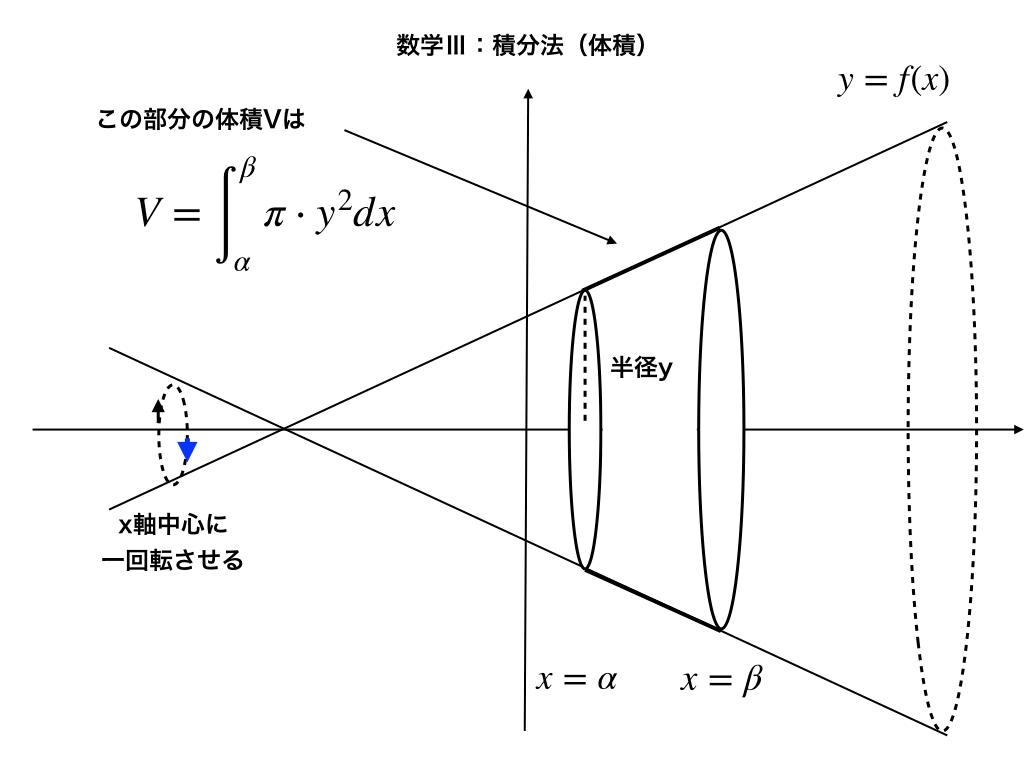
より、y=f(x)のグラフをx軸周りに回転させてできる物体の体積Vは$$V=\pi\int^{\beta}_{\alpha}y^{2}dx$$なので、
$$\pi\int^{e}_{0}(\frac{x}{e})^{2}dx-\pi\int^{e}_{1}(\log{x})^{2}dx$$
これを計算すると、(※:途中\((\log{x})^{2}\)は部分積分を二回行います)
$$V=2\pi-\frac{2e}{3}\pi・・・(答)$$
と求まります。
この記事のまとめと続編へ
この記事では、接線の方程式と簡単な指数・対数関数のグラフを囲む面積+体積の求め方を紹介しました。
特に体積に関しては、x軸について回転させるだけでなく、y軸の周りを一周させる場合など何種類かパターンがあります。
次回の記事で様々な求積法とテクニック(バームクーヘン分割・傘型分割etc,,,)を詳しく見ていきます。(以下にまとめています。)
微積分とその応用・関連記事まとめ
「(今ここです)接線とグラフが囲む面積・体積」
>>「様々な回転体・非回転体の求積法をわかりやすく!まとめ」<<
最後までご覧いただきまして、ありがとうございました。
”スマホで学ぶ”受験・学習メディア:「スマナビング!」では、読者の皆さんのご意見・ご感想・誤植の指摘などの募集をコメント欄にて行なっています。
(※:現在、個々の問題の解き方については対応できない事がございます。ご了承ください)
・その他の「お問い合わせ/ご依頼」などにつきましては引き続きお待ちしております。
【運営元ページ】より、ご連絡をお願いします。

