電流とは?I=envsの意味からオームの法則の導出までスムーズに解説

電流の意味と式〜オームの法則まで

＜この記事の内容＞：前半では、高校電(磁)気分野の基礎の基礎である『電流』の定義とイラストを用いながら「I=envS」の公式の導き方などを紹介していきます。

後半では、例えを用いてオームの法則と抵抗値について解説していきます。

＜関連まとめ＞：「高校物理・電磁気の解説記事まとめページ」

電流とは

電流は高校物理（電磁気）において、電圧や抵抗とともに電気回路の基礎から、電磁気力、電気振動、交流まですべての分野で登場する最も基本的な概念の一つです。

電流の定義と単位

電流は、『単位時間当たりに流れる(電子などの)電荷の量』で、$$I(A＝C/s)＝\frac{Q(C)}{t(s)}$$ と定義されます。

A:アンペア＝C（クーロン）÷単位時間(秒)

I＝envSの式の導出

ここからがよくテストでも問われるI=envSの式の導き方についての解説です。

まずそれぞれの文字の意味と単位を確認しておきます。

I:「電流(A)」

e:「電気量(C)」

n:「電子の密度(個/m^3)」

v:「電子の速さ=1秒あたりに電子が動くキョリ(m/s)」

S:「導線の断面積(m ^2)」

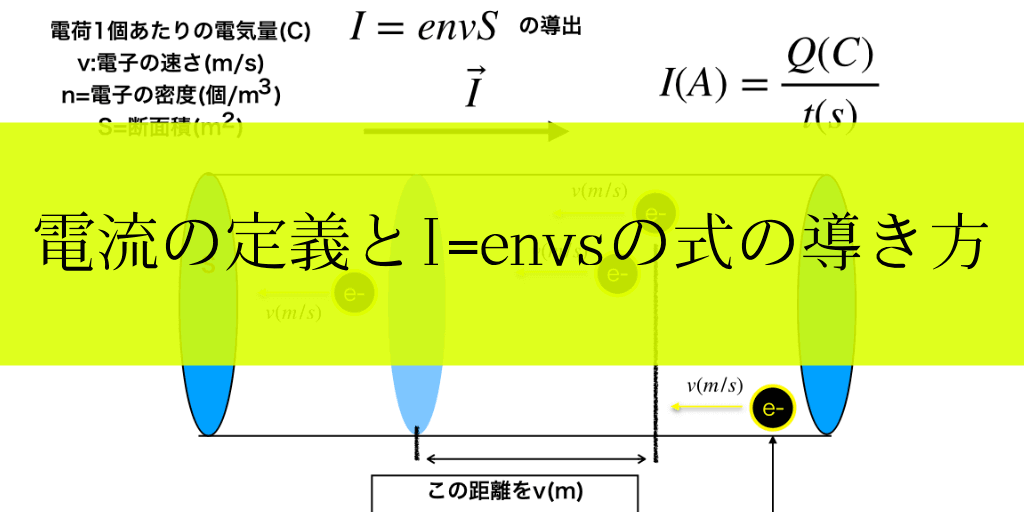
以下の＜図１＞は、"導体"で動く電荷は"自由電子"です。それでは図を見ながら導出していきます。

＜図１＞

まず、単位時間(ここでは１秒)当たりに断面積を通過する電気量:「電子の個数」が電流でした。

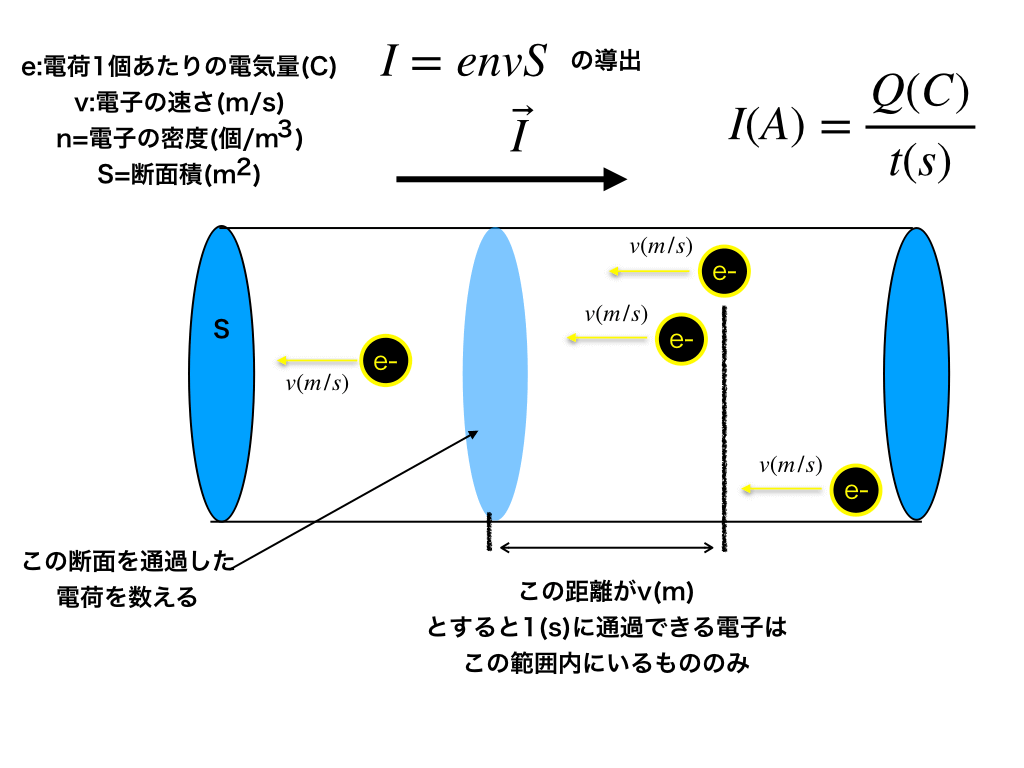
＜図1＞中の断面をギリギリ通過できる電子は、v(m)右にいる電子(１秒後にv(m/s)・1(s)進む)である事から、断面からv(m)の空間中にある電気量(C)＝(e-の総数)を求めればI(A)が計算できます。

(従って、図２の右端にある電子は断面を通過できません。）

＜図２＞

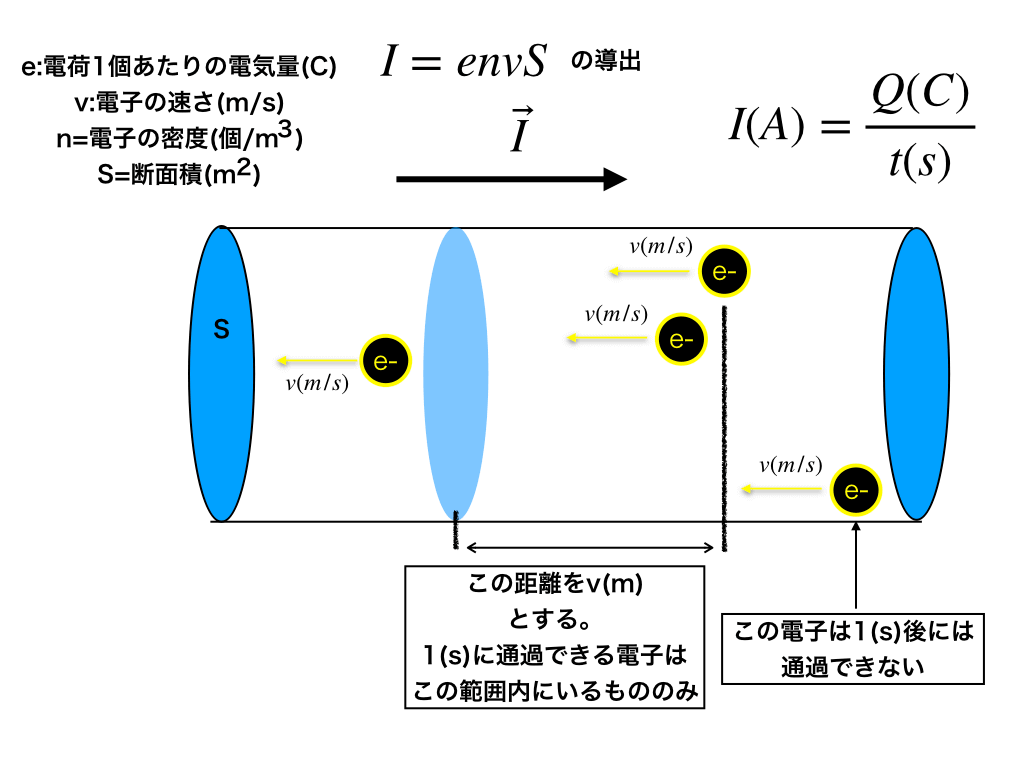
そこで、v・S＝体積と、n(電子の密度)を掛け合わせると電子の総数が求まり、さらに電子1個あたりの電気量×電子の総数＝電気量となります。

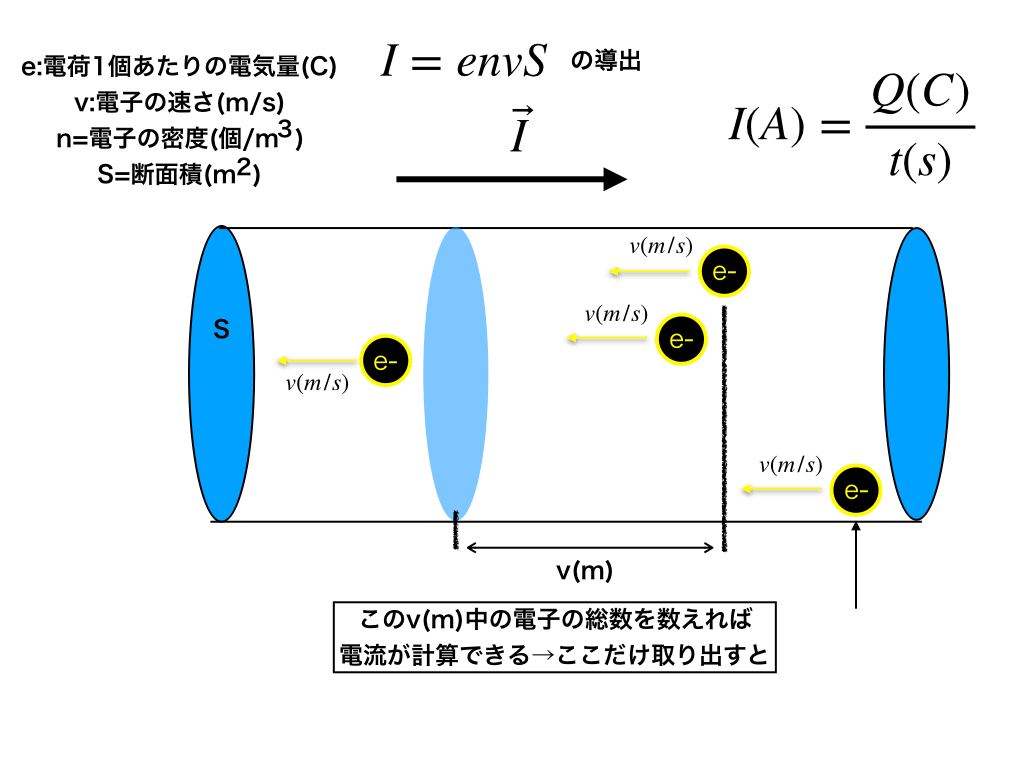
上の＜図３＞の中から、一秒後までに断面を通過する電荷（自由電子）があるところを取り出してみます。

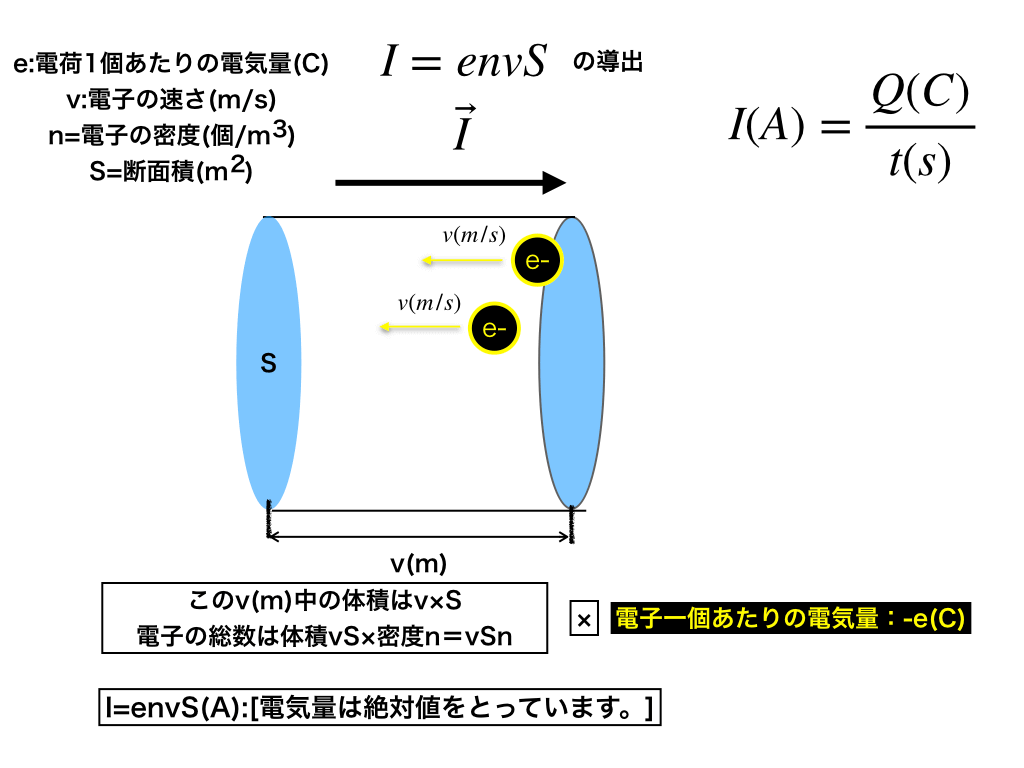
ゆえに、”１秒後までに通過する電気量＝vSne”を並べ直した”envS”が電流となり、$$I=envS$$が導けました。

電子と電流が逆向きの単純な理由

さて、ここまでで【電流の向き】と電子の移動する向きが逆になっていました。

(化学の電池・電気分解の分野:「（参考）電池と電気分解がわかる！」でも同じく紛らわしいので気をつける必要があります。)

では、何故わざわざ向きが逆になっているのかというと、単純に電流の方が発見された時代がはやく、その当時 +→−へ流れるだろうと決めてしまったからです。

それから年が経ち、トムソンら複数の科学者によって電子は発見されましたが、その時すでに電流は +極→−極へ流れると定着していた為、電子の向きと電流の向きをそろえられず今に至る、というわけです。

オームの法則

電流I＝envsを解説したので、つぎは電流Iと電位差V、抵抗値Rを結ぶオームの法則に入ります、

$$I=\frac{V}{R}$$

※非オーム抵抗の記事を新規に作成しました。「非オーム抵抗の問題とグラフの交点が答えになる理由を解説」もしくは記事下のリンクからご覧ください。

オームの法則の式の意味

この式が意味することは、

・電位差Vが一定のとき、抵抗が大きいほど電流は小さくなる。$$\frac{V一定}{R大}=I(小)$$

・逆に電位差一定で、抵抗が小さいほど電流が大きくなる。$$\frac{V一定}{R大}=I(大)$$

抵抗値Rが一定の時は

・電位差が(大きい/小さい)ほど電流は(大きく/小さく)なる

$$\frac{V大}{R一定}=I(大),\frac{V小}{R一定}=I(小)$$

という事を言っているだけです。

「電位と電場の違いを解説」でも一部紹介しているのですが、『電位＝高さ』、『電流は電位が高いところから低いところまで流れる水』、『抵抗値はその水流が通る管』と考えると理解しやすいです。

(この例えは色々な所で使われているので、聞いたことがあるかもしれません)

抵抗値が変化する要因と抵抗値の式

抵抗値の式

まずはじめに抵抗値Rの値をあらわす式を載せ、そのそれぞれの文字の意味の解説をしていきます。

$$R=\rho \frac{l}{S}(lは長さ，Sは断面積，\rhoは抵抗率)$$

R(Ω)は以下の要因で変化します。

(1):「抵抗の長さ」とRの値

式中のlの部分です。管が長ければ長いほど水流(電流)は流れにくく、大きな抵抗となります。

(2):「抵抗の太さ」とRの値

式中のSの部分です。断面積が大きい(太い)管であるほど水は大量に流れ(＝電流大・抵抗値小)、

断面積が小さい(細い)管であるほど、水は少ししか流れない(＝電流小、抵抗値大)というイメージです。

(3):「抵抗率ρ(ロー)」の意味とRの値

ρはその抵抗の材質などによって、自由電子の動きやすさが異なる(電導性の高い銀などはρが小さく、逆に殆ど電気を通さない材料で出来ているとρは非常に大きくなります)ため、それを数値化したものです。

まとめと電磁気の続編へ

・今回は電流の定義をマクロ（I=Q/t）とミクロ（I=envS ）の両方から紹介しました。

・冒頭でも述べましたが、『I=envS』を導出させる問題は”超頻出”なので、丸暗記（語呂合わせなど）をせず、必ず銅線上を電子がたくさん動いて断面を通過するイメージを理解しておきましょう。

・オームの法則と抵抗値の公式も、ただ暗記するのではなく水の流れや管と関連付けて理解することで忘れにくくなります。

・次回は、抵抗値が温度によって変化する仕組みと、苦手な人が多い『非オーム抵抗』の問題の解き方について紹介します。

・高校範囲の「電磁気分野の解説記事を総まとめ！」を作成しました。

電気分野の関連記事と非オーム抵抗の解説記事へ

続編＞＞「非オーム抵抗の問題の解法とグラフの交点が答えになる理由を徹底解説！」＜＜

＜第３回＞「キルヒホッフの第一・第二法則と回路問題の解き方」

＜第４回＞「コンデンサーを含む回路の問題の解法と注意点」

「電位と電場の違いをイメージと式で理解する」

「コンデンサーの公式と仕組みを解説！」

「コンデンサーの電気容量が変化する原因４つとは」

今回も最後までご覧頂き、有難うございました。

当サイト「スマナビング！」では、読者の皆さんのご意見・ご感想をコメント欄で募集しています。

また、 お役に立ちましたらSNSでシェア等をしていただけると励みになります。

・その他のお問い合わせ/ご依頼に付きましては、運営元ページからご連絡下さい。