
0からはじめる統計学シリーズ第1回
<このシリーズについて>:この”0から始める統計学”シリーズでは、特に機械学習の理論を知りたい方や「統計学」そのものを学びたい方の為に、中学/高校レベルの数学を復習しながら解説していきます
<今回の内容>:統計学の導入として、基本的な用語の解説や今後学ぶ分野・順序を紹介していきます。
目次(タップした所へ飛びます)
統計学のイントロダクション~何をどの順に学ぶか~
一口に統計学といっても、範囲は膨大ですし、応用する分野も多岐にわたります。
ここでは入門レベルの方が、これからこのシリーズで学ぶ分野の順序や名前、それぞれの大雑把な意味を紹介します。(※:厳密な定義や考え方などは今後一歩一歩続編で解説していきます)
また、当サイト内で中学・高校生向けに作成している内容で今後必要になる範囲の記事についてリンクを貼っているので、適宜ご利用ください。
(記事数が増えているので、まとめ記事を作成予定です2020年3月25日)
作成しました→(NEW:「統計学の解説記事まとめ」)
今後の学習の順番と、これまでの基礎的な数学との関係を以下に示しておきます。
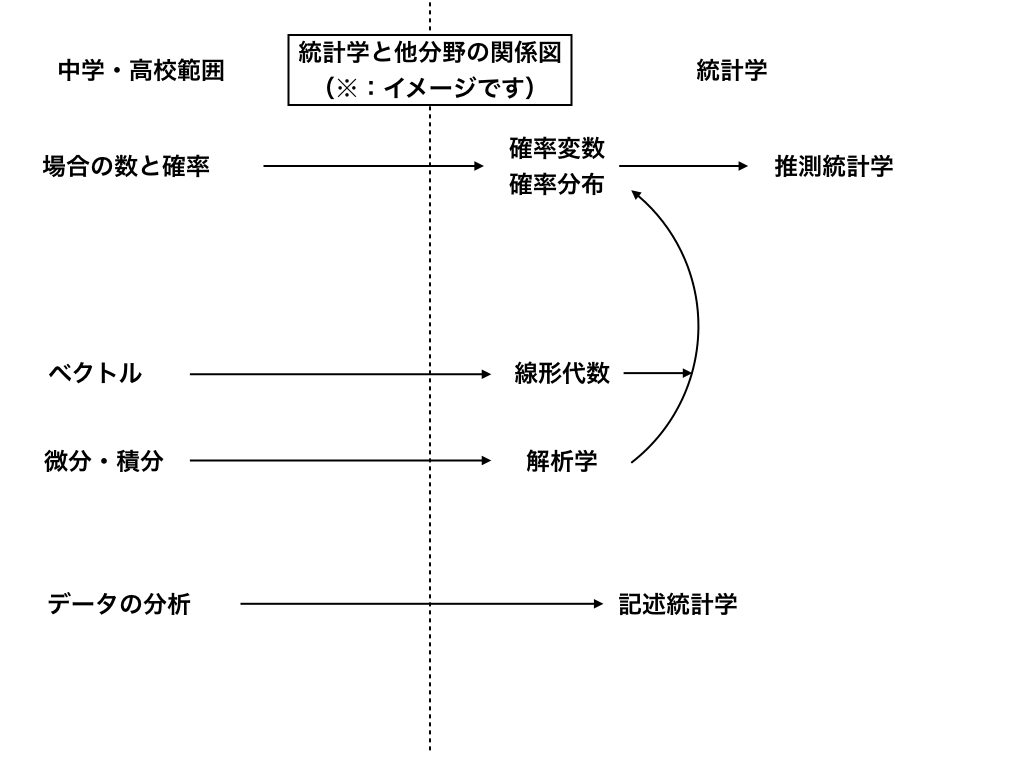
<中学・高校数学と統計学の関係図>
※:「機械学習を理解するための数学・統計学まとめ」<<の記事では、より詳細にそれぞれの単元について解説しています。
確率(・場合の数)
確率は統計学を学ぶ上でなくてはならないものです。
次回以降解説していきますが、『確率分布』や『確率密度関数』等々、、しかし、確率が苦手だった方は少なくありません。
そこで、「場合の数と確率を分かりやすく解説!記事まとめ」
上の記事に高校・大学受験レベルまでの内容をほぼ全てまとめました。
必要な知識が欠けている部分があれば見直しておきましょう。(特に確率の基礎4記事と、条件付き確率、反復試行、二項定理など)
記述統計学
まず始めに、統計学は『記述統計』と『推測統計』と言う2分野に分かれます。
記述統計学は、既に持っているデータを分析する学問です。
現在の『高校数学1:データの分析』でもその一部が教えられています。
例えば100人のクラスで行われたテストの点数のデータから、代表値と呼ばれる値(具体的には、『平均値』・『中央値』・『最頻値』などです)や、分散、偏差、などを求めて整理します。
高校範囲とかぶるので、
を先に見ておくことで、今後でてくるキーワードがスッと理解しやすくなるはずです。
推測(推計)統計学:推測と検定
次に、推測統計学(あるいは『推計統計学』)はその名の通り
・集めたデータ(これを標本という)から全体(母集団という)を推測する「推定」と、
・何らかの仮説を立ててそれが正しいか、正しくないかを判定する「検定」に分かれます。
『推定』が必要なわけ
記述統計の項で例で挙げたように、100人のクラスの成績くらいならば、全員のデータを集めて正確に分析することができます。
では次のような場合はどうでしょう。
【全ての日本人のうち、『犬』が好きな犬派と『猫派』の割合を調べたい。】
記述統計では1億2千万人以上のデータが必要になり、更にそれを分析しなければなりません。
しかしながら、当然そのような調査は不可能です。
そこで、「推測統計」では、実際の日本人の人口よりはるかに少ない標本を調査して、そこから母集団(ここでは全ての日本人)の「犬派と猫派」の割合を『推測』するのです。
勿論、全員を調査したわけではありませんから完璧な結果は出ませんが、(その派閥の割合を区間で推定することで)誤差も考慮に入れた統計的に意味のあるデータを得られることになります。
検定とは何か
「推測(推計)統計学」の内のもう一方の『検定』とは何でしょうか。
順序としては上の《推定》を先に学ぶことによって理解しやすいので、ここでは簡単に触れておくだけにします。
検定とは:
ある仮説を立てて、統計学的にそれが違っているか(このとき『棄却される』と言います。)どうかを調べること。
次回:確率変数/分布へ
次回からは、統計学で最も基本的かつ必要不可欠な『確率変数・確率分布』について詳しく紹介していきます。
(先ほどの『関係図』でまとめたように、確率分布→推計統計学、の順に進めていきます。)
関連記事と続編へ
統計学第1回:「(今ここです)統計学のイントロダクション」
第二回:「推測統計で使う『確率分布』の基礎を解説」
第三回:「ベルヌーイ分布と二項分布」
>>「機械学習の理論を高校レベルから理解する!解説記事まとめ」<<
>>「データの分析・統計学入門のカテゴリーへ」<<
今回も最後までご覧頂き、有難うございました。
当サイト「スマナビング!」では、読者の皆さんのご意見や、ご感想の募集をコメント欄にて行なっています。(※:全てに返信できない場合があります。ご了承ください。)
また、 いいね!やB!・シェア、等をしていただけると励みになります。
・その他のお問い合わせ・ご依頼に関しましては、【運営元について】のページからご連絡下さい。

