
集合と写像
論理と集合の分野は、高校数学でもあまり重要視されなかったり、いまいちよくわからないまま通り過ぎられることの多い分野です。
しかし、実際には「論理と集合」を理解していないと解けない問題は難関大学を中心に沢山出題されています。
また、「集合」と「写像」については、今や入試対策のみならず機械学習などに必須の「線形代数学」を理解する上で無くてはならないものです。
この記事では、前半で集合の考え方を、後半で集合と写像(単射・全射・全単射)について解説しています。
高校生、受験生だけでなく社会人で線形代数を学び始めたい方も、ぜひじっくり読んでみてください。
目次(タップした所へ飛びます)
集合とは何か
「明確に定義できるもの」の集まりの事を、「集合」と言います。
これでは少し分かりづらいので、例を挙げてみます。
(例)「1以上20未満の3の倍数」を考えてみると、3,6,9,12,15,18となります。
これは、誰からみても「はっきりと=明確に、定義されている」と言えるでしょう。
仮にこれを集合Pと名付けることにします。
集合になれないもの
一方で、「小さい数」ではどうでしょうか?何をもって「小さい数」とするかは人それぞれです。
このような「明確な定義」がないものは集合になりません。
要素と集合
先ほどの集合Pを構成する、3、6・・・15、18の事を、集合Pの「要素」と言います。
これを記号で3∈P、6∈P・・・のように表します。「3∈P」は「3は集合Pに属する」の意味です。
つまり、3は集合P の要素であると言う事です。
次に、この集合Pに属する要素をまとめて記述する方法を紹介します。
要素の表記法
最も分かりやすいのは以下の方法です。
(一):P={3,6,9,12,15,18}
しかしこれでは、要素の数が多くなった時に書ききれなくなり、不便です。
(二):そこで、P={x|x=3m(mは自然数),1≦x<20}
のように表します。
一見すると暗号のようですが、いっていることは単純です。
『Pは要素xの集合で、xは3m(mは自然数)=3の倍数で、かつ、1以上20未満』という意味です。
最初は難しそうに感じるかもしれませんが、すぐになれるので安心してください。
集合と集合の関係
次に移ります。先ほどは要素と集合の関係を紹介しましたが、
今度は集合と集合の関係について考えます。
新たに、1以上20未満の4の倍数の集合Qを考えます。
Q={x|x=4n(nは自然数),1≦x <20}
この表記にはもう慣れたでしょうか?一応書き出しておくと、Q={4,8,12,16}となります。
ここで、集合PにもQにも属している要素があります。「12」がそうですね。
これは、先ほどの∈を使って、「12∈P」、「12∈Q」と書くことができます。この12の事を「集合Pと集合Qの共通部分」と言います。
ベン図で表すと、<ベン図1>の重なっている部分です。
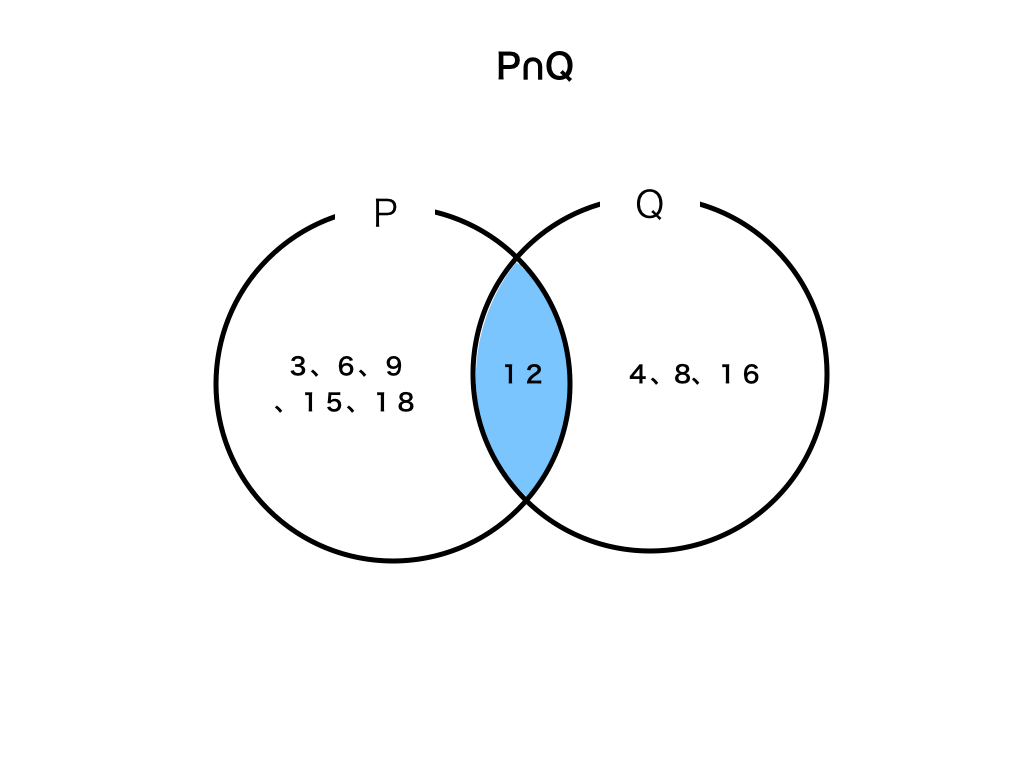
<ベン図1>
記号で書くと、P∩Q={12}となります。
<参考記事:「余事象とド・モルガンの法則を学ぶ」>
部分集合と集合の包含関係
更に1以上20未満の自然数の集合をSとおくと、<ベン図2>のように、集合P、集合Qを含んでいます。
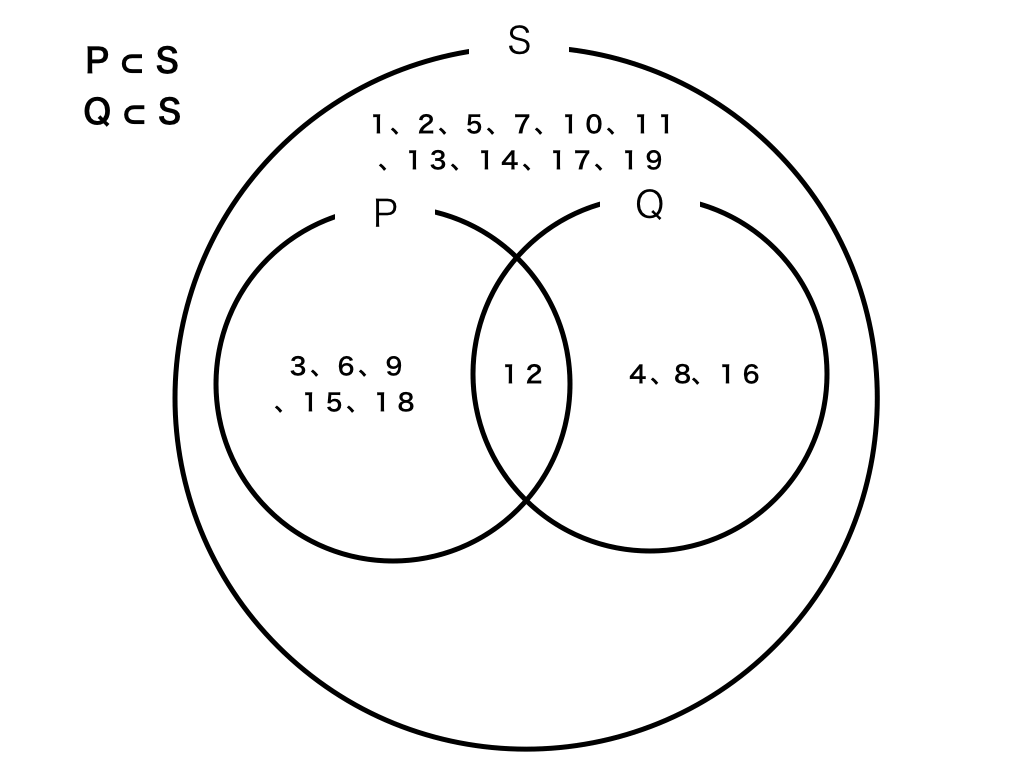
<ベン図2>
このような時「集合Pは集合Sの部分集合」、および、「集合Qは集合Sの部分集合」という言い方をし、要素と集合の時のように記号で表します。
集合と集合の場合は∈ではなく⊂の記号を使って、
P⊂Z、Q⊂Zと書きます。
写像とは
次に、二つの集合の対応関係について考える「写像」を解説して行きます。
写像とは、ある集合の要素から、他の集合の要素とを対応させること、と言えます。(??となると思うので、以下のイラストを見てください)
冒頭でも述べましたが、極めて重要な考え方です。抽象的で少し難しく感じるかもしれませんが、とりあえず目を通してみてください。
単射と全射・全単射
今<図3>の様な二つの集合P、Qがあるとします。
この集合の要素を詳しく見ていきます。なるべく理解しやすいように、例を使って解説していきます。
集合Pはあるクラスの生徒を要素とし、集合Qは身長を要素とするものとします。
全単射
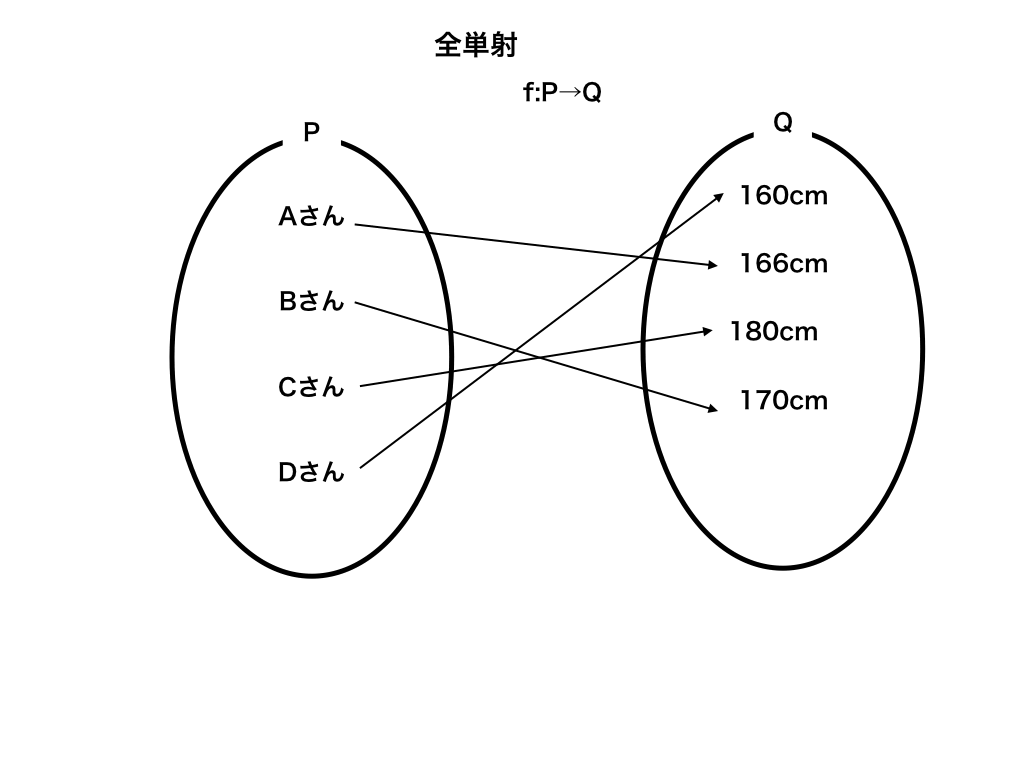
全単射とは、上の図のように2つの集合の要素が一対一に対応しているものをいいます。
Cさんの身長は180cm、これを$$f:C\mapsto{180cm} $$のように表します。
逆に、$$180cm \mapsto{C} $$も成り立ちます。
$$P\overset{f}{\underset{g}{\leftrightarrow}} Q$$
が成り立つとき、「全単射」と言います。
全射
今度は、「全射」と「単射」をみてみましょう。
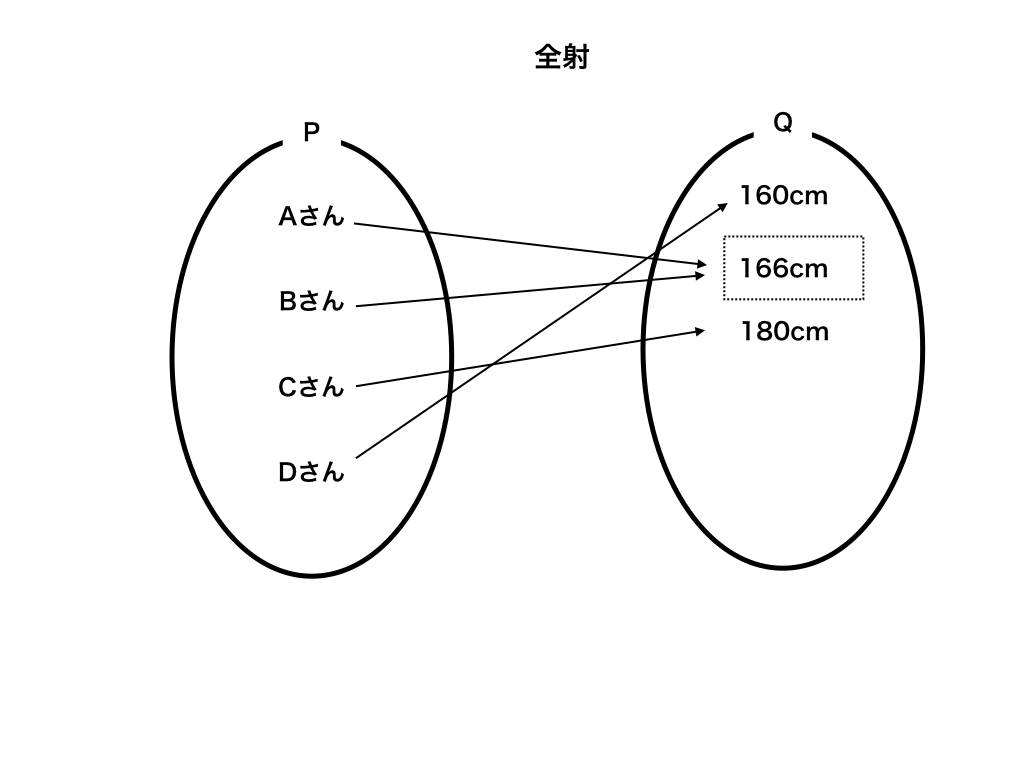
全射は、Pの要素を一つ定めると対応するQが見つかります。
しかし、全単射と違ってQの要素を一つ定めても、必ずしもPの要素が一つに決まりません。
(Qの要素166cmの人はAさんとBさんがいます。)
この様にP→Qの変換が可能でも、Q→Pの変換が不可能な時があります。
つまり、PからQへの写像は成り立ちますが、QからPへの写像(これを逆写像と言います)は成立しません。この様な時「全射」と言います。
単射
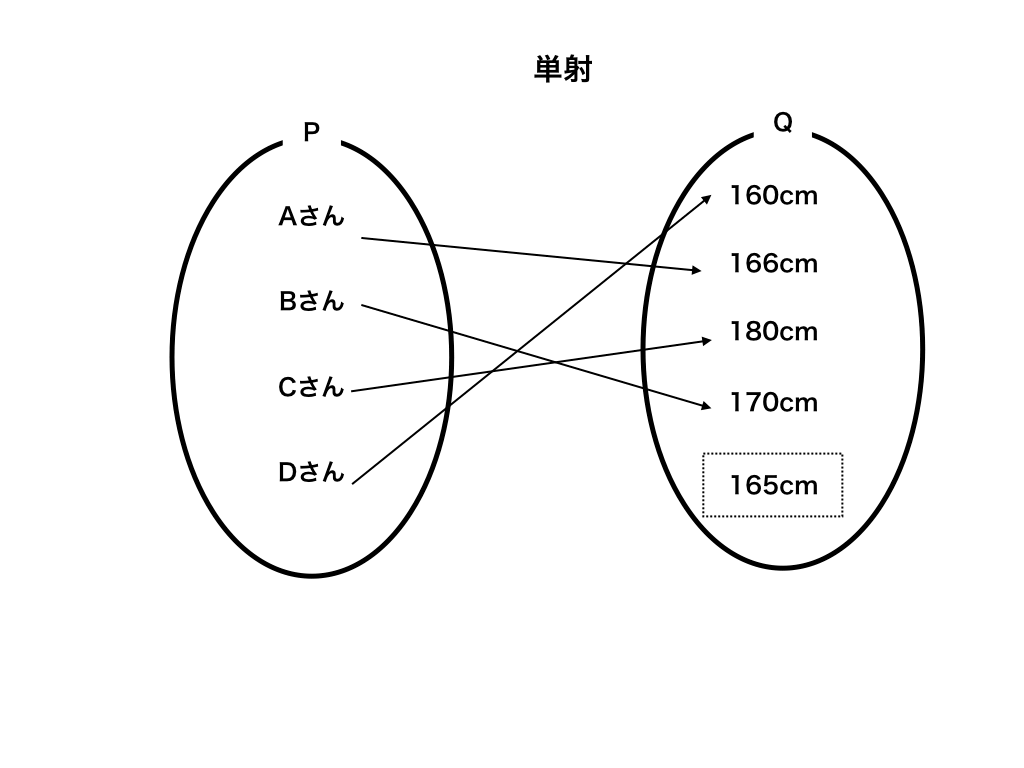
次は「単射」について。
P→Qはこれまで同様要素が対応していますが、
Q→Pを考えた時に四角で囲ったQの要素165cmに対応するPの要素がありません。
したがって、前者の時と同様にこの場合もQ→Pの変換はできません。
写像と線形代数(行列)へ
ここまでで、
・集合と要素の言葉の意味、表記法
・写像の初歩的な考え方
について学んできました。
これだけでは「写像」が何の役に立つのかよく分からないかもしれないので、
実際の例として、以下に線形代数の入門記事を紹介しておきます。
写像とベクトル・行列
誤解を恐れずに言うと、写像とは、要素と要素を対応させることであり、
要素の集合には、「ベクトル空間」も含まれます。
空間や平面は、「無数の点(位置ベクトルの先)の集合」であり(ベクトル空間)、これを移すことに行列が使われるのです。
写像の考え方は、特に線形写像を学ぶ際に、この記事を読んで何となくでも写像の意味を捉えているのと、いないのとでは大きく差が出てくるはずです!
(*詳しくは以下の記事、及び参考書等と共に学んでみて下さい!)
>>↓線形代数について詳しく学ぶ↓<<
>>「【随時更新】線形代数シリーズ:0から学べる記事総まとめ【保存版】」を読む<<
「線形代数第四回:一次変換とは何か。線形変換と行列による写像」
論理と集合の関連記事一覧
ここでは、高校数学1の『論理と集合』やその周辺分野の記事を紹介しておきます。
「背理法とは?証明の仕方と応用問題『tan1°は有理数か?』」
今回も最後までご覧いただき本当に有難うございました。
このサイトは皆さんのご意見や、記事のリクエスト、SNSでの反応などをもとに日々改善、記事の追加及び更新を行なっています。
・記事リクエストと質問・ご意見はコメント欄にお寄せください。
・また、多くの学生・受験生に利用して頂くためにSNSでシェア(拡散)&当サイト公式Twitterのフォローをして頂くと助かります!
・より良いサイト運営・記事作成の為に是非ご協力下さい。
・その他のお問い合わせ/ご依頼等はお問い合わせページよりお願い致します。

