
必要条件と十分条件・必要十分条件の見分け方で悩んでいませんか?
必要条件・十分条件・必要十分条件についてはどう判定して良いか分からなかったり、
方法を覚えても、テスト中にどっちがどっちか忘れてしまうなど、得意な人はあまり多くありません。
更に、入試では主にセンター試験で出題されるのみなので、良くわからないまま通り過ぎられることが多い分野です。
しかし実際には、必要十分条件の知識を背景とした問題が難関大を中心に多く出題されているのです。
そこで、この記事では、必要条件・十分条件・必要十分条件の“意味”と【判別する方法】、更にそれを忘れない“コツ”を解説していきます。
目次(タップした所へ飛びます)
必要条件と十分条件の意味と違い
本題に入ります。
その対策として、以下に紹介する方法を身につけてもらいます。
必要・十分条件を極端な例で理解する
必要/十分条件攻略への第一歩は、なんでも良いのですが極端な例を使って、その意味するところを理解することです。
ここでは、「生き物である⇄A君である」という命題を使っていきます。
包含関係と条件
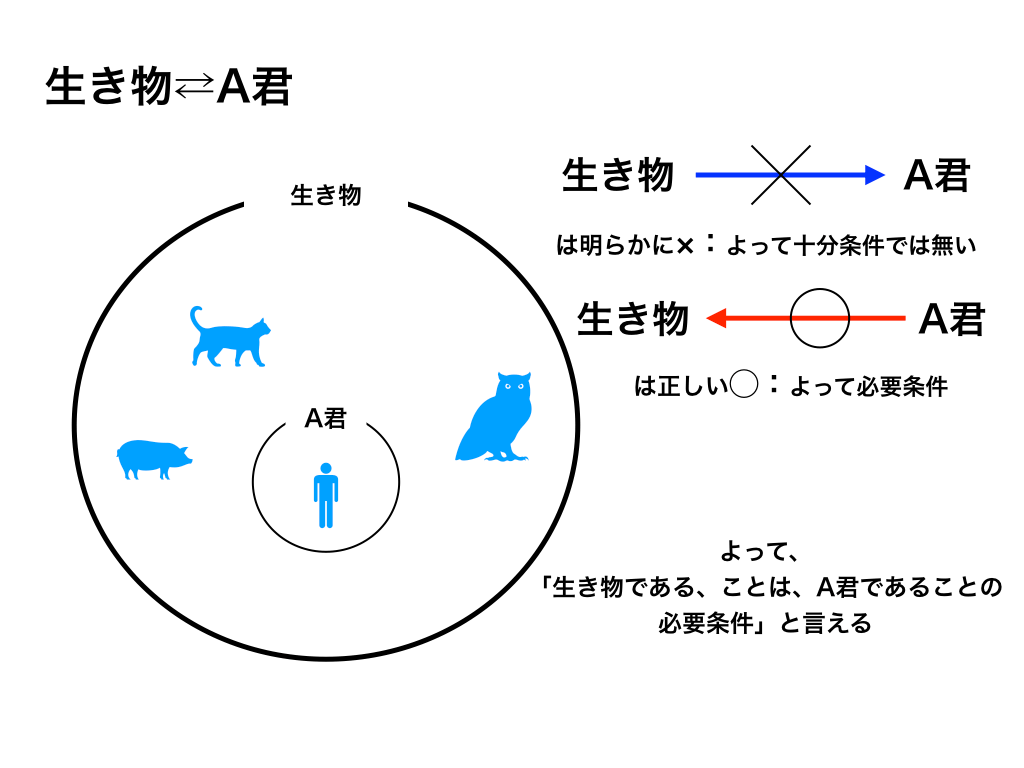
<上図の例>の様に、
生き物、ならば、A君である。はあきらかに偽ですが、A君、ならば、生き物である。は正しいです(真)
※上の様に、包含関係を図にする事でもっと難しい問題でも対応しやすくなります。
これを論理と集合的に表すと、(生き物)→(A君)が偽、(生き物)←(A君)は真となります。
この様な時、左側の(生き物)を主語*にして、「生き物であることは、A君であることの『必要条件』である」と言います。
必要条件と十分条件・必要十分条件の見分け方のコツ
一番多い悩みがこの『必要/十分/必要十分条件の見分け方』です。
必要条件なのか十分条件なのか、わからなくなってしまうという事が非常に多いです。
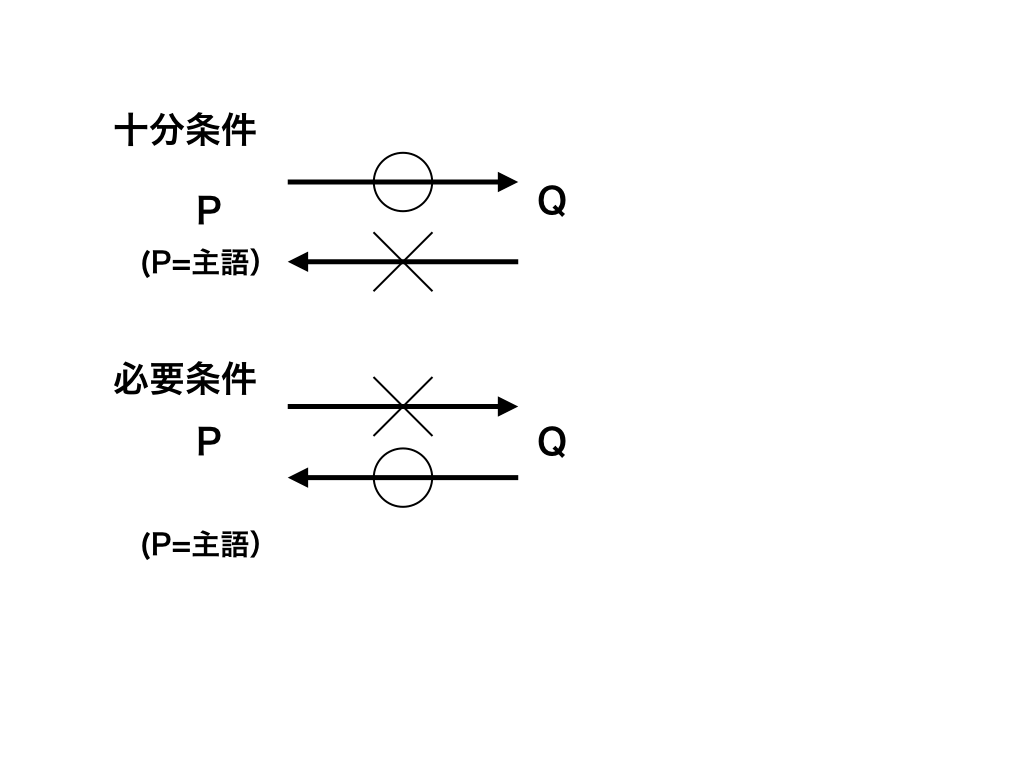
←と→が両方とも真なら『必要十分条件である』、両方とも偽なら『必要条件でも十分条件でもない』と答えれば良いのですが、、
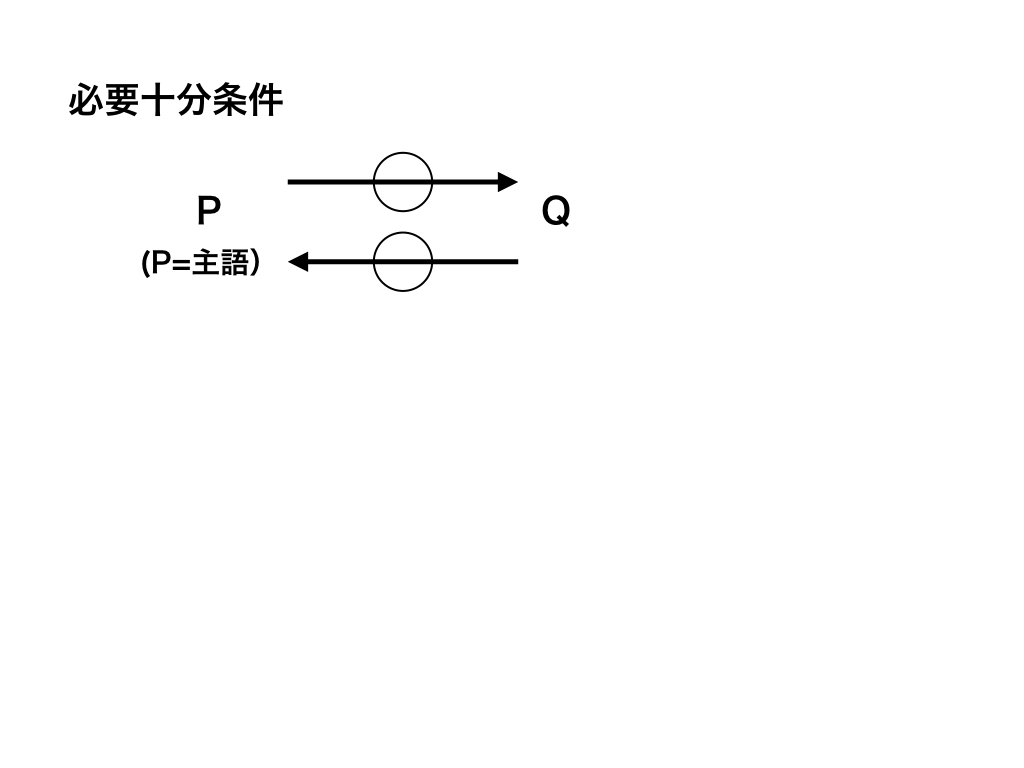
見分け方の攻略法:十⇄要
そこで、有効なテクニックとして、【十⇄要】を紹介します。
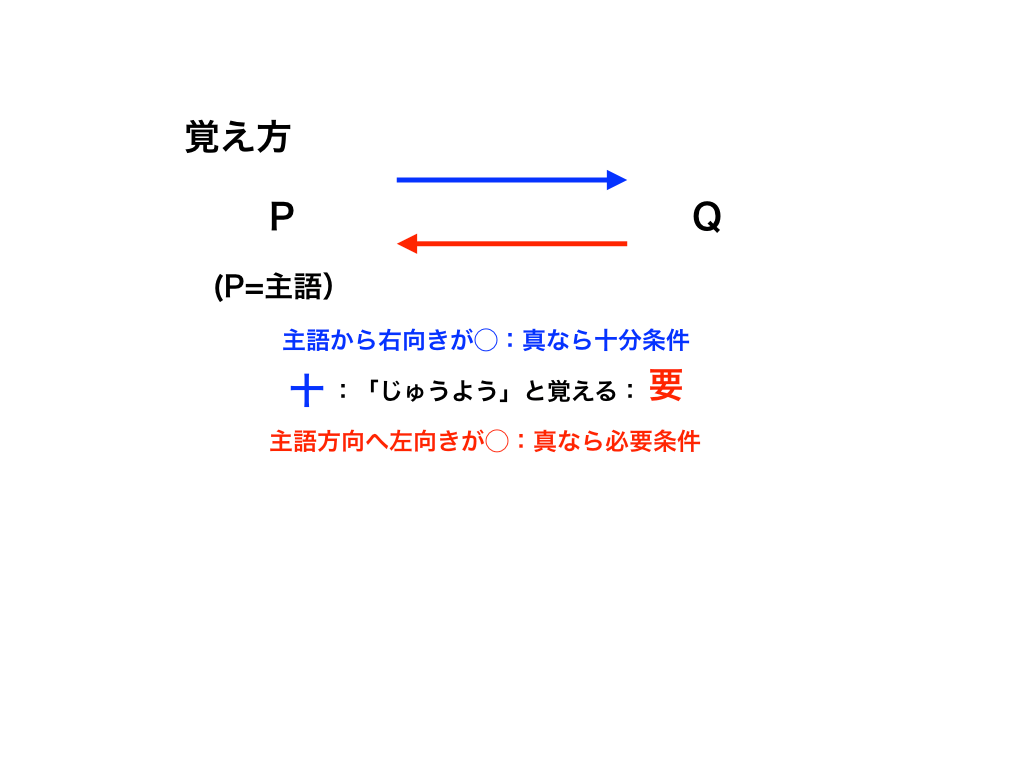
上のイラストの通り、P:主語を左に持ってきて(先ほどの例では生き物)、Q(先ほどの例ではA君)を右にします。
・P→Qが真ならば、PであることはQであることの十分条件。
・P←Qが真ならば、PであることはQであることの必要条件と言えます。
覚え方は、”重要”とかけて『十⇄要』をイラストの様にP,Qの下に書いておきます。
次の例題でこの十⇄要の使い方を具体的に解説していきます。
(*):この記事中での「主語」は、論理学での主語と少々意味合いが異なります。高校数学での理解のし易さを優先している事をご了承下さい。
十⇄要の使い方(見分け方)定着問題
では、実際にどの様な問題を解くのか、また上で紹介した解法を今記憶して定着させるために、例題を数問解いていきましょう。
「十⇄要」と「主語、真と偽」に注意してください。
次の「」の中に、「必要条件である」「十分条件である」「必要十分条件である」「どちらでも無い」を入れよ。
(例題1):x>2である事は、\(x^{2}>4\)である事の「」
(例題2):xは無理数である事は、
\(\sqrt{28}\)が有理数である事の「」
(例2:センター改)
例題解説
(解説1)まず、この例題1では「x>2」が主語になっているので、この下に「十」と書いて、
\(x^{2}>4の下に「要」と書きます。\)
次に、十⇄要の右向き、左向きの真偽を考えます。
x>2であれば、必ずその二乗は4より大きくなりますから、右向きは真です、
次に、十←要を考えます。
\(x^{2}>4\)は、x>2で無くとも、例えばx=−3でも成立します。
つまりx<−2でも成り立つのでこれは偽です。
(この様な、「偽」の例を「反例」と言いマーク式では無い記述問題では、反例を書く必要があります。)
さて、この結果と十⇄要を比べると、十→要が◯、十←要が×なので、
\(x>2はx^{2}>4である事の「十分条件である」\)
が答えとなります。
(※まだ慣れていない方は、先ほどのイラストを参照してください)
(解説2)手順は例1と同様です。
\(x=無理数と、 \sqrt{28}x=有理数、\)
のそれぞれの下に十⇄要を書いて、→と←の真偽を調べます。
ここで、十→要は、例えば
\(x=\sqrt{5}の時\sqrt{140}=無理数(反例)となって偽。\)
たった1つでも反例があれば、偽
次に、十←要はx=0の時も成り立ってしまう(反例)ので「偽」(※たった1つでも、反例があれば偽になります)。
従って、十⇄要の”→”も”←”も”偽”のために答えは「必要条件でも十分条件でもない」が正解となります。
論理と集合・証明関連記事
コツは少しつかめてきたでしょうか?
この必要・十分・必要十分の判断を訓練するには、センター数学1Aの過去問が最適なので、ぜひ短時間で全問正解出来るように繰り返しといてみて下さい。
「真」である事の証明法一覧
記述対策としては、真であることを証明する必要があるので、その証明法は以下の「対偶法」、「背理法」、「数学的帰納法」の記事をそれぞれご覧ください。
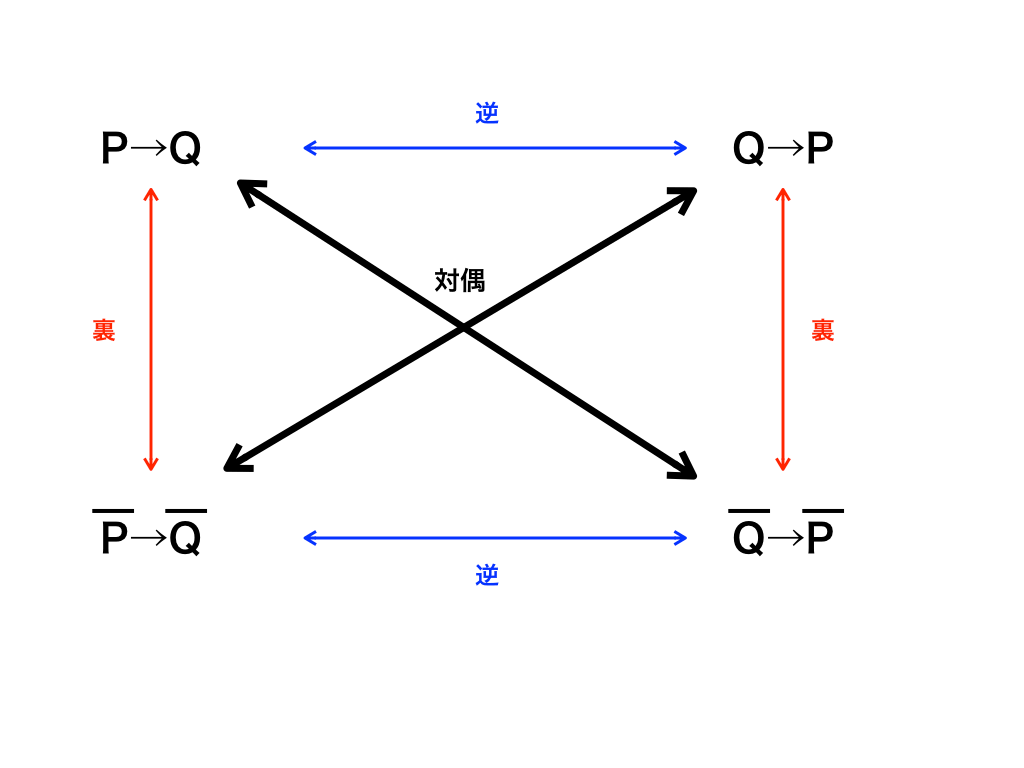
※逆・裏・対偶および対偶法については、「対偶法とは?そして逆・裏・対偶の意味と証明の仕方」の記事で詳しく解説しています。ぜひご覧下さい!
※背理法については、「背理法とは?証明の方法と例題、そして『tan1°は有理数か』」
※数学的帰納法は、「数学的帰納法の意味と証明のコツ」
今回も最後までご覧いただき、本当に有難うございました。
この記事がお役に立ちましたら、シェア&当サイト公式Twitterのフォローをお願いします!
このサイトは皆さんの貴重なご意見や、記事のリクエスト、SNS上での反応などをもとに日々改善・記事の追加・更新を行なっています。
そこで
・記事のリクエストと質問・ご意見はコメント欄にお寄せください。
・その他のお問い合わせ/ご依頼などはお問い合わせページよりお願い致します。
・より良いサイト運営・記事作成の為に是非ご協力お願い致します!

