
〜加法定理の証明と東大からのメッセージ〜
(NEW):「加法定理を使う証明問題の解説記事へ」を追加しました。
目次(タップした所へ飛びます)
三角関数において最重要な加法定理
三角関数の公式で覚えておくのは1種類だけ!公式暗記から導き方へ〜でも書きましたが、
少なくとも高校範囲の三角関数公式はぼ全て加法定理から導けるので、暗記の必要はありません(もっとも何度も使っているうちに自然と覚えてしまいますが、、)
具体的に加法定理からは、
二倍角の公式、三倍角の公式、半角公式、<→「2倍/3倍/半角の公式を覚えず導く!」>
和積・積和の公式<→「和積・積和の公式の作り方」>
三角関数のsin型、cos型の合成、<→「三角関数と加法定理は真逆の関係:cos型で合成できますか?」>
などなど・・・本当に全て導けてしまいます。
三角関数は高校数学で“最重要の関数”です。
文系でセンターのみ使う人も、理系で数3まで必要な人も必須です。
だからこそ、あいまいな公式暗記や語呂合わせといったことに時間を取られず、本質的な”覚えず導く”という方法を習得することによって、周囲に大きく差をつけることができるのです!
では、加法定理そのものは(当然証明出来るようにした上で)暗記すべきなのでしょうか?
結論から言うと暗記しておくべき、と考えます。(話が長くなってしまったので、理由は記事の最後にまとめました)
では、その元々の加法定理はどうやって導くのでしょうか?
難関大はこのような基本中の基本を聞いてきます。
むしろ大学のレベルが上がるにつれて、公式の証明問題や普段使っている定義の証明or評価を聞いてくる傾向が強いです。
実際に加法定理の証明をせよ、という問題が東京大学1999年前期で出題されています!
また最近では、lim(x→0)sinx/x=1 の証明問題が阪大で出題されました。
普段何気なく使っているうちに、それを使って難問ができるようになったと思っても
本当に基礎を理解して使っているのか?上辺だけの解法暗記ではないか?
と問われるのです。
加法定理を証明していきましょう【本題】
もちろん何通りも証明方法はありますが、最も一般的な証明を載せます。
使用する定理や公式
使うのは単位円、距離の公式、余弦定理そして還元公式です。
還元公式については「2stepで攻略暗記不要の還元公式まとめ」で纏めているのであやふやな人はチェックしておいて下さい。
証明の手順
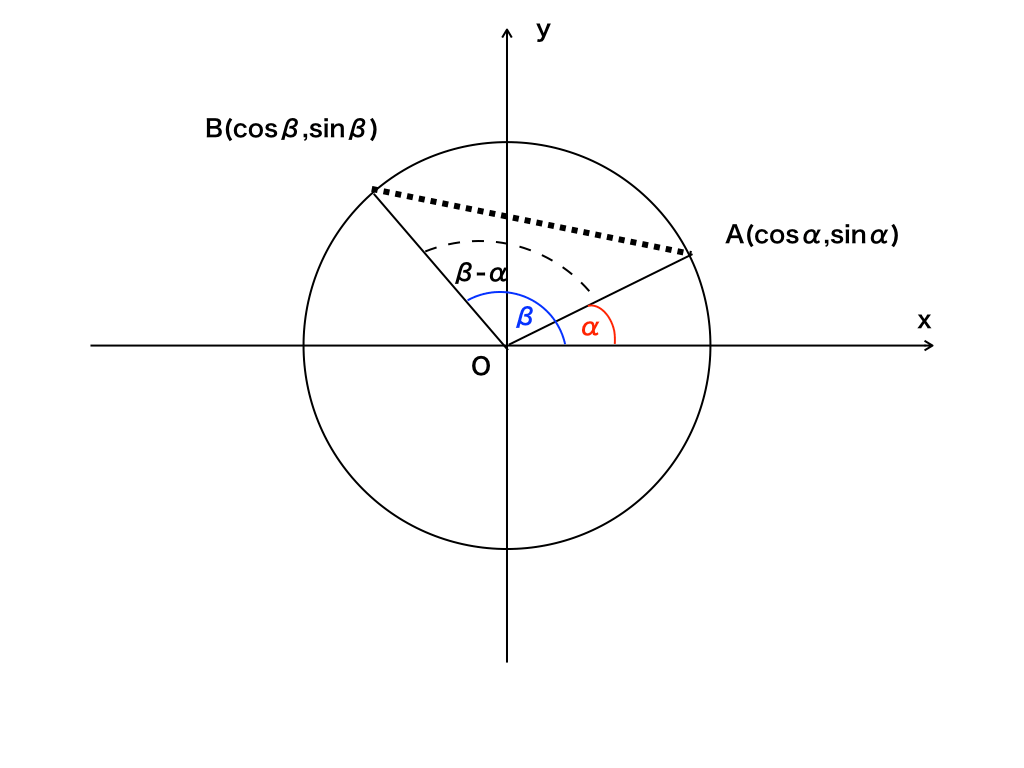
手順は<図1と以下>の通りです
座標平面上に単位円を置き、単位円上の2点:AとBの座標をcosとsinで表わします。
次に、その2点間の距離を三平方の定理を使って求めます。・・・(1)
同時にA,Bは単位円上にあることから、二辺が半径1であることより、三角形ABOに余弦定理(余弦定理については「三角比の表と正弦・余弦定理」を参照してください)を用いて2点間の距離を求めます。・・・(2)
(1)と(2)の二つの式の値(=距離)の値は同じですから、(1)と(2)を=で結んで整理すれば加法定理のうちの一つが証明できます。
具体的に計算(証明)していきます。(※最後に等式で結ぶので、距離の二乗のまま計算を進めます)
三平方の定理の利用
(1):三平方の定理より、AB2=(cosβ-cosα)2+(sinα-sinβ)2
これを展開して、
=cos2β+cos2α-2cosβcosα+sin2α+sin2β-2sinαsinβ
sin2θ+cos2θ=1 より、
=2-2(cosβcosα+sinβsinα)・・・(1')
余弦定理の利用
(2):次に、余弦定理を使って、
AB2=OA2+OB2-2・1・1×cos(β-α)
OA=OB=1 (∵単位円の半径)
AB2=2-2cos(β-α)・・・ (2')
(1')=(2')なので、
2-2(cosβcosα+sinβsinα)=2-2cos(β-α)
よって、cos(β-α)=cosβcosα+sinβsinα
・・・これでcos(β-α)型の加法定理を導くことができました。
cos型からsin型・tan型への変形
次に図1で示したcos(β-α)をcos(β+α)型とsin型に変形します。
ここでは還元公式<参考:「sin(θ±π/2)など18種類以上ある還元公式の暗記量を激減させる方法」>の考え方を利用します。
つまり、(βーα)のαを(ーα)や、{π/2ー(β+α)} 等に変えて計算します<図2>参照

<図2:還元公式で他の形の加法定理を導く>
最後にtan型の加法定理は、三角比・三角関数の相互関係(sin/cos)=tanより導出します。
いかがでしたか?
いずれも教科書に載っているレベルですが、実際の入試、それも東大数学で問われた時戸惑った受験生は多かったのです。
更にこれが“大問1”であったので、ここで焦ってしまった受験生は残りの大問に尾を引き、結果合否に影響したことは想像に難くありません。
毎年、東大で出題される問題は他の大学や高校、塾など幅広くに示唆を与える(=メッセージ)事が多いです。
非常に教育的な良問が揃っています。
難関大を目指している人こそ諸公式は全て証明できる様にしておいて下さい。
「教科書だけで東大に合格した」という人がたまにいますが、あながち嘘では無いでしょう。
教科書を深く考察する事で、本質が理解しやすくなり、あとは過去問のみやればある程度のセンスがあれば可能と思われます。
ただ一般的には「センス」の代わりに参考書や問題集を挟みますが。タイトルの教科書だけで〜のイミが伝わったでしょうか。
成績が良い人ほど、早くからこの意味を理解しています。
加法定理を使う証明問題へ進む
東大と並ぶ、最難関大学である「京大」で出題された、超良問『tan1°は有理数か。』を今回示した加法定理と背理法を用いて証明する方法を解説した記事を作成しました!
三角関数の公式の導き方・自然に覚えてしまう方法一覧は、以下の記事よりご覧下さい。
加法定理を利用して三角関数の公式を自然に覚える!総まとめページ
加法定理は暗記すべきか?
(※先ほどの加法定理と暗記についての続きです)
これは様々な意見があると思います。
「毎回単位円を使って加法定理を作る→そこから変形して他の公式を導出」という流れが教育的には望ましいです。
が、時間制限がある入試や模試では少し効率的ではないでしょう。
そこで筆者としては、時間制限のない普段の学習では加法定理を作る所から始めて、
→それを繰り返して頭の中で加法定理を作れるくらいにspeed upすれば、加法定理のみ、覚えてしまっても良いと考えます。

