
希薄溶液の凝固と冷却曲線
冷却曲線の図を見ると、冷却時間とともに温度が下がる様な【単純なものではない】事が分かります。
それぞれの「変な」動きには当然理由があるのですが、きちんと答えられるでしょうか?
冷却曲線は、『しっかりと溶液分野を理解しているのか?』をはかる事ができるので、よく出題される分野です。=差を付けるチャンスでもあります。しっかりと理屈を抑えて、得点源へ変えていきましょう。
※この記事は「蒸気圧降下と沸点上昇/凝固点降下の関係と仕組みが分かる」の続編です。
未読の方は先に読んでおくと理解が進むかと思います。
目次(タップした所へ飛びます)
冷却曲線とは?
液体の温度を下げていくと当然凝固が始まります。<「物質の三態:状態図と飽和蒸気圧曲線の見方」参照>
ここで、純溶媒(溶質が溶けていない液体)と希薄溶液(純溶媒に不揮発性の溶質を加えた溶液で、その濃度が低いもの)
を冷却していくと、同じ時間冷却していても温度変化の仕方が変わってきます。
それを図にしたものが<図一>の様な温度ー時間グラフで「冷却曲線」と呼びます。
今からこの違いの理由を解説して行きます。
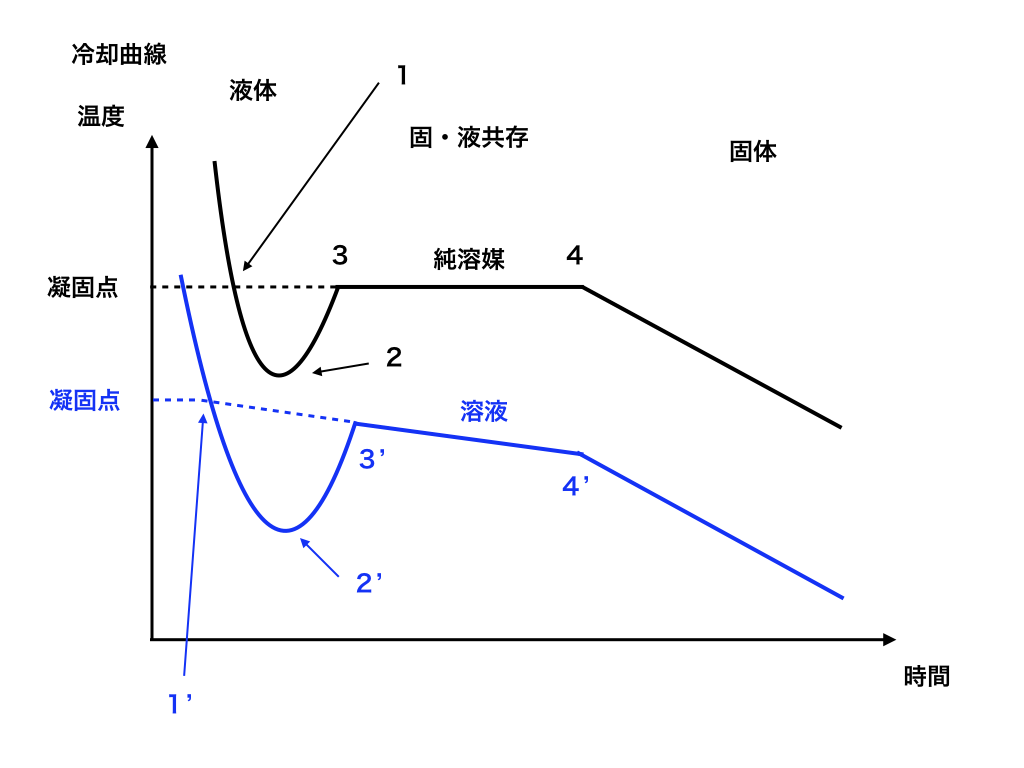
<図一:冷却曲線>
凝固点はどこか(何度か?)
溶媒や溶液が凝固する温度は、純溶媒の場合(1)で、溶液の場合は(3‘)、(4’)の傾きを伸ばした所にある(1‘)です。これを「外挿」すると言います。
この(1)と(1’)の差が、前回解説した、いわゆる「凝固点降下度」です。
簡単におさらいしておくと、溶媒分子から先に凍っていくので、
純溶媒だけに比べて、溶質を含む溶液は融解する分子数=凝固しようとする分子数、
となるための温度が下がる事を言いました。
※「蒸気圧降下と希薄溶液の沸点上昇と凝固点降下の仕組み」の記事に仕組みを詳細に説明しているので、
沸点上昇や凝固点降下の仕組みをすぐに説明できない人は是非ご覧下さい。オススメです!
過冷却とは
純溶媒と溶液のグラフを見ると、両方とも一度大きく温度が下がった後一旦温度が上昇します。
この冷却曲線では、凝固点は(1)と(1’)の場所です。しかし実際に凝固が始まるのは(2)、(2‘)です。
つまり、凝固点である(1)、(1‘)より温度が低いにもかかわらず、液体は(2)、(2’)まで凍りません。
この様に、凝固点以下でも液体のままである状態の事を過冷却と言います。
グラフが一旦上昇する理由
その後温度が(3)、(3’)まで上昇する理由は、凝固する事で凝固熱が発生し、
その凝固熱の方が冷却される事で外部から奪われる熱より大きい為です。
この理由は入試でも頻繁に問われます。
純溶媒と溶液で凝固中のグラフの傾きが違う理由
更にその後、純溶媒はすべて凝固するまでその温度は変化しませんが、
希薄溶液の方は凝固しながら温度が下がっていきます。
その理由は、純粋な溶媒は一部が凝固しても、溶質がないので質量モル濃度は0で変化せず、結果的に凝固点降下が起こりません。
しかし、溶質が溶けている溶液は溶媒が凝固して行くに従って溶質の質量モル濃度が大きくなります。
すると、凝固点降下度が大きくなり、
元々の凝固点よりも低い温度でないと凝固しなくなる為、右肩下がりにグラフが傾きます。
少し長いですが、ここも入試頻出&理解しておく必要があるので、頭に入れておきましょう。
最終的に(4)、(4‘)で純溶媒・溶液共に完全に凝固し、あとは固体(氷)の温度が下がっていきます。
これが、溶液と純溶媒の凝固の流れです。
最後に水和物の計算処理の方法を解説しておきます。そして、今回の復習問題を解いて知識を整理しておきましょう。
水和物の質量モル濃度への変換
ここまで読んで頂いているので、冷却曲線の記述問題は大抵解ける様になっているはずです。
残っている頻出問題は、冷却曲線に関連して出題される「凝固点降下度」の計算問題です。
基本的な凝固点降下度の問題は、前回解説しているので
<参考:「蒸気圧降下と沸点上昇/凝固点降下」>
今回解説するのは、水和物の凝固点降下度を求める問題です。
水和物は嫌いな人が多いですが、以下の手順に従って着実に計算すれば、
じつは別に特別難しいわけではない事が分かってもらえるはずです。
問題:塩化カルシウム・二水和物【\(CaCl_{2}\cdot 2H_{2}O\)】14.7gを、溶媒である水\(H_{2}O\) 100gに溶かした時の凝固点降下度を求めよ。
ただし、塩化カルシウムの電離度α=1、
水の凝固点降下は\(1.85(\frac{K\cdot Kg}{mol})\)
各原子量を、Ca:40, Cl:35.5, H:1 ,O:16とする。
水和物の凝固点降下度の例題の解答解説
必要なものは質量モル濃度\((\frac{溶質のmol}{溶媒の質量Kg}\)なので、
手順(一):\(CaCl_{2}\cdot 2H_{2}O\)全体(塩化カルシウム・二水和物)に占める、\(H_{2}O\)の質量を求めます。
$$14.7\times \frac{18\times 2}{147}=3.6$$
より、3.6gが水の質量です。
手順(二):塩化カルシウムのmol数と水(溶媒)の質量を計算します。
塩化カルシウムのmol数は
$$\frac{14.7-3.6}{147}=0.1 より、0.1(mol)$$
水の質量は、100+3.6=103.6(g)
手順(三):(二)の式では\((\frac{mol}{g})\)なので、凝固点降下の式が使える様にする為に\((\frac{mol}{Kg})\)へ変換します。
$$\frac{0.1(mol)}{103.6(g)}を\frac{x(mol)}{1(Kg)}に変換する$$
(分かりにくい時は比で考えても良い)
\(103.6:1000=0.1:x\)
\(よって、x≒9.69× 10^{-1} (mol/Kg)\)
手順(四):(三)で求めた質量モル濃度× 水の凝固点降下
\(を計算すれば、CaCl_{2}\cdot 2H_{2}Oを溶かした\)
溶液の凝固点降下度が求まります。
\(9.69× 10^{-1}(mol/Kg)\times 1.85(\frac{K\cdot Kg}{mol})=1.792...\)
より、この水和物の凝固点降下度は、
有効数字二桁で1.8(K)・・・(答)
となります。
冷却曲線まとめと溶液シリーズ一覧
・まずは凝固点の意味と凝固点降下のメカニズムをしっかり復習しましょう。
・冷却曲線の純溶媒と溶液の温度ー時間グラフは、今回の内容がそのまま問題になるくらい重要なので、
しっかりと一つ一つの現象の「意味/理由」を答えられるように何回か復習しておいて下さい。
・冷却曲線のメインで出てくる【凝固点降下の計算問題】は、
水和物を持っていたり・電離度αが=1ではないなど、少しひねられたものが多いので、問題集などで応用的なものに触れて解法を習得しましょう。
溶液シリーズ一覧
第一回:「浸透圧とファントホッフの式をわかりやすく解説」
第二回:「状態図の見方と飽和蒸気圧曲線を読み取る応用問題」
第三回:「蒸気圧降下と沸点上昇/凝固点降下の関係と仕組みが分かる」
第四回:「今ここです」
(NEW!):「溶液・希薄溶液と気体分野の記事まとめ!」
今回も最後までご覧いただき有難うございました。
質問・記事について・誤植・その他のお問い合わせはコメント欄、又はお問い合わせページまでお願い致します!
お役に立ちましたら、シェア&当サイト公式Twitterのフォローをお願いします!

