媒介変数表示された曲線のグラフと増減表/面積の求め方を解説

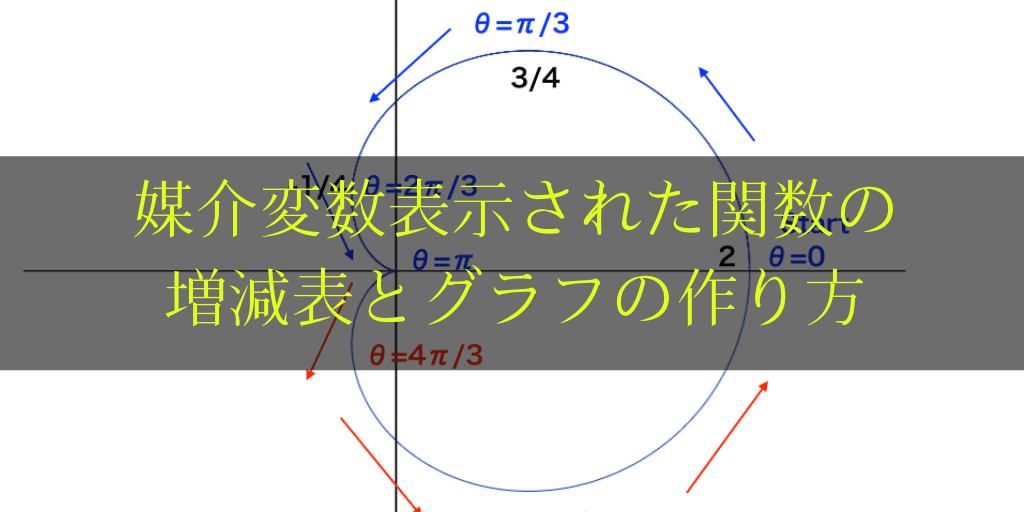
パラメーター表示された曲線のグラフと面積

＜この記事の対象者＞：数三を学習していて、媒介変数（パラメーター）表示された曲線の描き方・増減表の作り方などがわかりづらい・苦手な人。

＜内容＞：基本的な『dx/dt』の計算の仕方などから解説し、『２つの媒介変数の式から→増減表の作成→”x-y”座標平面に曲線を描き→その面積を求める』レベルまで、イラストを豊富に用いながら解説します。

関連記事:「数学Ⅲの微積分とその応用まとめ」/「媒介変数と軌跡(図形と方程式)」

媒介変数(パラメーター)とは？

例えば、馴染み深い：\(y=x^{2}\)を”t”で表してみると、\(x=t、y=t^{2}\)のように、x、yそれぞれをtという媒介(間に入って2つをつなげる)変数（パラメーターとも言います）の式で表すことができます。

試しに、上の”x=tをy=t²”に代入すると”y=x²”と言う二次関数に戻ります。

実際に出題される【媒介変数表示された曲線】はもっと複雑で、簡単に代入してy＝のカタチにすることが難しいことが多いです。

そのため、媒介変数表示された問題では、x,yを別々に微分するという、これまでとは少し違った方法をとります。

パラメーター表示された関数(曲線)の例

(例題1)：→この項で解説します。

\(x=\cos t\)

\(y=\cos 2t\)

ただし、０≦t≦2π

特別な増減表の作り方

この項では、＜例1＞を使って”媒介変数表示”された曲線の“増減表”の作り方を紹介します。

媒介変数(パラメタ)表示での増減表の作成法は、先ほども述べたように通常の場合と少し違います。

具体的には「y＝f(x)」の増減表を作る時に上から”x”・”dy/dx=f'(x)”・”y”とするのに対して、

「x＝(tの式)、y=(tの式)」の場合には、”t”、”dx/ dt ”、”dy/ dt”、”x”、”y”と埋めていきます。

（増減表の順番や作り方は参考書や教科書によって異なるので、一旦このやり方を理解したら、自分が作りやすい方法を選んでください。）

手順１：x＝,y=のそれぞれをパラメーターの文字tで微分する

x＝cos(t) をtで微分、つまり”dx/dt”を求めます、

見た目ほどややこしいことはなく、普段”x”で微分している”変数”の部分が”x”から”t”に置き換わっただけです。

costをtで微分すると、-sin(t)

y=cos²(t)をtで微分すると、合成関数の微分を使って＜参考：「合成関数の微分法の解説」＞、

dy/dt=2・cos(t)・-sin(t)

：（外側のcos²(t)の微分）×（cos(t)）の微分をしているだけです。

手順２：dx/dt=0の前後での符号を確認し、→/←を書き込む

次に、”dx/dt”が求まったので、符号の変化位置を確認します。

以下の増減表のように、”dx/dt”が”正”の時は増減表に右矢印（→：x軸正方向）を、

”dx/dt”が”負”の時は左矢印（←：x軸負方向）を書き込みます。

手順３：dy/dt=0の前後での符号を確認し、↑/↓を書き込む

同様に、”dy/dt”の時も、符号の変化位置を確認します。

以下の図のように、dy/dtが”正”の時は増減表に上矢印（↑：y軸正方向）を、

”dy/dt”が”負”の時は下矢印（↓：y軸負方向）を書き込みます。

まとめ：横向きの矢印と上下方向の矢印を合わせてグラフを作る

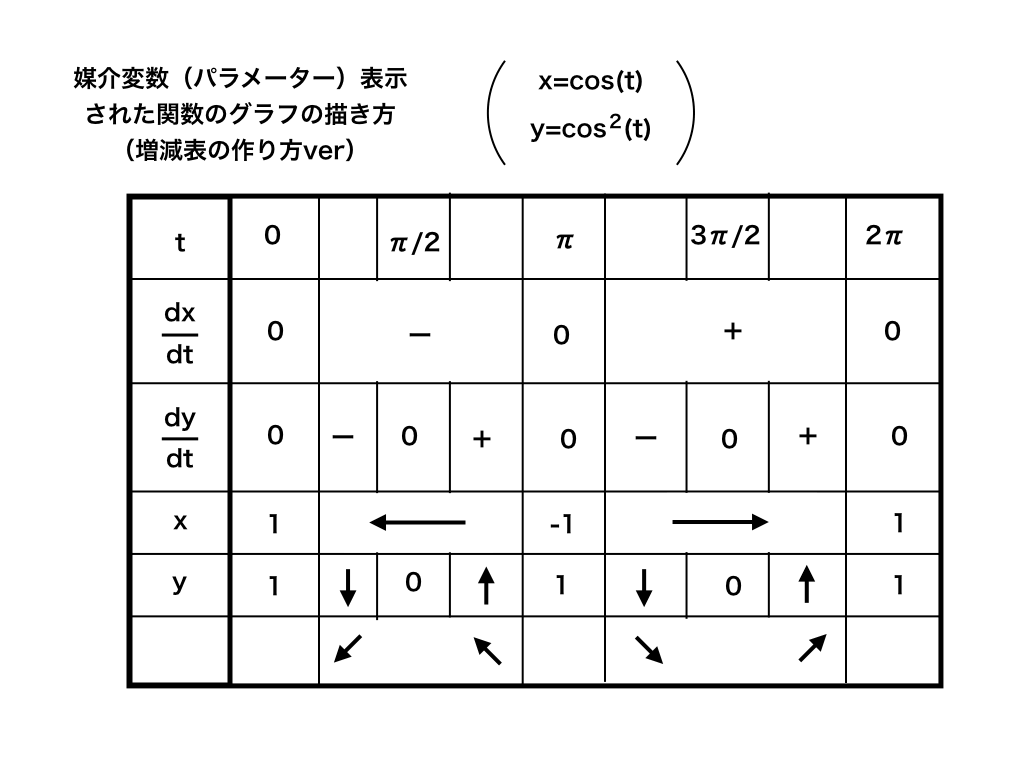
＜例題１の増減表の一例＞

グラフを描く

上で作った増減表１をもとにグラフを描いていきます。

一番下の欄をみると、tが0からπ/2に進むとグラフは(1,1)から(0,0)へ左下向きに、

tがπ/2からπに進むと(-1,1)へ左上向きに進むことが分かります。

同様に、

πから3π/2へは(0,0)へ右下へ、

3π/2から2πへは(1,1)へ右上に進みます。

これらをまとめて、t＝0からにt＝πまで（青矢印の順に）書き込み、そこから折り返してt＝2πまで赤矢印の通りにグラフを作成していきます。

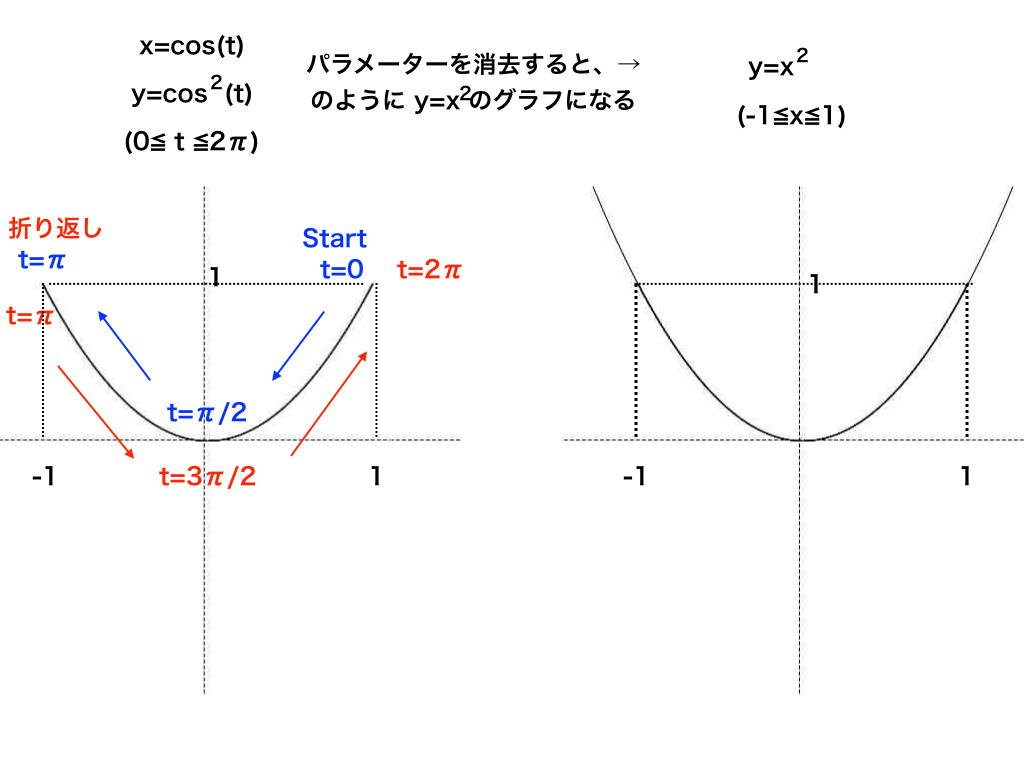
＜媒介変数のグラフ(例1)＞

作成したグラフを見ると、確かにパラメーターを消去したy=x²のグラフ（右）の（-1≦x≦1）の部分である事がわかります。

（左の）定義域の（0≦x=cos(t)≦2π）が、（右の）定義域の（-1≦x≦1）に対応しています。

媒介変数で表されたグラフと面積

ここまでで、ごく基本的な『媒介変数表示された曲線(関数)』のグラフの書き方・増減表の作り方を紹介しました。

ここからは、例題1の復習をしながら増減表(少し省略した、別のパターンを紹介します。）→グラフを描く→グラフによってできる面積を計算

の順番で解説していきます。

求積問題への応用と増減表：type2

応用問題２：以下のように表される

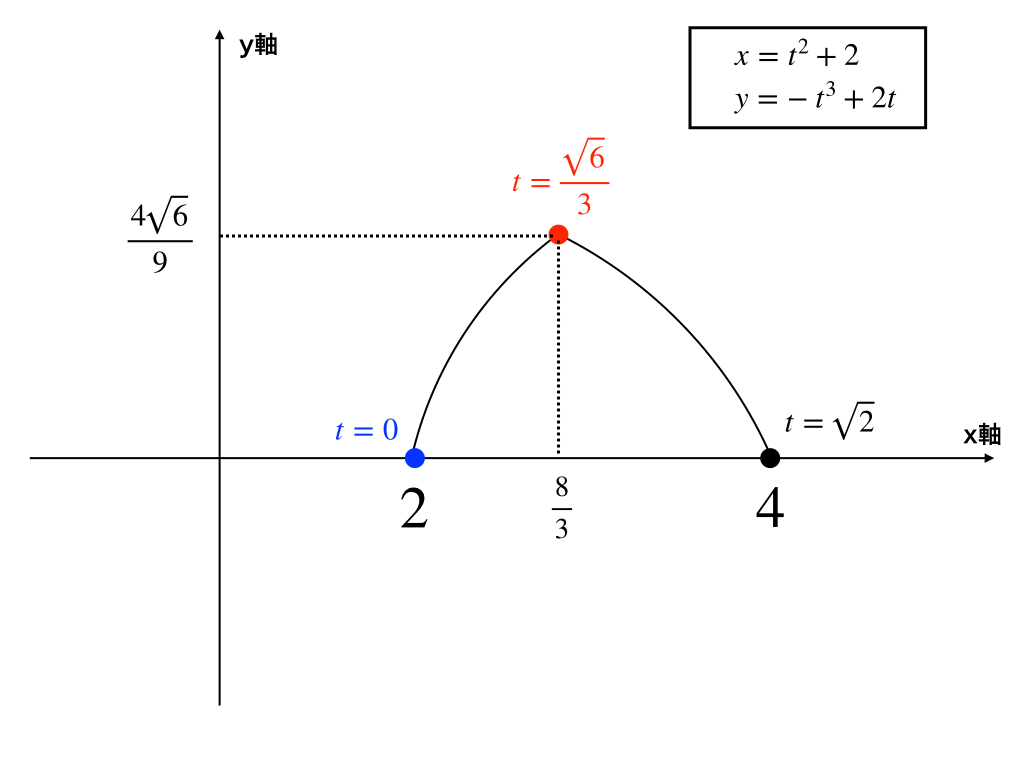
\(x=t^{2}+2\)

\(y=-t^{3}+2t\)

\(（0≦t≦\sqrt{2}）\)

↑曲線のグラフを描け。

また、曲線とx軸、y軸で囲まれた部分の面積(Sとする)を求めよ。

解説2：増減表type2の作成まで

これまで同様に、x・yのそれぞれをtで微分し、dx/dt,dy/dtをうめていきます。

はじめの問題では、かなり丁寧にうめていきましたが、慣れてくると以下の様に簡略化した【必要最低限】の増減表でグラフをかける様にしておきましょう！

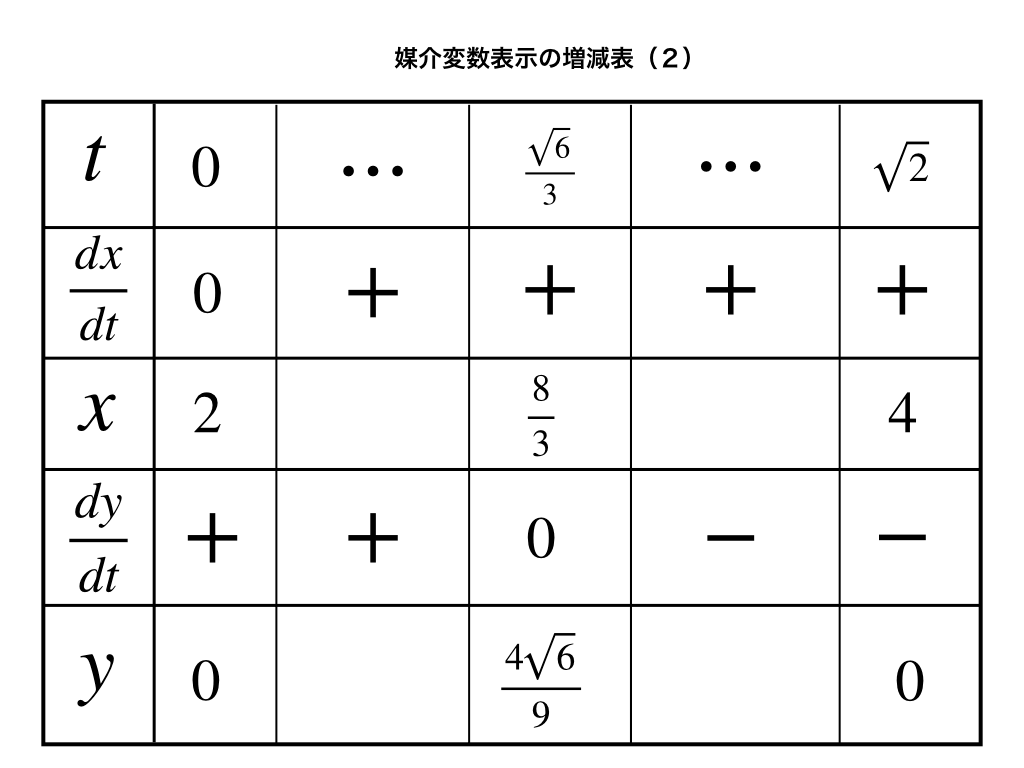
結果的に上↑のような増減表が作成できます。

解説2-2：グラフ作成と面積の求め方

次に、グラフは『tの流れに沿って』なめらかに線を引いていきます。

次は面積です。簡単に積分出来る形の関数ではないので、tのまま積分することを考えます。

つまり→「置換積分の復習・解説」の様に置換積分を利用して求積問題を解いていきます。

$$\int_{2}^{4}y dx =\int_{0}^{\sqrt{2}} y \frac{dx}{dt}dt$$

※：積分区間が変わるのでミスしない様に注意！

$$=\int_{0}^{\sqrt{2}} -2t^{4}+4t^{2} dt =\frac{16\sqrt{2}}{15}$$

$$結果的にS＝\frac{16\sqrt{2}}{15}$$

まとめと次回「弧長」へ

・類題をこなして、入試・数検等で頻出の”有名曲線”を描く練習をしておきましょう。

・次回は、この記事の“媒介変数表示された”曲線の長さ(弧長)・求積(体積version)などさらに応用した分野について解説していきます。(作成中)

関連記事まとめ・続編へ

＞＞「数学Ⅲ：微分法・積分法とどの応用記事まとめ」＜＜

次回：「（作成中）パラメーター応用2：弧長と体積」

最後までご覧いただきまして、ありがとうございました。

弊サイト：「スマホで独学する『学習・受験メディア』スマナビング！」では、読者の皆さんのご意見をお待ちしています。コメント欄にお寄せください。

・その他のご依頼等に付きましては、【運営元ページ】よりご連絡をお願い致します。